MATHEMATICS PAPER 2

GRADE 12

NATIONAL SENIOR CERTIFICATE

NOVERMBER 2016

INSTRUCTIONS AND INFORMATION

Read the following instructions carefully before answering the questions.

1. This question paper consists of 10 questions.
2. Answer ALL the questions in the ANSWER BOOK provided.
3. Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
4. Answers only will not necessarily be awarded full marks.
5. calculator (non-programmable and
6. You may use an approved scientific non-graphical), unless stated otherwise.
7. If necessary, round off answers to TWO decimal places, unless stated otherwise,
8. Diagrams are NOT necessarily drawn to scale.
9. Write neatly and legibly.

QUESTION 1

A survey was conducted at a local supermarket relating the distance that shoppers lived from the store to the average number of times they shopped at the store in a week. The results are shown in the table below

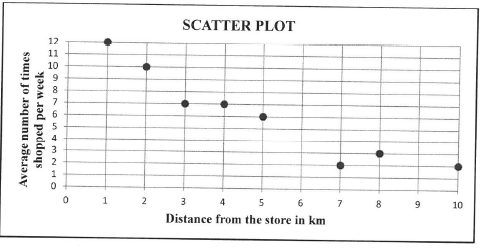
1.1 Use the scatter plot to comment on the strength of the relationship between the distance a shopper lived from the store and the average number of times she/he shopped at the store in a week.(1)

1.2 Calculate the correlation coefficient of the data. (1)

1.3 Calculate the equation of the least squares regression line of the data.(3)

1.4 Use your answer at QUESTION 1.3 to estimate the average number of times that a shopper living 6 km from the supermarket will visit the store in a week. (2)

1.5 Sketch the least squares regression line on the scatter plot provided in the ANSWER BOOK. (2) [9]

QUESTION 2

The heights of 160 learners in a school are measured. The height of the shortest learner is 1,39 m and the height of the tallest learner is 2,21 m. The heights are represented in the histogram below.

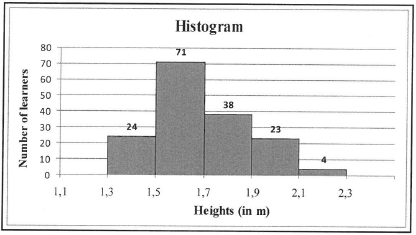
2.1 Describe the skewness of the data. (1)

2.2 Calculate the range of the heights. (2)

2.3 Complete the cumulative frequency column in the table given in the ANSWER BOOK (2)

2.4 Draw an ogive cumulative frequency curve) to represent the data on the grid provided in the ANSWER BOOK (4)

2.5 Eighty learners are less than x metres in height. Estimate x. (2)

2.6 The person taking the measurements only had a 1,5 m measuring tape available. In order to compensate for the short measuring tape, he decided to mount the tape on a wall at a height of 1 m above the ground. After recording the measurements he discovered that the tape was mounted at 1,1 m above the ground instead of 1 m.

How does this error influence the following:

2.6.1 Mean of the data set (1)

2.6.2 Standard deviation of the data set (1) [13]

QUESTION 3

In the diagram, A(-7; 2), B, C(6; 3) and D are the vertices of rectangle ABCD. The equation of AD is y = 2x + 16. Line AB cuts the y-axis at G. The x-intercept of line BC is F(p : 0) and the angle of inclination of BC with the positive x-axis is a The diagonals of the rectangle intersect at M.

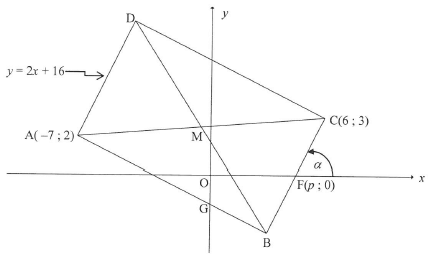
3.1 Calculate the coordinates of M. (2)

3.2 Write down the gradient of BC in terms of p.(1)

3.3 Hence, calculate the value of p.(3)

3.4 Calculate the length of DB.(3)

3.4 Calculate the size of a(2)

3.6 Calculate the size of OGB.(3)

3.7 Determine the equation of the circle passing through points D, B and C in the form (x-a)² +(y-b)² =r² (3)

3.8 If AD is shifted so that ABCD becomes a square, will BC be a tangent to the circle passing through points A, M and B, where M is now the intersection of the diagonals of the square ABCD? Motivate your answer. (2) [19]

QUESTION 4

In the diagram, M is the centre of the circle passing through T(3:7), R and S(5:2). RT is a diameter of the circle. K(a; b) is a point in the 4^th quadrant such that KTL is a tangent to the circle at T.

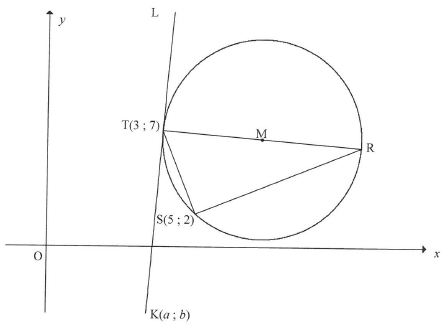
4.1 Give a reason why TSR = 90°(1)

4.2 Calculate the gradient of TS. (2) 

4.3 Determine the equation of the line SR in the form y = mx + c. (3)

4.4  The equation of the circle above is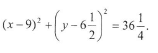 

4.4.1 Calculate the length of TR in surd form. (2)

4.4.2 Calculate the coordinates of R. (3)

4.4.3 Calculate sin R. (3)

4.4.4 Show that b = 12a - 29. (3)

4.4.5 If TK = TR, calculate the coordinates of K.(6) [23]

QUESTION 5

5.1 Given: sin 16° = p Determine the following in terms of p, without using a calculator

5.1.1 sin196° (2)

5.1.2 cos16° (2)

5.2 Given: cos(A - B) = cosAcosB + sinAsinB

Use the formula for cos(A-B) to derive a formula for sin(A + B) (3)

5.3 Simplify completely, given that 0° < A < 90° (5)

5.4 Given: cos

Determine, without using a calculator, the value of EACH of the following in its simplest form:

5.4.1 cos B (3)

5.4.2 sin B (2)

5.4.3 cos (B +45º) (4) [21]

QUESTION 6

In the diagram the graph of ƒ(x) - 2 sin 2x is drawn for the interval x ∈ (-180° : 180°).

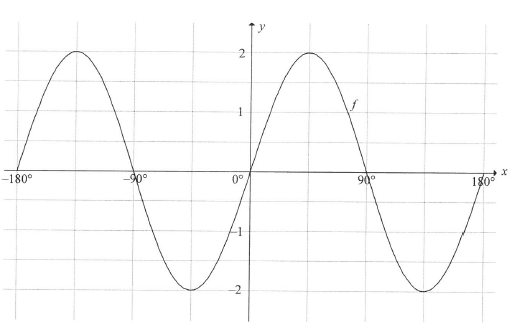
6.1 On the system of axes on which is drawn in the ANSWER BOOK, draw the graph of g(x) = -cos 2x for x∈ [-180° ; 180°). Clearly show all intercepts with the axes, the coordinates of the turning points and end points of the graph. (3)

6.2 Write down the maximum value of ƒ(x)-3. (2)

6.3 Determine the general solution of ƒ(x) = g(x). (4)

6.4 Hence, determine the values of x for which ƒ(x) < g(x) in the interval  x∈ (-180° : 0°) (3) [12]

QUESTION 7

E is the apex of a pyramid having a square base ABCD. O is the centre of the base. EBA = 0, AB = 3 m and EO, the perpendicular height of the pyramid, is x.

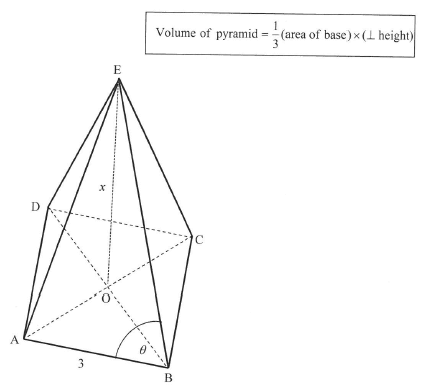
7.1 Calculate the length of OB. (3)

7.2 Show that cosθ=(5)

7.3 If the volume of the pyramid is 15 m³, calculate the value of θ. (4) [12]

Give reasons for ALL statements and calculations in QUESTIONS 8, 9 and 10.

QUESTION 8

8.1 In the diagram below PORT is a cyclic quadrilateral having RT || QP. The tangent at P meets RT produced at S. QP = QT and PTS = 70°.

8.1.1 Give a reason why P₂= 70°.

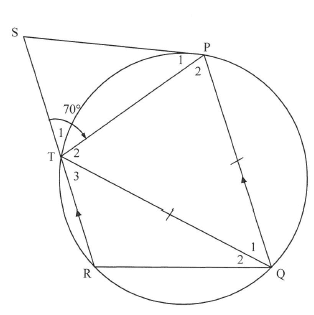(1)

8.1.2 Calculate, with reasons, the size of:

1. Q₁(3)
2. P₁ (2)

8.2 A, B and C are points on the circle having centre O. S and T are points on AC and AB respectively such that OS ⊥ AC and OT ⊥ AB. AB - 40 and AC = 48.

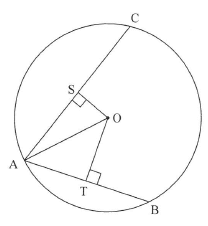
8.2.1 Calculate AT. (1)

8.2.2 If calculate the radius OA of the circle. (5) [12]

QUESTION 9

ABC is a tangent to the circle BFE at B. From C a straight line is drawn parallel to BF to meet FE produced at D. EC and BD are drawn. Ê₁ , E₂= x and Ĉ₂ = y.

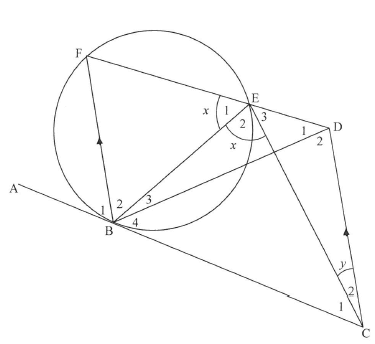
9.1 Give a reason why EACH of the following is TRUE:

9.1.1 B₁ = x (1)

9.1.2 BCD = B₁(1)

9.2 Prove that BCDE is a cyclic quadrilateral. (2)

9.3 Which TWO other angles are each equal to x? (2)

9.4 Prove that B₂=Ĉ₁ (3) [9]

QUESTION 10

10.1 In the diagram APQR is drawn. S and T are points on sides PQ and PR respectively such that ST || QR.

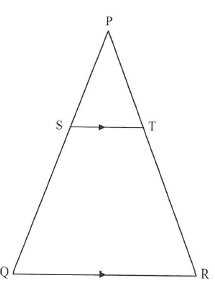
Prove the theorem which states that (6)

10.2 In the diagram HLKF is a cyclic quadrilateral. The chords HL and FK are produced to meet at M. The line through F parallel to KL meets MH produced at G. MK - X, KF - 2x, ML = y and LH=HG.

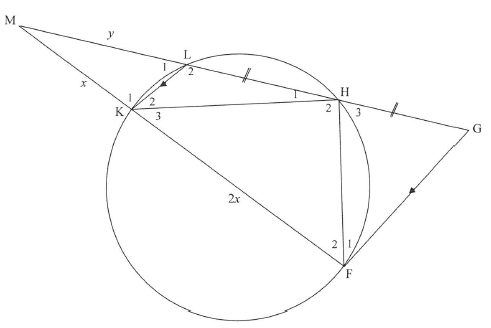
10.2.1 Give a reason why GFM = LKM.(1)

10.2.2 Prove that:

1. GH = y (3)
2. ΔMFH||| ΔMGF (5)
3. Show that (2)

10.2.3 Show that (3) [20]

TOTAL: 150