GRADE 12 MATHEMATICS PAPER 1 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 1
GRADE 12
MEMORANDUM
NOVEMBER 2016
NATIONAL SENIOR CERTIFICATE
NOTE:
• If a candidate answers a question TWICE, only mark the FIRST attempt.
• Consistent accuracy applies in all aspects of the marking memorandum.
QUESTION 1
| 1.1.1 | x(x-7)=0 x=0 or x=7 | ✓x = 0 ✓x= 7 |
| 1.1.2 | x2 -6x + 2 = 0
x = 0,35 or x= 5,65 OR x2 - 6x + 2 = 0 x2 - 6x + 9 = 2+9 (x-3)2 = 7 x-3 = ± √7 x= 0,35 or x=5,65 | ✓correct substitution into ✓(x-3)2 = 7 ✓x= 0,35 ✓x=5,65 (3) |
| 1.1.3 | √x-1 + 1 = x √x-1 = x-1 x-1 = x2 - 2x + 1 x2 - 3x + 2 = 0 (x+2)(x-1) = 0 x=2 or x=1 Both answers are valid OR OR By inspection: x-1=0 or x-1=1 x=2 or x=1
| ✓ isolate √x-1 (5) ✓ isolate √x-1 ✓ isolate √x-1 |
| 1.1.4 | 3x+3 - 3x+2 = 486 3x33-3x32=486 3x(33-32)=486 3x=27 3x=33 x=3 OR 3x+3 - 3x+2=486 3x+2(31-1) = 486 3x+2 = 35 x+2 = 5x+2 = 5 x= 3 | ✓expansion ✓3x=27 ✓x=3 (4) ✓common factor ✓(31-1) ✓3x+2=243 ✓x+3 (4) |
| 1.2.1 | ƒ(x) = x2 + 3x - 4 0=(x+4)(x+1) x=-4 or x=1 | ✓factors ✓both answers (2) |
| 1.2.2 | x2 + 3x - 4 < 0 (x+4)(x-1) < 0 -4 < x< 1 OR X∈(-4;1) | ✓✓-4 < x< 1 (2) |
| 1.2.3 | 2x+3≥0 x≥-3/2 ƒ(x)≥0 when ƒ is increasing The turning point occurs at x = (-4+1)/2 x≥-3/2 | ✓2x+3 ✓x≥-3/2 (2) ✓x = (-4+1)/2 ✓x≥-3/2 (2) |
| 1.3 | x=2y and x2 - 5xy = -24 (2y)2 - 5(2y)(y) = -24 4y2-10y2=-24 -6y2 = -24 y2=4 y=-2 or y=2 x=-4 or x=4 OR OR | ✓substitution of 2y ✓ substitution of x/2 ✓ equating x=x2+24 |
| [24] |
QUESTION 2
| 2.1 | T4=-7 | ✓-7 (1) |
| 2.2 | Tn = a+(n-1)d -87=5+(n-1)(-4) -87=5-4n+4 4n=96 n=24 OR -4n+9=-87 -4n=-96 n=24 | ✓a=5 and d=-4 ✓-87 = 5+(n-1)(-4) ✓n=24 (3) ✓-4n+9 ✓-4n+9=-87 ✓n=24 (3) |
| 2.3 | -3;-7......;-87 OR OR All negative terms can be written down and added to get the answer of –990 OR | ✓n=22 ✓a=-3 ✓answer (3) ✓n=22 ✓a=-3 ✓answer(3) ✓a=-3 answer(3) ✓ ✓-6 ✓answer(3) |
| 2.4 | 5;-15;-35...... d=-20 tn=-20n +25 Last term in the sequence divisible by 5 is: -4187+4(3) =-4175 Tn =-20n+25 -4175 =-20n+25 20n=4200 n=210 There will be 210 terms in the sequence that is divisible by 5. OR 5 ; 1 ; –3 ; ... ; –83 ; –87; ……; – 4187 Tn=-4n+9 -4187 =-4n+9 4n=4196 n=1049 There are 1049 terms in the sequence T1;T6;T11;T16 are divisible by 5 The largest integer value of k such that 5k-4≤1049 5k ≤ 1053 k≤210.6 k=210 OR 5 ; 1 –3 ; –7 ; … ; –4175; –4179 ;–4183 ; –4187 Tn=a+(n-1)d -4175 = 5+(n-1)(-4) -4180 = -4(n-1) n=1046 Number of terms divisible by 5 =1046 - 1 +1 =210 | ✓d=-20 ✓Tn=-20n+25 ✓-4175 =-20n+25 ✓n=210 (4) ✓-4n+9=-4187 ✓n=1049 ✓5k-4 ≤1049 ✓k=210 (4) ✓d=-4 ✓-4175=-4n+9 ✓1046 ✓n=210 (4) [11] |
QUESTION3
3.1.1 | – 1 ; x ; 3 ; x + 8 ; ... - 2x + 2 = 2x + 2 4x = 0 x = 0 | ✓x + 1; 3 - x and x ✓calculating second differences ✓- 2x + 2 = 2x + 2
✓x = 0(4) |
3.1.2 | First differences 1 ; 3 ; 5 ; …… Sn = n [2(1) + (n - 1)(2)] 2 = n2 250 < n 2 n > √ 250 ∴ n > 15,8 The sum of the 16 first differences will be greater than 250. Therefore the 17th term of the quadratic number pattern is the first satisfying this condition. | ✓S = n 2 ✓Sn > 250 ✓n > 15,8 ✓n = 17(4) |
3.2.1 | 21 + 21(0,85) + 21(0,85)2 + ......... T = ar n-1 n T = (21)(0,85)9 = 4,86 cm | ✓n = 10 ; r = 0,85 or 17 20 ✓substitution into correct formula ✓answer (3) |
3.2.2 | Sn a(1 - r n ) 1 - r S15= 21(1 - (0,85)15 ) 1 - 0,85 = 127,77 Area of the page = 30 x 21 = 630 Percentage of paper covered in grey ink: = 127,77 x 100% 630 = 20,28% | ✓n = 15 ✓127,77 ✓630 ✓20,28 (4) [15] |
QUESTION 4
4.1 | y = 0 | ✓y = 0 (1) |
4.2 | R(0 ; 1) | ✓answer (1) |
4.3 | y = ax 9 = a2 ∴ a = 3 | ✓substitution ✓a = 3 (2) |
4.4 | DP = 2 – b y = 3x 1 = 3b 81 3-4 = 3b b = - 4 DP = 2 - (-4) = 6 units | ✓1 = 3b 81 ✓3-4 or use of logs ✓b = - 4 ✓DP = 6 units (4) |
4.5 | h(x + 2) + k = 0 h(x + 2) = -k 0 < -k < 1 81 - 1 < k < 0 81 | ✓✓- k < 1 or k > - 1 81 81 ✓- 1 < k < 0 81 (3) [11] |
QUESTION 5
5.1 | f (x) = -x 2 + 4x - 3 f '(x) = 0 or x = - 4 2(- 1) - 2x + 4 = 0 x = 2 x = 2 y = -(2)2 + 4(2) - 3 = 1 B(2 ; 1) OR - x 2 + 4x - 3 = 0 x 2 - 4x + 3 = 0 (x - 3)(x - 1) = 0 x = 3 or x = 1 x = 3 + 1 2 x = 2 y = -(2)2 + 4(2) - 3 = 1 B(2 ; 1) | ✓- 2x + 4 = 0 or x = - 4 2(-1) ✓y = -(2)2 + 4(2)-3 (2) ✓x = 3 +1 2
✓y = -(2)2 +4(2)-3 (2) |
5.2 | Range: y ≤ 1 OR Range: y ∈ (-∞ ; 1] | ✓y ≤ 1 (1) ✓(-∞ ; 1] (1) |
5.3 | x ≤ -1 or x > 2 OR ( -∞; -1]∪(2 ;-∞) | ✓critical values ✓x ≤-1 or x>2 (2) ✓critical values ✓x ≤-1 or x>2 (2) |
5.4 | (x - p) (y + t ) = 3 Vertical asymptote of h(x) at x = 2 Translation 4 units to the left x = 2 – 4 = –2 is the equation of the vertical asymptote of h(x + 4) OR | ✓x = -2 (1) |
h(x) = 3 + 1 x - 2 + 4 = 3 + 1 x + 2 x = -2 is the equation of the vertical asymptote | ✓x = -2 (1) | |
5.5 | (x - p)(y + t ) = 3 (y + t ) = 3 - t x - p y = 3 - t x - p B(2 ;1) Point of intersection of the asymptotes p = 2 - t = 1 t = -1 | ✓ 3 x - p ✓- t ✓p = 2 ✓t = -1 (4) |
5.6 | x-intercepts of f : x 2 - 4x + 3 = 0 (x - 3)(x -1) = 0 x = 1 or x = 3 g / (x) < 0 for x ∈ R ; x ≠ 2 Hence f (x) < 0 x ≤ 1 or x ≥ 3 OR (- ∞ ; 1]∪[3 ; ∞) | ✓both critical values ✓x ≤ 1 ✓or ✓x ≥ 3 (4) [14] |
QUESTION6
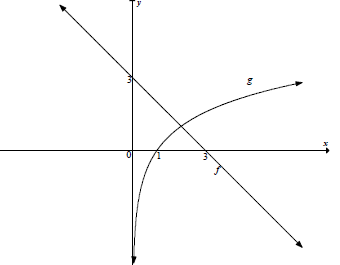
| 6.1 | | g ✓shape: increasing curve ✓(1 ; 0): only on log graph f: ✓(3 ; 0) ✓(0 ; 3)(4) | |
6.2 | y = log2 x g -1 : x = log2 y y = 2x | ✓interchange x and y ✓y = 2 x (2)
| |
6.3 | log2 (3 - x) = x 2 x = 3 - x 2 x = -x + 3 Reflect the graph of g about the line y = x to obtain g -1 and determine the point of intersection of f and g -1 | ✓✓2x = -x + 3 ✓point of intersection of f and g -1 (3) | |
6.4 | x = 1 | ✓answer(1)[10] | |
QUESTION 7
7.1 | A = P(1 + i )n | ?substituting i and values in correct formula ? answer(2) |
7.2 |  | ✓i = 0,15 12 ✓n = 46 ✓substitution into correct formula ✓answer(4) ✓i = 0,15 12 ✓n = 46 ✓substitution into correct formula ✓answer (4) |
7.3 | 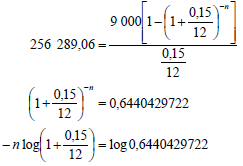 n = 35,41872568 months ∴ 36 payments are required ∴Thabiso will pay his loan off 10 months sooner OR | ✓x = 9 000 ✓substitute into correct formula ✓use of logs ✓n =35,42 ✓10 months (5) |
n = 35,41872568 ∴ 36 payments are required ∴Thabiso will pay his loan off 10 months sooner. | ✓9 000 ✓substitute into correct formula ✓use of logs ✓n =35,42 ✓10 months (5) | |
7.4 | The balance of his loan after the 35th payment was made: OR  OR | (4) |
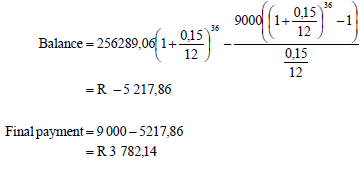 | 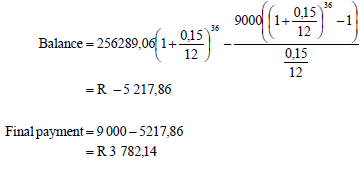 ✓✓✓✓ (4) [15] |
QUESTION 8
8.1 | f (x + h) = 3(x + h) 2 = 3(x 2 + 2xh + h 2 ) = 3 x 2 + 6xh + 3h 2 f (x + h) - f (x) = 3 x 2 + 6xh + 3h 2 - 3x 2 = 6xh + 3h 2 OR | 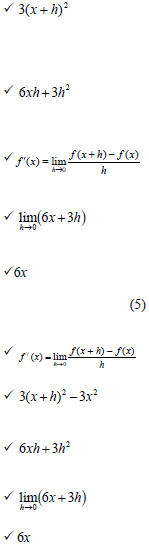 (5) |
8.2 | ✓answer ✓answer (2) | |
8.3 | 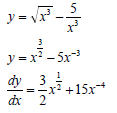 | 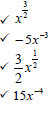 (4) |
8.4 | f (x) = x3 + ax2 + bx +18 f / (x) = 3x2 + 2ax + b At x = 1, mtan = -8 f / (1) = -8 3(1)2 + 2a(1) + b = -8 3 + 2a + b = -8 2a + b = -11........... (1) y = f (1) = g(1) = -8(1) + 20 = 12 1 + a + b + 18 = 12 a + b = -7............ (2) a = -4 b = -3 | ✓3x2 + 2ax + b ✓f / (1) = -8 or 3(1)2 + 2a(1)+ b = -8 ✓1+ a + b +18 = 12 ✓a = -4 ✓b = -3 (5) [16] |
QUESTION 9
9.1 | f'(x) = 3x2 + 8x - 3 = 0 (3x - 1)(x + 3) = 0 x = 1 or x = -3 3 | ✓equating derivative to zero ✓factors ✓x – values (3) |
9.2 | f // (x) = 6x + 8 6x + 8 < 0 x < - 4 3 OR | ✓6x + 8 ✓✓x < - 4 3
(3) |
9.3 | x ≤ -3 or x ≥ 1 3 OR | ✓x ≤ -3 ✓x ≥ 1 3 (2) ✓[-∞;-3] ✓ |
9.4 | f (0) = -18 d = -18 f (x) = ax3 + bx 2 + cx -18 f'(x) = 3ax 2 + 2bx + c f'(x) = 3x 2 + 8x - 3 3a = 3 2b = 8 a = 1 b = 4 c = -3 f (x) = x3 + 4x 2 - 3x -18 OR f'(x) = 3x2 + 8x - 3 By integration f (x) = x3 + 4x 2 - 3x + d f (0) = d = -18 a = 1 b = 4 c = -3 | ✓d = -18 ✓f '(x) = 3ax2 + 2bx + c ✓a = 1 ✓b = 4 ✓c = –3 (5) ✓f (x) = x3 + 4x2 - 3x + d ✓d = -18 ✓a = 1 ✓b = 4 ✓c = –3 (5) |
[13] |
QUESTION 10
10.1 | M(t ) = -t 3 + 3t 2 + 72t M(3) = -(3)3 + 3(3)2 + 72(3) = 216 216 molecules | M(3) = ✓-(3)3+3(3)2+72(3) ✓216 (2) |
10.2 | M (t ) = -t 3 + 3t 2 + 72t M / (t ) = -3t 2 + 6t + 72 M / (2) = -3(2)2 + 6(2) + 72 = 72 72 molecules per hour | ✓M/ (t ) = -3t 2 + 6t + 72 ✓M/ (2) ✓72 (3) |
10.3 | M (t ) = -t3 + 3t 2 + 72t M /(t) = -3t 2 + 6t + 72 M // (t) = 0 - 6t + 6 = 0 t = 1 Maximum rate of change of the number of molecules of the drug in the bloodstream is after 1 hour | ✓M// (t ) ✓M // (t ) = 0 ✓answer (3) [8] |
QUESTION 11
11.1 | ✓a = 20 ✓b = 128(2) | |||
Watches TV during exams
| Do not watch TV during exams | |||
Male | 80 | a | ||
Female | 48 | 12 | ||
Total | b | 32 | ||
a +12 = 32 a = 20 b = 80 + 48 = 128 | ||||
11.2 | No P(M and not watching TV) = 20 ≠0 160 | ✓No ✓reason(2) | ||
11.3.1 | P(watching TV) = 128 = 4 = 0,8 = 80% 160 5 | ✓128 ✓160(2) | ||
11.3.2 | P(female and not watching TV) = 12 = 3 = 0,075 = 7,5% 160 40 | ✓12 ✓160 (2) [8] | ||
QUESTION 12
12. | We want to create codes that are even numbers greater than 5000. The digit 6 can be used in one of two places in these codes and therefore this presents two scenarios. CASE 1: The first digit is a 6. 6 2 4 1 × 5 × 4 × 2 Number of codes starting with 6. = 1 × 5 × 4 ×2 = 40 CASE 2: The first digit is a 5 or 7 5 2 7 4 6 2 × 5 × 4 × 3 Number of codes not starting with 6. begin = 2 × 5 × 4 ×3 = 120 Therefore total number of possible codes.= 40 + 120 = 160. OR (3 ´ 5 ´ 4 ´1) + (3 ´ 5 ´ 4 ´1) + (2 ´ 5 ´ 4 ´1) = 60 + 60 + 40 = 160 OR (3 ´ 5 ´ 4 ´ 3) - (1´ 5 ´ 4 ´1) = 180 - 20 = 160 | ✓1 × 5 × 4 ×2 ✓40 ✓2 × 5 × 4 ×3 ✓120 ✓160 [5] ✓(3×5×4×1) ✓(3×5×4×1) ✓(2×5×4×1) ✓160 [5] ✓(3×5×4×3) ✓(1×5×4×1) ✓160 [5]
|
TOTAL | 150 |
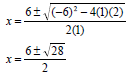
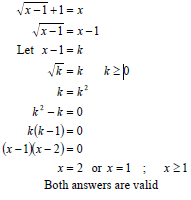
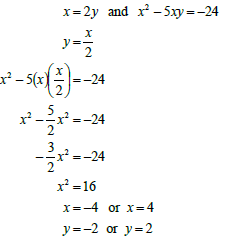
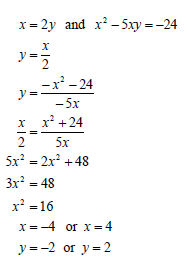
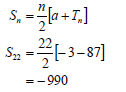
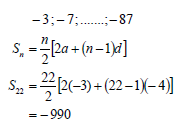
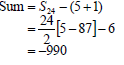
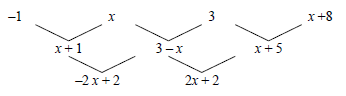
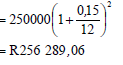
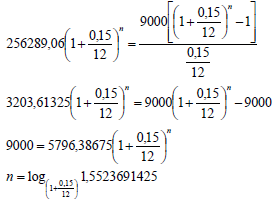
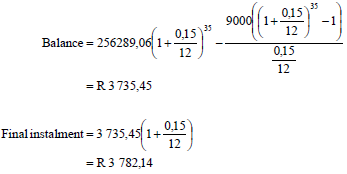
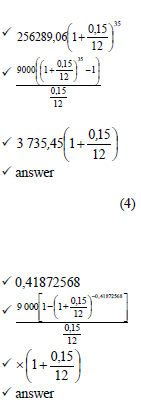
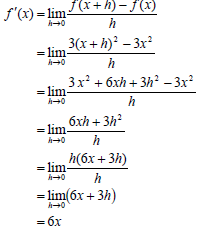
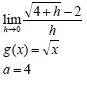
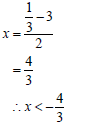
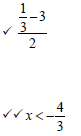 (3)
(3)