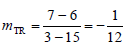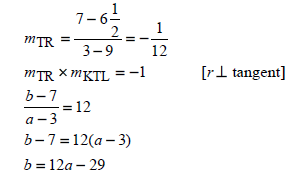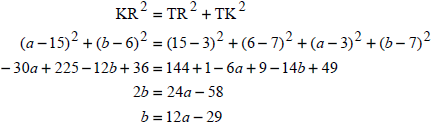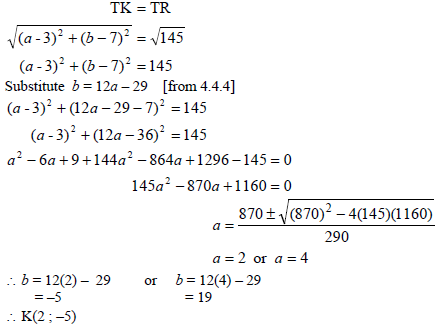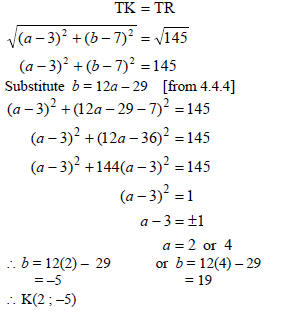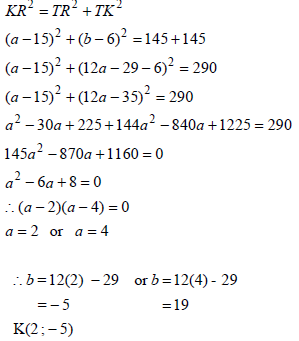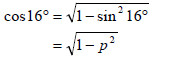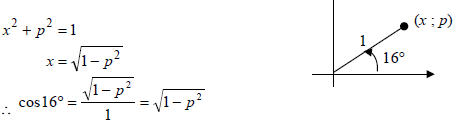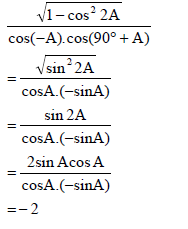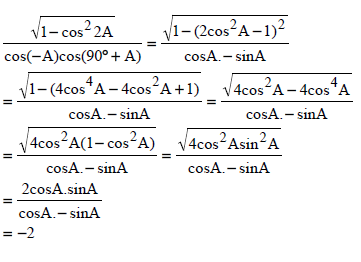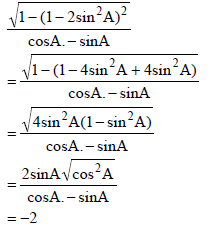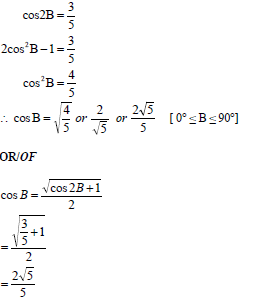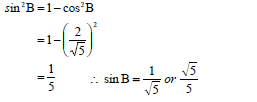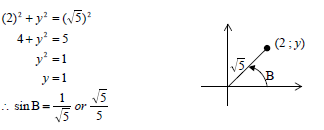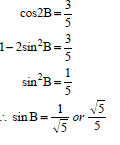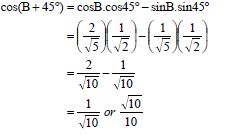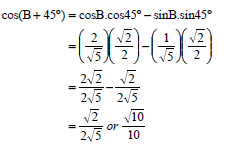GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 2
GRADE 12
MEMORANDUM
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2016
NOTE:
- If a candidate answered a question TWICE, mark only the FIRST
- If a candidate has crossed out an attempt to answer a question and did not redo it, mark the crossed-out version.
- Consistent accuracy applies in ALL aspects of the marking memorandum. Stop marking at the second calculation
- Assuming answers/values in order to solve a problem is NOT
QUESTION 1
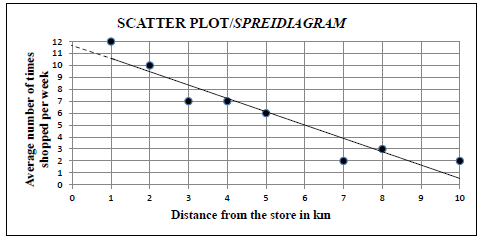
Distance from the store in km | 1 | 2 | 3 | 4 | 5 | 7 | 8 | 10 |
Average number of times shopped per week | 12 | 10 | 7 | 7 | 6 | 2 | 3 | 2 |
1.1 | Strong | ? (1) |
1.2 | –0,95 (–0,9462..) | ? (1) |
1.3 | a = 11,71 (11,7132…) b = –1,12 (–1,1176…) yˆ = -1,12x + 11,71 | ? value of a ? value of b ? equation (3) |
1.4 | yˆ = -1,12(6) + 11,71 = 5 times | ? substitition ? answer (2) |
1.5 | On scatter plot | ?? A line close to any 2 of the following points: (5 ; 6) or (10 ;½ ) or (6 ; 5) or (0 ; 11,7) (2) [9] |
QUESTION 2
2.1 | Positively skewed OR skewed to the right | ? answer (1) | ||||
2.2 | Rangeg = 2,21 – 1,39 = 0,82 m | ? subtract values ?answer (2) | ||||
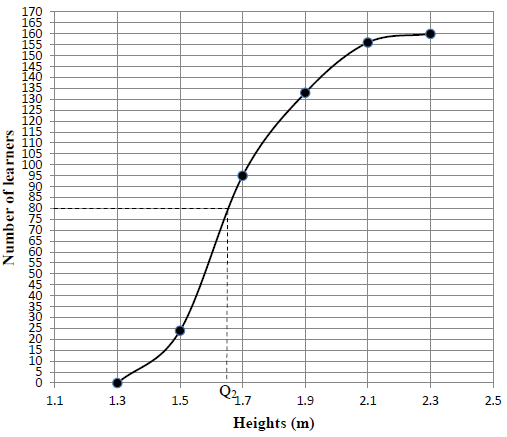
2.3 | ?95 , 133, 156 ?160 (2) | |||||
Intervals | Cumulative frequency | |||||
1,3 ≤ x < 1,5 | 24 | |||||
1,5 ≤x < 1,7 | 95 | |||||
1,7 ≤ x < 1,9 | 133 | |||||
1,9 ≤ x < 2,1 | 156 | |||||
2,1 ≤ x < 2,3 | 160 | |||||
2.4 | OGIVE | ? upper limits ? cum f ? shape ? grounded (4) | ||||
2.5 | method (using 80 to determine the height) 1,65 (accept any value between 1,6 and 1,69) | ? method ? answer (2) | ||||
2.6.1 | The mean would change by 0,1 m | ? answer (1) | ||||
2.6.2 | No influence/change as there is no difference in variation of data. | ? answer (1) [13] | ||||
QUESTION 3
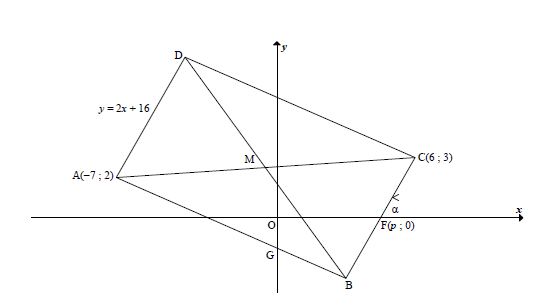
3.1 | M = Midpt of AC [diags of rectangle bisect/] | ? x-value of M ? y-value of M (2) |
3.2 | m BC = 3 - 0 = 3 6 - p 6 - p OR mBC = 0 - 3 = - 3 p - 6 p - 6 | ?answer (1) ?answer (1) |
3.3 | mAD = mBC [AD | | BC] mBC = 2 3 = 2 6 - p 3 = 12 - 2 p p = 4½ OR y - y1 = 2(x - x1) C(6 ;3) y - 3 = 2(x - 6) ∴ y = 2x - 9 but y = 0 ∴ x = 4½ = p OR | ? mBC = 2 ? equating ?answer (3) ? mBC = 2 ? substituting (6 ; 3) ?answer (3) |
y = 2x + c 3 = 12 + c - 9 = c y = 2x - 9 0 = 2x - 9 x = 9 ∴ p = 9 2 2 | ? mBC = 2
? substituting ?answer (3) | |
3.4 | DB =AC [diag of rectangle = ] AC = √170 \ DB = 170 or 13,04 | ? substitution ? length of AC ? AC = BD (3) |
3.5 | tan a = mBC = 2 ∴ a = 63,43° | ? tan a = mBC ? a = 63,43° (2) |
3.6 | In quadrilateral OFBG: OFˆB = 63,43° [vert opp ∠s] FOˆ G = GBˆ F = 90° ∴ OGˆ B = 360° -[90° + 90° + 63,43°] [sum ∠s quad = 360°] ∴ OGˆ B = 116,57° OR mAB = -½ 90° + OGˆ A = 153,43° ∴ OGˆ A = 63,43° OGˆ B = 180° – 63,43° = 116,57° OR FOˆG = GBˆ F = 90° ∴ GOFB is cyc quad OGˆ B = 180° – 63,43° [∠s of cyc quad = 180°] = 116,57° OR OFˆB = 63,43° XOˆ G = FBˆ G = 90° ∴OGBF is a cyclic quad ∴ OGˆ B = 180° - 63,43° OGˆ B = 116,57° | ? size of OFˆB ? S ? answer (3) ? m = - ½ ? S ? answer (3)
? S ? S ? answer (3) ? S ? S ? answer (3) |
3.7 |
[BD is diameter] | ? M is centre
? r = √170 2
? equation (3) |
3.8 | CBˆ M = BAˆ M = 45° [diag of square bisect ∠s] ∴BC will be a tangent [converse tan chord th] OR 
| ?S ? R (2) ?S ? R (2) [19] |
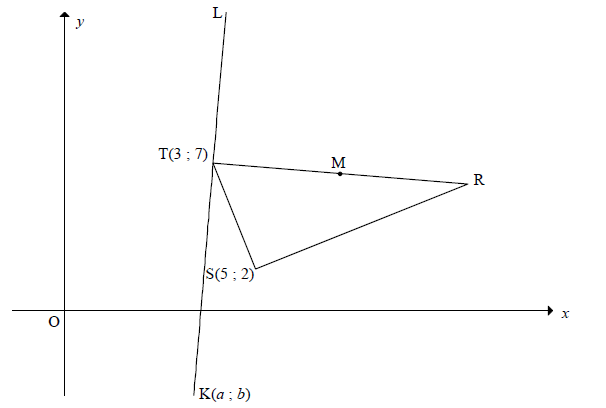
QUESTION 4
4.1 | ∠ in semi circle/ ∠ at centre = 2Ð on circle | ? R (1) |
4.2 | mTS = 7 - 2 3 - 5 = - 5 2 | ? substitution ? mTS (2) |
4.3 | mTS x mRS = -1 [TS ⊥ SR] mRS = 2 5 y = 2 x + c 5 2 = 2 (5) + c 5 c = 0 y = 2 x 5 OR | ? mRS
?substitution m and (5 ; 2)
? equation (3) |
mTS ´ mRS = -1 [TS ⊥ SR] ∴ mRS = 2 5 y - y1 = 2 (x - x1) 5 y - 2 = 2 (x - 5) 5 y = 2 x 5 | ? mRS
?substitution m and (5 ; 2) ? equation (3) | |
| 4.4.1 | 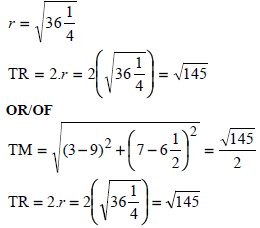 | ? r ? answer (2) ? substitution ? answer (2) |
| 4.4.2 | OR Answer only: full marks Answer only: only 1 coordinate correct (1 mark) | ? M ? x coordinate ? y coordinate(3) M ? x coordinate ? y coordinate (3) |
mTM = 9 - 3 = - 1 6 ½ - 7 12 TM : 7 = - 1 (3) + c y = - 1 x + 29....(1) 12 12 4 SR : y = 2 x............. (2) 5 2 x = - 1 x + 29 5 12 4 29 x = 29 60 4 ∴ x = 15 ∴ y = 2 (15) = 6 5 | ? Equating ? x coordinate ? y coordinate(3) | |
| 4.4.3 | ST = OR | ? substitution ? answer ? ratio (3) ? area ? rule ? ratio (3) |
| 4.4.4 | OR OR OR | ?mTR =-½ ?mKTL = 12 ?y=12x - 29 (3) ?mTR =-½ ?mKTL = 12 ?substitution (3;7)&(a;b) (3) ?subst into Pyth ?multiplication ?simplification (3) |
| 4.4.5 | OR OR | ?substitution into disctance formula ?substitution of b=12a-29 ?standard form ?subst into formula or factorise ?values of a ?values of b (6) ?substitution into disctance formula ?substitution of b=12a-29 ?(a-3)2 =1 ?±1 ?values of a ?values of b (6) ?substitution ?substitution of b=12a-29 ?standard form ?factors ?values of a ?values of b (6) [23] |
QUESTION 5
5.1.1 | sin196° = - sin16° = - p | ?reduction ?answer (2) |
5.1.2 | OR | ?statement ?answer (2) ?x in terms of p ?answer (2) |
5.2 | sin(A + B) = cos[90° - (A + B)] = cos[(90° - A) - B] = cos(90° - A)cosB + sin(90° - A)sinB = sin AcosB + cos AsinB | ?co-ratio ?correct form ?expansion (3) |
5.3 | OR OR
|
? √sin2 2A ? cosA ? - sinA ? 2sinAcosA ? answer (5) ? 2 cos2 A -1 ? cosA ? - sinA ?identity ? answer (5) ?1-2sin2A ?cosA ?- sinA ? identity ? answer (5) |
| 5.4.1 | ? identity ? value of cos2B ? answer ? = √cos 2B + 1 2 ? value of cos2B ? answer (3) | |
| 5.4.2 | OR OR | ? sin2B = 1 5 ? answer (2) ? y = 1 ? answer (2) ? sin2B = 1 5 ? answer (2) |
| 5.43 | OR | 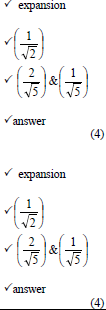 [21] |
QUESTION 6
| 6.1 | 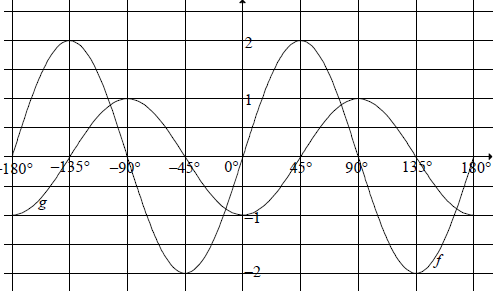 | ? x- intercepts/ ? y- intercept/ ? turning pts/ (3) |
| 6.2 | f (x) - 3 = 2 sin 2x - 3 ∴ maximum value = 2 – 3 = –1 | ? ? answer (2) |
| 6.3 | 2 sin 2x = - cos 2x tan 2x = - ½ ref∠ = 26,57° 2x = 153,43° + k.180°; k ∈ Z x = 76,72° + k.90°; k ∈ Z or x = -13.28° + k.90°, k ∈ Z OR 2 sin 2x = - cos 2x tan 2x = - ½ ref ∠= 26,57° 2x = 153,43° + k.360° or 333,43° + k.360°, k ∈ Z x = 76,72° + k.180° or 166,72° + k.180° ; k ∈ Z | ? tan 2x = - ½
or – 26,56o ? 76,72° or -13,28o ? k.90°; k ∈ Z (4) ? tan 2x = - ½ ? 2x = 153,43° &333,43° ? 76,72° &166,72o ? k.180°; k ∈ Z (4) |
| 6.4 | x ∈ (-103,28°; - 13,28°) OR –103,28° < x < –13,28° | ?? values ?notation(3) ?? values ?notation (3) [12] |
QUESTION 7
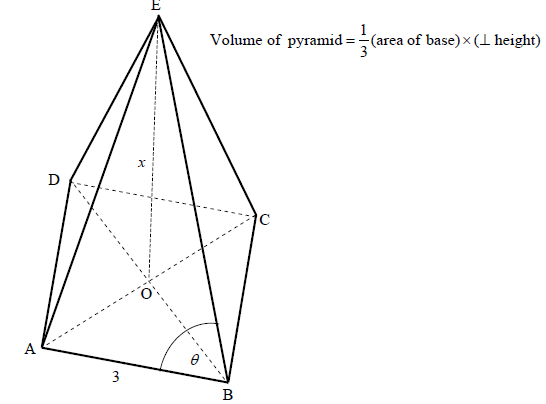
7.1 | 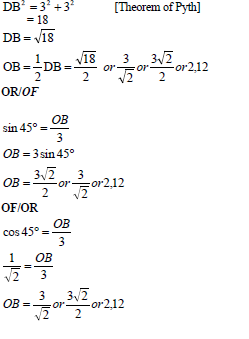 | ? substitution into Pyth ? value of DB ? answer (3) ? correct ratio ? OB as subject ? answer (3) ? correct ratio ? special angle ? answer (3) |
OR AOB = 90º (diagonals bisect ⊥) OB=OA AB2 = AO2 + BO2 [pyth] ∴AB2 = 2OB2 2OB2=32 | ? OB = OA ? Pyth ? answer (3) | |
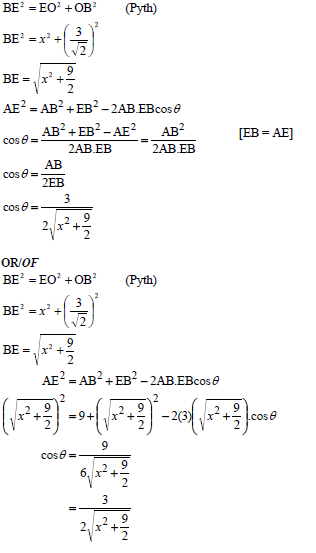
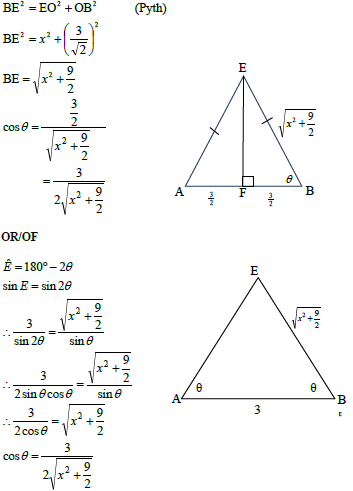
7.2 | OR
| ? substitution into Pyth ? length of BE ?correct cosine rule ? cos θ as subject ? simplification (5) ? substitution into Pyth ? length of BE ?correct cosine rule ? substituting ? cos θ as subject (5) ? substitution into Pyth ? length of BE ?sketch with values ? 3/2 ?substitution (5) ?E = 180º - 2θ ?sinE = sin2θ ?subst into sine rule ?diagram ?2sinθcosθ (5) |
| 7.3 | 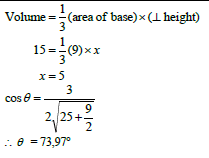 | ? substitution ? x-value ? substitution ? answer (4) [12] |
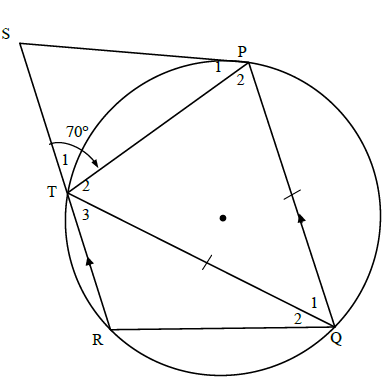
QUESTION 8
8.1.1 | Alternate angles PQ || SR | ? R (1) |
8.1.2(a) | Tˆ2 = 70° [∠s opp = sides] ∴Qˆ1 = 180° - 2(70°) [∠s/e Δ = 180°] = 40° | ? S ?R ? answer (3) |
8.1.2(b) | Pˆ1 = 40° [tangent chord th] | ? S ?R (2) |
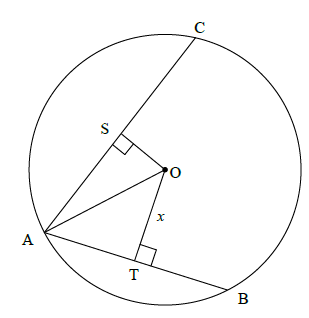
8.2
8.2.1 | AT = 20 [line from centre ⊥ to chord] | ?S(1) |
8.2.2 | OR Let OS = 7, then OT = 15 In ΔAOT: AO2 = 202 + 152 = 625 AO = 25 In ΔAOS: AO2 = 242 + 72 = 625 AO = 25 ∴ OA = 25 OR AO2 = OS2 + AS2 [Pyth : ΔAOS] OT 2 + AT2 = OS2 + AS2 [Pyth : ΔAOT] Let OT = 15x. Then OS = 7x But AS = 24 [line from centre ^ to chord] (15x)2 + 400 = (7x)2 + 576 225x2 + 400 = 49x2 + 576 176x2 = 176 x = 1 ∴AO =√225 + 400 = 25 | ? equating ? AS = 24 ? substitution OS = 7/15OT ? OT ? radius (5) ?? testing in ΔAOT ?? testing in ΔAOS ?conclusion (5) ?equating ?AS=24 ?substitution ?x=1 ?radius (5) ?AS=24 ?substitution OS=7/15OT ?equating ?subst pyth ?radius (5) [12] |
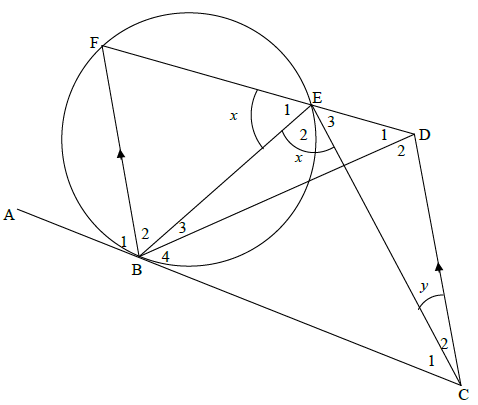
QUESTION 9
9.1.1 | tangent chord theorem | ? R (1) |
9.1.2 | corresponding ∠s/e; FB || DC | ? R (1) |
9.2 | Eˆ1 = BCˆ D ∴ BCDE = cyclic quad [converse ext ∠ cyc quad] | ? S ? R (2) |
9.3 | Dˆ2 = Eˆ2 [∠s in the same segment] Dˆ2 = FBˆ D [alt ∠s, BF ||CD||CD] | ? S ? S (2) |
9.4 | Bˆ 3 = y OR Bˆ3 = Cˆ2 [∠s in the same segment] Bˆ2 = x - y OR Bˆ3 + Bˆ2 = x [from 9.3 and 9.4] Cˆ1 = x - y [from 9.2 and 9.3] ∴Bˆ 2 = Cˆ1 OR In Δ BFE and D BEC Eˆ1 = Eˆ2 [= x] Fˆ = Bˆ3 + Bˆ4 [tan - chord theorem] ∴ΔDBFE///DCBE [∠,∠,∠] ∴Bˆ 2 = Cˆ1 | ? S ? S ? S (3) ? identifying Δ ’s ? S ? S (3) [9] |
QUESTION 10
10.1 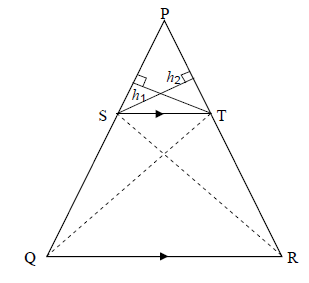
10.1 | Constr : Join S to R and T to Q and draw h1 from S ⊥ PT and h2 from T ⊥ PS | ? constr (6) |
Proof : |
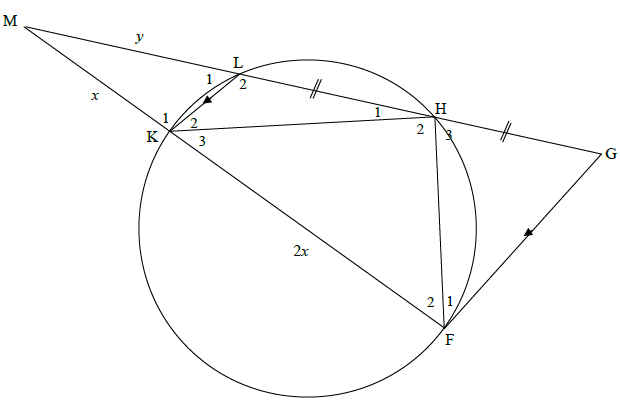
10.2
| 10.2.1 | Corresponding ∠s/e; GF || LK | ? R (1) |
| 10.2.2(a) | GL = FK OR GL = 2x [prop theorem; GF | | LK] LM KM y x 2GH = 2x [LH = HG] y x ∴GH = y | ?S ? R ? GL = 2GH (3) |
10.2.2(b) | K1 = GFM [corresponding∠s; GF || LK] LKM or → K1 = MHˆ F [ext ∠cyclic quad] MHˆF = GFM In ΔMFH and ΔMGF: Mˆ = Mˆ [common] MHˆF = GFˆM [proven] ∴ΔMFH | | | ΔMGF [∠∠∠] OR K1 = GFˆM [corresponding∠s; GF || LK] LKˆM or K1 = MHˆF [ext ∠cyclic quad] MHˆF = GFˆM In ΔMFH and ΔMGF: Mˆ = Mˆ [common] MHˆF = GFˆM [proven] Fˆ2 = Gˆ [∠s of Δ = 180°] ∴ΔMFH | | | ΔMGF | ?S ? R ? S ? S ? R (5) ?S ? R ? S ? S ? S (5) |
10.2.2(c) | ∴GF = MF [ ||| Δs] FH MH = 3x 2y | ?S ?R (2) |
10.2.3 | MF = MG [ ||| Δs] MH MF 3x = 3y [from 10.2.2(c)] 2y 3x 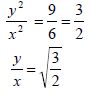
| ? S ?substitution ? simplificatio n (3) [20] |
TOTAL MARKS | 150 |
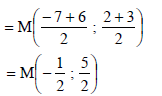
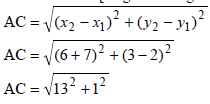
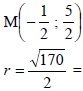 M is the centre
M is the centre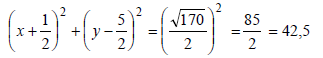
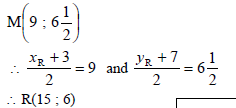
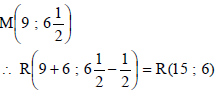
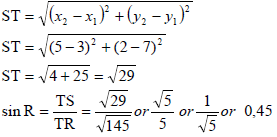
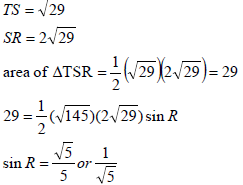
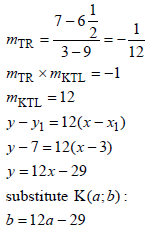 [R⊥tangent]
[R⊥tangent]