PHYSICAL SCIENCES PHYSICS PAPER 1 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupPHYSICAL SCIENCES (PHYSICS)
PAPER ONE (P1)
GRADE 12
NSC EXAM PAPERS AND MEMOS
NOVEMBER 2016
INSTRUCTIONS AND INFORMATION
- Write your centre number and examination number in the appropriate spaces on the ANSWER BOOK.
- This question paper consists of 10 questions. Answer ALL the questions in the ANSWER BOOK.
- Start EACH question on a NEW page in the ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Leave ONE line between two subquestions, for example between QUESTION 2.1 and QUESTION 2.2.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- You are advised to use the attached DATA SHEETS.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your final numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions et cetera where required.
- Write neatly and legibly.
QUESTIONS
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Write down the question number (1.1–1.10), choose the answer and make a cross (X) over the letter (A–D) of your choice in the ANSWER BOOK.
EXAMPLE: ![]()
1.11
1.1 The tendency of an object to remain at rest or to continue in its uniform motion in a straight line is known as …
- inertia.
- acceleration.
- Newton's Third Law.
- Newton's Second Law. (2)
1.2 The mass of an astronaut on Earth is M. At a height equal to twice the radius of the Earth, the mass of the astronaut will be …
- ¼M
- 1/9M
- M
- 2M (2)
1.3 An object is thrown vertically upwards from the ground.
Which ONE of the following is CORRECT regarding the direction of the acceleration of the object as it moves upwards and then downwards? Ignore the effects of air resistance. (2)
OBJECT MOVING UPWARDS | OBJECT MOVING DOWNWARDS | |
A | Downwards | Upwards |
B | Upwards | Downwards |
C | Downwards | Downwards |
D | Upwards | Upwards |
1.4 A person drops a glass bottle onto a concrete floor from a certain height and the bottle breaks. The person then drops a second, identical glass bottle from the same height onto a thick, woollen carpet, but the bottle does not break.
Which ONE of the following is CORRECT for the second bottle compared to the first bottle for the same momentum change? (2)
AVERAGE FORCE ON SECOND BOTTLE | TIME OF CONTACT WITH CARPET | |
A | Larger | Smaller |
B | Smaller | Smaller |
C | Larger | Larger |
D | Smaller | Larger |
1.5 A block of mass m is released from rest from the top of a frictionless inclined plane QR, as shown below.
The total mechanical energy of the block is EQ at point Q and ER at point R. The kinetic energy of the block at points Q and R is KQ and KR respectively. 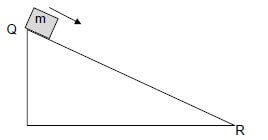
Which ONE of the statements regarding the total mechanical energy and the kinetic energy of the block at points Q and R respectively is CORRECT? (2)
TOTAL MECHANICAL ENERGY E | KINETIC ENERGY K | |
A | EQ > ER | KQ = KR |
B | EQ = ER | KQ < KR |
C | EQ = ER | KQ = KR |
D | EQ < ER | KQ > KR |
1.6 The diagram below shows the positions of two stationary listeners, P and Q, relative to a car moving at a constant velocity towards listener Q. The hooter on the car emits sound. Listeners P and Q and the driver all hear the sound of the hooter.
Which ONE of the following CORRECTLY describes the frequency of the sound heard by P and Q, compared to that heard by the driver? (2)
FREQUENCY OF THE SOUND HEARD BY P | FREQUENCY OF THE SOUND HEARD BY Q | |
A | Lower | Higher |
B | Higher | Higher |
C | Lower | Lower |
D | Higher | Lower |
1.7 Two charges, + Q and – Q, are placed a distance d from a negative charge – q. The charges, + Q and – Q, are located along lines that are perpendicular to each other as shown in the diagram below.
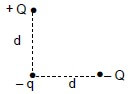
Which ONE of the following arrows CORRECTLY shows the direction of the net force acting on charge – q due to the presence of charges + Q and – Q? (2)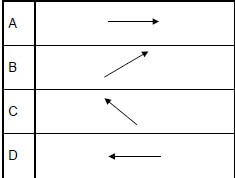
1.8 Learners investigate the relationship between current (I) and potential difference (V) at a constant temperature for three different resistors, X, Y and Z.
They obtain the graphs shown below. 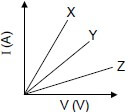
The resistances of X, Y and Z are RX, RY and RZ respectively.
Which ONE of the following conclusions regarding the resistances of the resistors is CORRECT?
- Rz > RY > Rx
- RX = RY = RZ
- RX > RY > RZ
- RX > RY and RY < RZ (2)
1.9 Which ONE of the following changes may lead to an increase in the emf of an AC generator without changing its frequency?
- Decrease the resistance of the coil.
- Increase the area of the coil.
- Increase the resistance of the coil.
- Decrease the speed of rotation. (2)
1.10 The wavelength of a monochromatic light source P is twice that of a monochromatic light source Q. The energy of a photon from source P will be … of a photon from source Q.
- a quarter of the energy
- half the energy
- equal to the energy
- twice the energy (2)
[20]
QUESTION 2 (Start on a new page.)
A learner constructs a push toy using two blocks with masses 1,5 kg and 3 kg respectively. The blocks are connected by a massless, inextensible cord.
The learner then applies a force of 25 N at an angle of 30o to the 1,5 kg block by means of a light rigid rod, causing the toy to move across a flat, rough, horizontal surface, as shown in the diagram below. 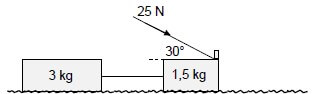
The coefficient of kinetic friction (µk) between the surface and each block is 0,15.
2.1 State Newton's Second Law of Motion in words. (2) 2.2 Calculate the magnitude of the kinetic frictional force acting on the 3 kg block. (3)
2.3 Draw a labelled free-body diagram showing ALL the forces acting on the 1,5 kg block. (5)
2.4 Calculate the magnitude of the:
2.4.1 Kinetic frictional force acting on the 1,5 kg block (3)
2.4.2 Tension in the cord connecting the two blocks (5)
[18]
QUESTION 3 (Start on a new page.)
A ball is dropped from the top of a building 20 m high. Ignore the effects of air resistance. 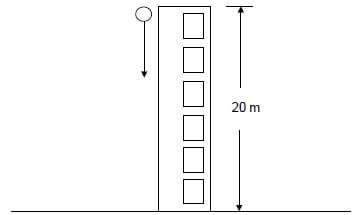
3.1 Define the term free fall. (2)
3.2 Calculate the:
3.2.1 Speed at which the ball hits the ground (4)
3.2.2 Time it takes the ball to reach the ground (3)
3.3 Sketch a velocity-time graph for the motion of the ball (no values required). (2)
[11]
QUESTION 4 (Start on a new page.)
The graph below shows how the momentum of car A changes with time just before and just after a head-on collision with car B.
Car A has a mass of 1 500 kg, while the mass of car B is 900 kg.
Car B was travelling at a constant velocity of 15 m∙s-1 west before the collision. Take east as positive and consider the system as isolated. 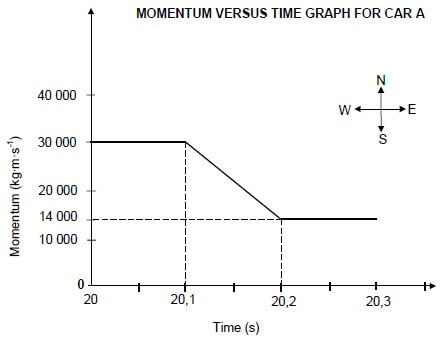
4.1 What do you understand by the term isolated system as used in physics? (1) Use the information in the graph to answer the following questions.
4.2 Calculate the:
4.2.1 Magnitude of the velocity of car A just before the collision (3)
4.2.2 Velocity of car B just after the collision (5)
4.2.3 Magnitude of the net average force acting on car A during the collision (4)
[13]
QUESTION 5 (Start on a new page.)
A pendulum with a bob of mass 5 kg is held stationary at a height h metres above the ground. When released, it collides with a block of mass 2 kg which is stationary at point A.
The bob swings past A and comes to rest momentarily at a position ¼ h above the ground.
The diagrams below are NOT drawn to scale. 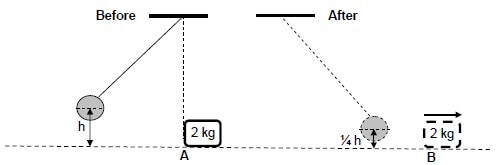
Immediately after the collision the 2 kg block begins to move from A to B at a constant speed of 4,95 m∙s-1.
Ignore frictional effects and assume that no loss of mechanical energy occurs during the collision.
5.1 Calculate the:
5.1.1 Kinetic energy of the block immediately after the collision (3)
5.1.2 Height h (4)
The block moves from point B at a velocity of 4,95 m·s-1 up a rough inclined plane to point C. The speed of the block at point C is 2 m·s-1. Point C is 0,5 m above the horizontal, as shown in the diagram below.
During its motion from B to C a uniform frictional force acts on the block. 
5.2 State the work-energy theorem in words. (2)
5.3 Use energy principles to calculate the work done by the frictional force when the 2 kg block moves from point B to point C. (4)
[13]
QUESTION 6 (Start on a new page.)
6.1 An ambulance is moving towards a stationary listener at a constant speed of 30 m∙s-1. The siren of the ambulance emits sound waves having a wavelength of 0,28 m. Take the speed of sound in air as 340 m∙s-1.
6.1.1 State the Doppler effect in words. (2)
6.1.2 Calculate the frequency of the sound waves emitted by the siren as heard by the ambulance driver. (3)
6.1.3 Calculate the frequency of the sound waves emitted by the siren as heard by the listener. (5)
6.1.4 How would the answer to QUESTION 6.1.3 change if the speed of the ambulance were LESS THAN 30 m∙s-1? Write down only
INCREASES, DECREASES or REMAINS THE SAME. (1)
6.2 An observation of the spectrum of a distant star shows that it is moving away from the Earth.
Explain, in terms of the frequencies of the spectral lines, how it is possible to conclude that the star is moving away from the Earth. (2)
[13]
QUESTION 7 (Start on a new page.)
7.1 In an experiment to verify the relationship between the electrostatic force, FE, and distance, r, between two identical, positively charged spheres, the graph below was obtained. 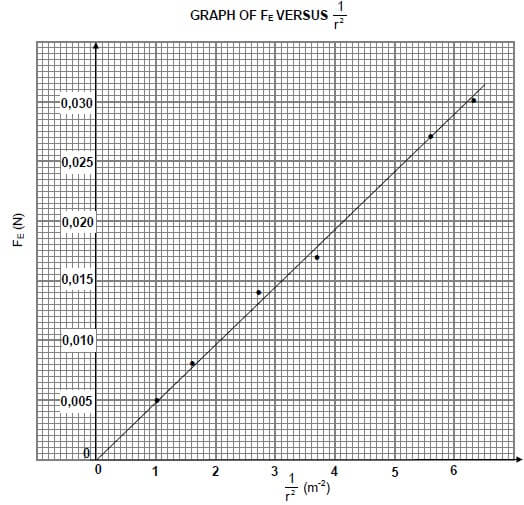
7.1.1 State Coulomb's law in words. (2)
7.1.2 Write down the dependent variable of the experiment. (1)
7.1.3 What relationship between the electrostatic force FE and the square of the distance, r2, between the charged spheres can be deduced from the graph? (1)
7.1.4 Use the information in the graph to calculate the charge on each sphere. (6)
7.2 A charged sphere, A, carries a charge of – 0,75 µC.
7.2.1 Draw a diagram showing the electric field lines surrounding sphere A. (2)
Sphere A is placed 12 cm away from another charged sphere, B, along a straight line in a vacuum, as shown below. Sphere B carries a charge of +0,8 μC. Point P is located 9 cm to the right of sphere A. 
7.2.2 Calculate the magnitude of the net electric field at point P. (5)
[17]
QUESTION 8 (Start on a new page.)
8.1 In the circuit below the battery has an emf (ε) of 12 V and an internal resistance of 0,2 Ω. The resistances of the connecting wires are negligible. 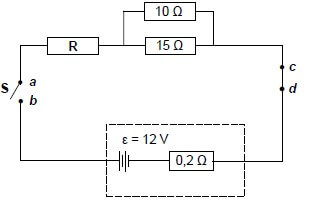
8.1.1 Define the term emf of a battery. (2)
8.1.2 Switch S is open. A high-resistance voltmeter is connected across points a and b. What will the reading on the voltmeter be? (1)
8.1.3 Switch S is now closed. The same voltmeter is now connected across points c and d. What will the reading on the voltmeter be? (1)
When switch S is closed, the potential difference across the terminals of the battery is 11,7 V.
Calculate the:
8.1.4 Current in the battery (3)
8.1.5 Effective resistance of the parallel branch (2) 8.1.6 Resistance of resistor R (4)
8.2 A battery with an emf of 12 V and an internal resistance of 0,2 Ω are connected in series to a very small electric motor and a resistor, T, of unknown resistance, as shown in the circuit below.
The motor is rated X watts, 3 volts, and operates at optimal conditions. 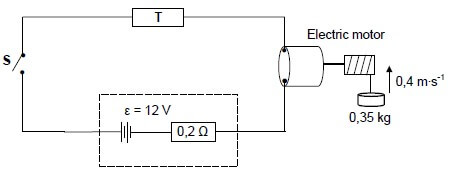
When switch S is closed, the motor lifts a 0,35 kg mass vertically upwards at a constant speed of 0,4 m∙s-1. Assume that there is no energy conversion into heat and sound.
Calculate the value of:
8.2.1 X (3)
8.2.2 The resistance of resistor T (5)
[21]
QUESTION 9 (Start on a new page.)
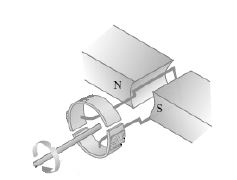
9.1 A generator is shown below. Assume that the coil is in a vertical position.
9.1.1 Is the generator above AC or DC? Give a reason for the answer. (2)
9.1.2 Sketch an induced emf versus time graph for ONE complete rotation of the coil. (The coil starts turning from the vertical position.) (2)
9.2 An AC generator is operating at a maximum emf of 340 V. It is connected across a toaster and a kettle, as shown in the diagram below. 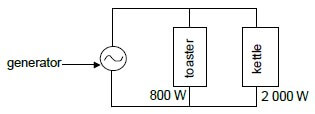
The toaster is rated at 800 W, while the kettle is rated at 2 000 W. Both are working under optimal conditions.
Calculate the:
9.2.1 rms current passing through the toaster (3)
9.2.2 Total rms current delivered by the generator (4)
[11]
QUESTION 10 (Start on a new page.)
10.1 A learner is investigating the photoelectric effect for two different metals, silver and sodium, using light of different frequencies. The maximum kinetic energy of the emitted photoelectrons is plotted against the frequency of the light for each of the metals, as shown in the graphs below. 
10.1.1 Define the term threshold frequency. (2)
10.1.2 Which metal, sodium or silver, has the larger work function? Explain the answer. (3)
10.1.3 Name the physical constant represented by the slopes of the graphs. (1)
10.1.4 If light of the same frequency is shone on each of the metals, in which metal will the ejected photoelectrons have a larger maximum kinetic energy? (1)
10.2 In a different photoelectric experiment blue light obtained from a light bulb is shone onto a metal plate and electrons are released. The wavelength of the blue light is 470 x 10-9 m and the bulb is rated at 60 mW. The bulb is only 5% efficient.
10.2.1 Calculate the number of photons that will be incident on the metal plate per second, assuming all the light from the bulb is incident on the metal plate. (5)
10.2.2 Without any further calculation, write down the number of electrons emitted per second from the metal. (1)
[13]
TOTAL: 150
DATA FOR PHYSICAL SCIENCES GRADE 12
PAPER 1 (PHYSICS)
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Acceleration due to gravity | g | 9,8 m•s-2 |
Universal gravitational constant | G | 6,67 × 10-11 N•m2•kg-2 |
Speed of light in a vacuum | c | 3,0 × 108 m•s-1 |
Planck's constant | h | 6,63 × 10-34 J•s |
Coulomb's constant | k | 9,0 × 109 N•m2•C-2 |
Charge on electron | e | -1,6 × 10-19 C |
Electron mass | me | 9,11 × 10-31 kg |
Mass of earth | M | 5,98 × 1024 kg |
Radius of earth | RE | 6,38 × 103 km |
TABLE 2: FORMULAE
MOTION
| vf = vi + aΔt | Δx = ViΔt + ½aΔt2 or Δy = ViΔt2 + ½aΔt2 |
Vf2 = Vi2 + 2aΔx or Vf2 = vi2 + 2aΔy | Δx = [Vi + Vf]Δt or Δy = [Vi + Vf]Δt |
FORCE
Fnet = ma | p= mv |
fsmax = µsN | fk = µkN |
FnetΔt = Δp | w =mg |
F = Gm1m2 | g = G M |
WORK, ENERGY AND POWER
W =FΔxcosθ | U= mgh or EP = mgh |
K = ½mv2 or Ek = ½mv2 | Wnet = ΔK or Wnet = ΔEk ΔK = Kf −Ki or ΔEk =Ekf − Eki |
Wnc= ΔK + ΔU or Wnc= ΔEk + ΔEp | P = W Δt |
Pav = Fv |
WAVES, SOUND AND LIGHT
v = f λ | T =1/f |
fl = v ± vl fs fl = v ± vl fb | E = hf or E = h c |
E = W0 + Ek where | |
ELECTROSTATICS
| F = kQ1Q2 r2 | E = KQ |
E = V | E = F |
V = W | n = Q |
ELECTRIC CIRCUITS
R = V | emf (ε) = I(R + r) |
RS = R1 + R2 + ....... | q = I Δt |
W = Vq | P= W |
ALTERNATING CURRENT
I rms = Imax | Paverage = VrmsIrms |