PHYSICAL SCIENCES PHYSICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2016

Tuesday, 15 June 2021 09:15

PHYSICAL SCIENCES PHYSICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2016

More in this category: « LIFE SCIENCES PAPER 2 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2016 COMPUTER APPLICATIONS TECHNOLOGY PAPER 2 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2016 »

Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

PHYSICAL SCIENCES
PHYSICS PAPER 1
GRADE 12
NSC EXAM PAPERS AND MEMOS
NOVEMBER 2016

MEMORANDUM

1.1 A ✓✓ (2)
1.2 C ✓✓ (2)
1.3 C ✓✓ (2)
1.4 D ✓✓ (2)
1.5 B ✓✓ (2)
1.6 A ✓✓ (2)
1.7 C ✓✓ (2)
1.8 A ✓✓ (2)
1.9 B ✓✓ (2)
1.10 B ✓✓ (2) [20]

QUESTION 2
2.1 When a resultant/net force acts on an object, the object will accelerate in the (direction of the net/resultant force). The acceleration is directly proportional to the net force ✔and inversely proportional to the mass ✔of the object.
OR
The resultant/net force acting on the object is equal (is directly proportional to) to the rate of change of momentum of an object (in the direction of the force). ✔✔ (2)

2.2 (3)

f_k = μ_kN✔= μ_kmg
= (0,15)(3)(9,8)✔
= 4,41 N✔

2.3

Accepted Labels
w	Fg/Fw/force of Earth on block/weight/14,7 N/mg/gravitational force
N	FN/Fnormal/normal force
T	Tension/FT
f_k	f_{kinetic friction}/f_f/w/f//F_f/wkinetic frictiong
25 N	Fapplied/FA/F

2.4.1 (3)

OPTION 1

f_k = μ_kN = μ_k(25sin 30º + mg)
= 0,15[(25sin30º)✔ + (1,5)(9,8)✔]
= 4,08 N✔

OPTION 2

f_k = μ_kN = μ_k(25cos 60º + mg)
= 0,15[(25cos60º)✔ + (1,5)(9,8)✔]
= 4,08 N✔

2.4.2

POSITIVE MARKING FROM QUESTION 2.2 AND QUESTION 2.4.1
OPTION 1
For the 1,5 kg block
F_net = ma ✔
F_x + (-T) +(- f_k) = ma
25 cos 30º – T – f_k = 1,5a
(25 cos 30º – T) – 4,08 ✔= 1,5a
17,571 – T = 1,5a ……….(1) ✔
either AS ABOVE OR BELOW
For the 3 kg block
T – f_k = 3a
T – 4,41✔ = 3a ………….(2)
13,161 = 4,5 a
a = 2,925 m∙s-²
T = 13,19 N ✔ (13,17 N – 13,19 N)

OPTION 2
For the 1,5 kg block
F_net = ma ✔
Fx + (-T) +(- f_k) = ma
25 cos 30º – T – f_k = 1,5a
(25 cos 30o – T) – 4,08 ✔= 1,5a
17,571 – T = 1,5a ……….(1)✔
either one
For the 3 kg block
T – f_k = 3a
T – 4,41✔ = 3a ………….(2)
35,142 – 2T = T – 4,41
T = 13,18 N ✔

OPTION 3
For the 1,5 kg block
F_net = ma ✔
F_x + (-T) +(- f_k) = ma
25 cos 30º – T – f_k = 1,5a
(25 cos 30º – T) – 4,08 ✔
= 1,5a 17,571 – T = 1,5a ……….(1) ✔
either one
a = 17,571− T
1,5
For the 3 kg block
T – f_k = 3a
T – 4,41✔ = 3a ………….(2)
a = T − 4,41
3
17,571− T = T − 4,41
1,5 3
T = 13,18 N✔

(5)
[18]

QUESTION 3
3.1 The motion of an object under the influence of gravity/weight/gravitational force only / Motion in which the only force acting is the gravitational force.✔✔ (2)

OPTION 1
Upwards positive:
vf² = vi² + 2aΔy ✔
= 02⁺ (2)(-9,8)✔(-20)✔
vf = 19,80 m∙s^-1 ✔
Downwards positive
vf² = vi² + 2aΔy ✔
= 02 + (2)(9,8)✔(20)✔
vf = 19,80 m∙s^-1✔

OPTION 2
Upwards positive:
Δy = viΔt + ½ aΔt²-20 = 0 + ½ (-9,8) Δt²✔
✔either one
Δt = 2,02 s
vf = vi + aΔt
= 0 + (-9,8)(2,02) ✔
= -19,80 m∙s^-1
= 19,80 m∙s^-1✔
Downwards positive
Δy = viΔt + ½ aΔt²20 = 0 + ½ (9,8) Δt²✔
✔either one
Δt = 2,02 s
vf = vi + aΔt
= 0 + (9,8)(2,02)✔
= 19,80 m∙s^-1✔

OPTION 3
(E_mech)_Top = (E_mech)_Ground✔1 mark for any
(E_P +E_K)_Top = (E_P +E_K)_Bottom(mgh + ½ mv²)_Top = (mgh + ½ mv²)_Bottom(9,8)(20) + 0✔ = (0 + ½vf²)✔
vf = 19,80 m∙s^-1✔

OPTION 4
W_nc = ΔE_p + ΔE_k ✔
0 = mgΔh + ½ mΔv²
0✔ = m(9,8)(0 – 20) + ½ m(v_f² – 0) ✔
vf = 19,80 m∙s^-1✔

OPTION 5
W_net = ΔE_k ✔
mgΔxcos0º = ½ m(v_f² – 0)
m(9,8)(20)(1)✔ = ½ mv_f² ✔
vf = 19,80 m∙s^-1✔

(4)

3.2.2

POSITIVE MARKING FROM QUESTION 3.2.1
OPTION 1
Downwards positive
v_f = v_i + aΔt ✔
19,80 = 0 + (9,8)Δt ✔
Δt = 2,02 s ✔

Upwards positive
v_f = v_i + aΔt ✔
-19,80 = 0 + (-9,8)Δt ✔
Δt = 2,02 s ✔

OPTION 2
Upwards positive:
Δy = v_iΔt + ½ aΔt²✔
-20 = 0 + ½ (-9,8) Δt²✔
Δt = 2,02 s✔

Downwards Positive
Δy = v_iΔt + ½ aΔt²✔
20 = 0 + ½ (9,8) Δt²✔
Δt = 2,02 s✔

OPTION 3
Downwards positive:
Δy = [ v₁ + v_f] Δt
2
20 = [ 0 + 19,80] Δt
2
Δt = 2,02 s✔

Upwards positive:

Δy = [ v₁ + v_f] Δt
2
-20 = [ 0 - 19,80] Δt
2
Δt = 2,02 s✔

(3)

3.3

Downward positive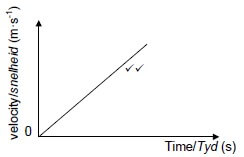

Upward positive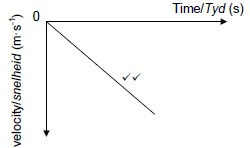

Notes

✔✔	Straight line through the origin.

(2)
[11]

QUESTION 4
4.1 A system on which the resultant/net external force is zero✔ A system which excludes external forces (1)
4.2.1 (3)

OPTION 1
p = mv✔
30 000 = (1 500)v ✔
v = 20 m∙s^-1✔

OPTION 2
Δp = mv_f – mv_i ✔
0 = (1 500)v_f – 30 000 ✔
v = 20 m∙s^-1✔

4.2.2 POSITIVE MARKING FROM QUESTION 4.2.1

OPTION 1

∑pi = ∑pf
m₁ v_1i + m₂v_2i = m₁ v_1f + m₂v_2f✔ 1 mark for any30 000 + (900)(-15)✔ = 14 000 + 900vB✔
∴vB = 2,78 m∙s-1 ✔east ✔ (Accept: to the right)

OPTION 2
ΔpA = -ΔpB
1 mark for any
p_f – p_i = -(mv_f - mv_i)
14 000 – 30 000 ✔= 900v_f – 900(-15) ✔
v_f = 2,78 m∙s^-1✔ east✔ (Accept: to the right)

(5)

4.2.3

OPTION 1

Slope = Δp = F_net✔
Δt
= (14 000 − 30 000) ✔
(20,2 - 20,1) ✔
= - 160 000
F_net = 160 000 N ✔

OPTION 2
F_netΔt = Δp ✔
F_net(0,1)✔ = 14 000 – 30 000✔
F_net = - 160 000 N
F_net = 160 000 N ✔

POSITIVE MARKING FROM QUESTION 4.2.2
OPTION 3
F_netΔt = Δp ✔
F_net(0,1)✔ = 900[(2,78) – (-15)]✔
F_net = 160 020 N
F_A = - F_BF_net = 160 020 N ✔

OPTION 4 p = mv 14 000 = 1 500v_f ✔ v_f = 9,33 m∙s^-1
F_net = m(vf - vi) ✔ 1500(9,33 − 20)✔ ∆t 0,1 = -160 050 = 160 050 N ✔	v_f = v_i + aΔt 9,33 = 20 + a(0,1) a = -106.7 m∙s^-2 F_net = ma ✔ = 1 500(-106,7) ✔ F_net = - 160 050 N F_net = 160 050 N ✔

(4)
[13]

QUESTION 5
5.1.1 E_k/K = ½ mv² ✔
= ½ (2)(4,95)² ✔
= 24,50 J ✔ (3)

5.1.2 (4)

POSITIVE MARKING FROM QUESTION 5.1.1 OPTION 1 E_{mech before} = E_{mech after}[(E_mech)_bob + (E_mech)_block ]_before = [(E_mech ) _Block + (E_mech)_bob_]after (mgh + ½ mv²)b_efore = (mgh + ½ mv²)_afterAny one ✔ (5)(9,8)h + 0 + 0 ✔= 5(9,8)¼h + 0 + 24,50 ✔ h = 0,67 m✔
OPTION 2 W_nc = ΔE_p + ΔE_k0 = ΔE_p + ΔE_k Any one ✔ -ΔE_p = ΔE_k -[(5)(9,8)(¼h) – (5)(9,8)h]✔ = 24,50✔ h = 0,67 m ✔	OPTION 3 Loss Ep bob = Gain in Ek of block ✔ mg(¾h) = 24,5 (5)(9,8)(¾h)✔ = 24,5 ✔ h = 0,67 m ✔
OPTION 4 Before (mgh + ½ mv²)_top = (mgh + ½ mv²)_bottom(5)(9,8)h + 0 = (5)(9,8)h_o + ½ (5)v²vi² = 19,6h - 19,6h_o After (mgh + ½ mv²)_bottom = (mgh + ½ mv²)_top(5)(9,8)h_o + ½(5)vf² = (5)(9,8)(¼h) + 0 vf² = 4,9h – 19,6h_o E_mech before collision = E_mech after collision✔ ½ mvi²(bob) + 0 = ½ mvf²(bob)+ ½ mv²(block) ½ (5)(19,6h – 19,6h_o) ✔ = ½ (5)(4,9h -19,6h_o) + 24,5 ✔ h = 0,67 m✔

5.2 The net/total work done on an object is equal ✔to the change in the object's kinetic energy ✔
OR
The work done on an object by a resultant/net force is equal to the change in the object's kinetic energy. (2)

5.3

OPTION 1
W_net = ΔEK✔
W_f + mgΔycosθ = ½m(v_f² - v_i² )
W_f +(2)(9,8)(0,5)cos180^o ✔ = ½ (2)(2² – 4,95²) ✔
W_f = - 10,7 J✔

OPTION 2
W_nc = ΔE_K + ΔU ✔
W_nc = ΔE_K + ΔE_P
W_f = ½ (2)(2² – 4,95²) ✔ + (2)(9,8)(0,5-0) ✔
= - 10,7 J✔

(4)
[13]

QUESTION 6
6.1

6.1.1 It is the (apparent) change in frequency (or pitch) of the sound (detected by a listener) ✔ because the sound source and the listener have different velocities relative to the medium of sound propagation. ✔
OR
An (apparent) change in (observed/detected) frequency (pitch), (wavelength) ✓as a result of the relative motion between a source and an observer ✓(listener). (2)

6.1.2

v = fλ ✔
340 = f(0,28) ✔
f_s = 1 214,29 Hz ✔ (3)

6.1.3 POSITIVE MARKING FROM QUESTION 6.1.2

f_L = v ± v_Lf_s OR f_L = v ± v_L × v OR f_L = v f_s OR F_L = f_s
  v ± v_s v ± v_s λ_s v - v_s 1 - ^v_s/_v
f_L =   340   1214,29 OR f_L =   340    ×     340    OR F_L = 1214,29
(340 - 30) (340 - 30) 0,28    1 - ³⁰/₃₄₀
= 1 331,80 Hz✔ (1 331,80 Hz – 1 335,72 Hz) (5)
6.1.4 Decreases ✔ (1)

6.2 The spectral lines of the star are/should be shifted towards the lower frequency ✔ end, which is the red end (red shift) of the spectrum. ✔

(2)
[13]

QUESTION 7

7.1.1 The (magnitude of the) electrostatic force exerted by one (point) charge on another is directly proportional to the product of the charges ✓ and inversely proportional to the square of the distance between their (centres) them. ✓ (2)
7.1.2 FE/Electrostatic force✓ (1)
7.1.3 The electrostatic force is inversely proportional to the square of the distance between the charges ✔
OR
The electrostatic force is directly proportional to the inverse of the square of the distance between the charged spheres (charges). ✔
OR
F α 1 ✔
r²OR
They are inversely proportional to each other (1)

7.1.4 (6)

OPTION 1
1 mark for using slope
Slope = ∆F_E ✔ = (O,027 - 0)
∆¹/_r² ✔ (5,6 - 0)
= 4,82 x 10^-3 N∙m² (4,76 x 10^-3 – 5 x 10^-3)
Slope = F_Er² = kQ₁Q₂ = kQ₂ ✔
4,82 x 10^-3 ✓= 9 x 10⁹ Q² ✓
∴ Q = 7,32 x 10^-7C ✔
OPTION 2
Accept any pair of points on the line
F = kQ₁Q₂✔
r²( ) ✔ = (9 × 10⁹) Q² ✔
( ) ✔✔
Q = 7,32 x 10^-7C ✔
(7,32 x 10^-7 – 7,45 x 10^-7 C)

Examples

( 0,005) ✔ = (9 × 10⁹) Q² ✔
( 1 ) ✔✔
Q = 7,45 x 10^-7 C ✔

(0,027 ) ✔ = (9 × 10⁹) Q² ✔
(¹/_5,6) ✔✔

Q = 7,32 x 10^-7 C ✔

7.2.1

Criteria for drawing electric field:	Marks
Direction	✓
Field lines radially inward	✓

7.2.2
E = kQ
r²
Take right as positive
E_PA = (9 × 10⁹) (0,75 ×10^-6) ✔
(0,09)²
= 8,33 x 10⁵ N∙C^-1 to the left
E_PB = (9 × 10⁹) (0,8 ×10^-6) ✔
(0,03)²= 8 x 10⁶ N∙C^-1 to the left
E_net = E_PA + E_PC
= [-8,33 x 10⁵ + (- 8 x 10⁶)] ✔
= -8,83 x 10⁶
= 8,83 x 10⁶ N∙C^-1✔
1 mark for the addition of same signs
Take left as positive
E_PA = (9 × 10⁹) (0,75 ×10^-6) ✔
(0,09)²= 8,33 x 10⁵ N∙C^-1 to the left
EPB = (9 × 10⁹) (0,8 ×10^-6) ✔
(0,03)²
= 8 x 10⁶ N∙C^-1 to the left
E_net = E_PA + E_PC = (8,33 x 10⁵ + 8 x 10⁶) ✔
1 mark for the addition of same signs
= 8,83 x 10⁶ N∙C^-1 ✔

(5)
[17]

QUESTION 8
8.1.1 (Maximum) energy provided (work done) by a battery per coulomb/unit charge passing through it ✔✔ (2)
8.1.2 12 (V)✔ (1)
8.1.3 0 (V) / Zero✔ (1)
8.1.4

ε = I(R + r)
ε = V_ext + V_int12 = 11,7 +Ir
0,3 = I_tot(0,2) ✔
I_tot = 1,5 A ✔

OR
V = IR ✔ (Accept: V_”lost” = Ir)
0,3 = I_tot(0,2) ✔
I_tot = 1,5 A✔ (3)

OPTION 1
1 = 1 + 1
R_// R₁ R_{2
1 = 1 + 1
R_// 10 15}R = 6 Ω ✔

OPTION 2

R_|| = R₁R₂
R₁ + R₂
R_|| = (10)(15)
10 + 15
= 6 Ω ✔

(2)

POSITIVE MARKING FROM QUESTIONS 8.1.4 AND 8.1.5
OPTION 1
V = IR ✔
11,7✔ = 1,5(6 + R) ✔
R = 1,8 Ω ✔
OR
V = IR ✔
11,7 = 1,5R ✔
R = 7,8 Ω
R_R = 7,8 – 6 ✔
= 1,8 Ω ✔

OPTION 2
ε = I(R + r) ✔
12 = 1,5(R + 0,2) ✔
R = 7,8 Ω
RR = 7,8 – 6 ✔
= 1,8 Ω ✔

OPTION 3
V_||= IR_||
= (6)(1,5) ✔
= 9 V
V_R = IR ✔
(11,7 - 9) = (1,5)R✔
R = 1,8 Ω✔

(4)

8.2.1 (3)

P_ave= Fv_ave✔= mg(v_ave)
= (0,35)(9,8)(0,4)✔
= 1,37 W✔
OR
P = W_nc = ∆E_k + ∆E_p =0 + (0,35)(9,8)(0,4 − 0)✔= 1,37 W ✔
∆t ∆t 1
OR
P = W= E = (0,35)(9,8)(0,4 )✔= 1,37 W ✔
∆t ∆t 1

8.2.2

POSITIVE MARKING FROM QUESTION 8.2.1
OPTION 1 P = VI 1,37 = (3)I ✔ I = 0,46 A ✔Any one ε = V_ext + V_int = V_T + V_X + V_int12 = V_T + 3 + (0,2)(0,46) ✔ V_T = 8,91 V V_T = IR_T8,91 = (0,46)R_T ✔ RT = 19,37 Ω✔	OPTION 2 P = V² R 1,37 = 3²✔ R R = 6,57 Ω ✔Any one P = VI 1,37 = (3)I ✔ I = 0,46 A ε = I(R + r) 12 = 0,46(6,57 + R_T + 0,2) ✔ R_T = 19,38 Ω ✔

OPTION 3
P = VI ✔
1,37 = (3)I ✔
I = 0,46 A

P_tot = P_r + P_motor + P_T(12)(0,46)✔ = (0,46)²(0,2) + 1,37 + (0,46)²R_T ✔
R_T = 19,41 Ω ✔
OR
P = VI ✔
1,37 = (3)I ✔
I = 0,46 A
P_tot = P_r + P_motor + P_T(12)(0,46) = (0,46)²(0,2) + 1,37 + PT ✔
P_T = 4,07 W
P=I²R
4,07 = (0,46)2R_T ✔
R_T = 19,49 Ω ✔

OPTION 4
P = VI
1,37 = (3)I ✔
I = 0,46 A

✔Any one

ε = I(R + r)
12 = (0,46)(R + 0,2) ✔
R = 25,87 Ω

V = IR
3 = (0,46)R✔
R = 6,52 Ω
RT = 25,87 – 6,52
= 19,35 Ω ✔

P = I²R
1,37 = (0,46)²R✔
R = 6,47 Ω
RT = 25,87 – 6,47
= 19,4 Ω ✔

P_motor = V²
R
1,37 = 3²
R
R = 6,56 Ω
RT = 25,87 – 6,56

= 19,31 Ω ✔

(5)
[21]

QUESTION 9
9.1.1 DC/GS-generator✔
Uses split ring/commutator✔ (2)
9.1.2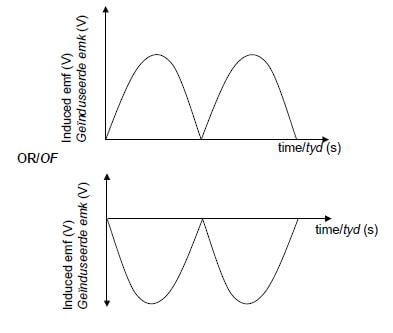

9.2.1

OPTION 1
V_rms = V_max
√2
P_ave = V_rmsI_rms ✓
800 = 340 (I_rms )
√2
I_rms = 3,33 A ✓

OR
V_rms = V_max
√2
= 340 = 240,416
√2
P_ave = V_rmsI_rms ✓
800 = I_rms (240,416)
I_rms = 3,33 A ✓

9.2.2

OPTION 2
P_ave =( V²_rms) = ✓ ( V²_rms)
R (2)(R)
800 = 340² (I_rms )
(√2)²(R)
R = 72,25 Ω

EITHER:
P_ave = I_rms²R
800 = I_rms²(72,25)
I_rms² = 3,33A
OR:
V_rms = I_rmsR
I_rms = 240,416 ✓
72, 25
= 3,33 A✓

(3)

POSITIVE MARKING FROM QUESTION 9.2.1
OPTION 1
P_ave = V_rmsI_rms= I ✓
for the kettle:
2000 = 340 (I_rms) rms✓
√2
I_rms = 8,32 A
I_tot = (8,32 + 3,33) ✓
= 11,65 A ✓

OPTION 2
P_ave = (V²_rms) = (V²_max) ✓
R (2)(R)
800 = 340²
(√2)²(R)
R = 72,25 Ω

2000 =   340²
(√2)²(R₂₀₀₀)
R =  28,9 Ω
1 = 1 + 1 ⇒ ⇒ ⇒  ⇒ R = (28,9)(72,25) = 20,64 Ω
R    R₁ R₂ (28,9 + 72,25)
V_rms = I_rmsR
240,42 = I_rms20,64) ✓
I_rms= 11,65 A✓

OPTION 3
P_ave = V_rms I_rms ✓ = V_maxI_max
2
2800 = (380) I_rms✓
2
I_max = 16,47 A
I_rms ✓ = I_max₌16,47
√2 √2
I_rms = 11,65 A✓

OPTION 4
Pa_ve = V_rmsI_rms✓
2 800 ✔= 340 I_rms✔
√2
I_rms = 11,65 A ✔

OPTION 5
P_T : P_K800 : 2 000 ✔
1 : 2,5

I_T : I_K3,33 : 8,325 ✔
I_rms = 3,33 + 8,325 ✔
= 11,66 A ✔

(4)
[11]

QUESTION 10
10.1

10.1.1 The minimum frequency (of a photon/light) needed✓ to emit electrons from (the surface of) a metal. (substance) ✓
OR
The frequency (of a photon/light) needed✓ to emit electrons from (the surface of) a metal. (substance) with zero kinetic energy✓ (2)
10.1.2 Silver/Silwer✔
Threshold/cutoff frequency (of Ag) is higher✔
W_o α f_o / W_o = hf_o ✔
OR
To eject electrons with the same kinetic energy from each metal, light of a higher frequency/energy is required for silver. ✓ Since E = W_o + E_k(_max) (and E_k is constant), the higher the frequency/energy of the photon/light required, the greater is the work function/W_o.✓ (3)
10.1.3 Planck’s constant ✔ (1)
10.1.4 Sodium✔ (1)

10.2

10.2.1 Energy radiated per second by the blue light

= (⁵/₁₀₀)(60 x 10^-3) ✔ = 3 x 10^-3 J∙s^-1E_photon = hc ✔
λ
= (6,63 × 10^-34 )(3 × 10⁸)
470 × 10^-9 = 4,232 x 10^-19J ✔
Total number of photons incident per second
= 3 × 10^-3
4,232 × 10¹⁵
= 7,09 x 10¹⁵ ✔ (5)
10.2.2 POSITIVE MARKING FROM QUESTION 10.2.1
7,09 x 10¹⁵ (electrons per second) ✔
OR
Same number as that calculated in Question 10.2.1 above (1)

[13]
TOTAL: 150

Last modified on Wednesday, 16 June 2021 08:11

Published in Grade 12 NSC Exam Papers and Memos 2016 November

PHYSICAL SCIENCES PHYSICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2016

MEMORANDUM

Related items