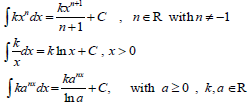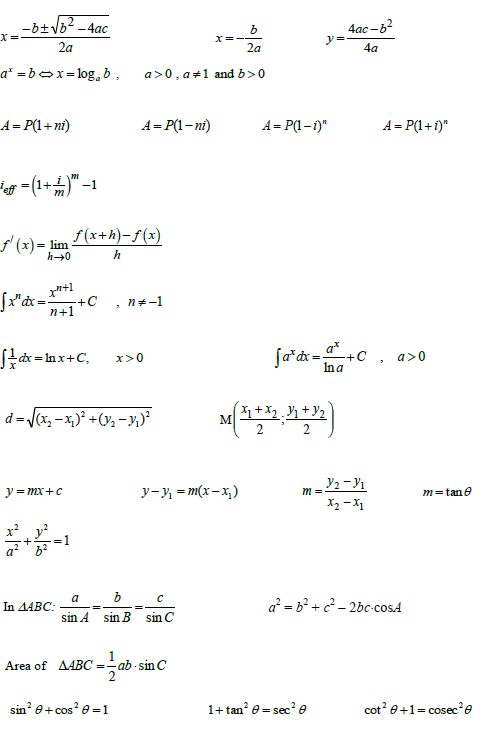TECHNICAL MATHEMATICS GRADE 12 - EXAMINATION GUIDELINES 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupTECHNICAL MATHEMATICS
EXAMINATION GUIDELINES
GRADE 12
2021
TABLE OF CONTENTS
| Page | |
| 1. INTRODUCTION | 3 |
| 2. ASSESSMENT IN GRADE 12 4 2.1 Format of question papers for Grade 12 4 2.2 Weighting of cognitive levels 5 | 4 4 5 |
| 3. ELABORATION OF CONTENT FOR GRADE 12 (CAPS) | 6 |
| 4. ACCEPTABLE REASONS: EUCLIDEAN GEOMETRY | 11 |
| 5. INFORMATION SHEET | 14 |
| 6. GUIDELINES FOR MARKING | 16 |
| 7. CONCLUSION | 16 |
- INTRODUCTION
The Curriculum and Assessment Policy Statement (CAPS) for Technical Mathematics outlines the nature and purpose of the subject. This guides the philosophy underlying the teaching and assessment of the subject in Grade 12.
The aim of Technical Mathematics is to apply the science of Mathematics to the technical field where the emphasis is on APPLICATION and not on abstract ideas.
Specific aims are:
Mathematical modelling is an important focal point of the curriculum and those real-life technical problems should be incorporated into all sections whenever appropriate.
The purpose of these examination guidelines is to:- Provide clarity on the depth and scope of the content to be assessed in the Grade 12 National Senior Certificate (NSC) Examination in Technical Mathematics;
- Assist teachers to prepare learners adequately for the examinations.
This document deals with the final Grade 12 external examinations. It does not deal in any depth with the school-based assessment (SBA), performance assessment tasks (PATs) or final external practical examinations as these are clarified in a separate PAT document which is updated annually.
These examination guidelines should be read in conjunction with the following documents: - The National Curriculum Statement (NCS) Curriculum and Assessment Policy Statement (CAPS): Technical Mathematics
- The National Protocol of Assessment: An addendum to the policy document, the National Senior Certificate: A qualification at Level 4 on the National Qualifications Framework (NQF), regarding the National Protocol for Assessment (Grades R–12)
- The national policy pertaining to the programme and promotion requirements of the National Curriculum Statement, Grades R–12
- ASSESSMENT IN GRADE 12
All candidates will write TWO external papers, as prescribed.
2.1 Format of Question Papers for Grade 12
Questions in Papers 1 and 2 will assess performance at different cognitive levels with the emphasis on process skills, critical thinking, scientific reasoning and strategies to investigate and solve problems in a variety of contexts. INTEGRATION OF CONTENT AREAS IS POSSIBLE.PAPER TOPICS Weighting of content areas DURATION TOTAL DATE MARKING 1 Number Systems (binary and complex numbers)
Algebra (expressions, equations and inequalities including nature of roots, exponents, surds and logarithms)
50 ± 3 3 hours 150 November External Functions and graphs 35 ± 3 Finance, growth and decay 15 ± 3 Differential calculus and integration 50 ± 3 2 Analytical Geometry 25 ± 3 3 hours 150 November External Euclidean Geometry 40 ± 3 Trigonometry 50 ± 3 Mensuration, circles, angles and angular movement 35 ± 3
NOTE: An information sheet is included in this document.
2.2 Weighting of Cognitive Levels
Papers 1 and 2 will include questions in four cognitive levels. The distribution of cognitive levels in the papers is given below.
NOTE: The weighting has been modified relative to the CAPS document.COGNITIVE LEVEL DESCRIPTION OF SKILLS TO BE DEMONSTRATED WEIGHTING (plus, minus) APPROXIMATE NUMBER OF MARKS IN A 150-MARK PAPER Knowledge Recall
Identification of correct formula on the information sheet (no changing of the subject)
Use of mathematical facts
Appropriate use of mathematical vocabulary
Algorithms
Estimation and appropriate rounding of numbers
Definitions
Properties of functions
(25 ± 2 )% 34 to 40 marks Routine procedures Perform well-known procedures
Simple applications and calculations which might involve few steps
Derivation from given information may be involved
Identification and use (after changing the subject) of correct formula
Generally similar to those encountered in class
(45 ± 2 )% 64 to 70 marks Complex procedures Problems involve complex calculations and/or higher-order reasoning
There is often not an obvious route to the solution
Problems need not be based on a real-life context
Could involve making significant connections between different representations
Require conceptual understanding
Learners are expected to solve problems by integrating different topics
(20 ± 2 )% 27 to 33 marks Problem solving Non-routine problems (which are not necessarily difficult)
Problems are mainly unfamiliar
Higher order reasoning and processes are involved
Might require the ability to break the problem down into its constituent parts
Interpreting and extrapolating from solutions obtained by solving problems based in unfamiliar contexts.
(10 ± 2 )% 12 to 18 marks
- ELABORATION OF CONTENT/TOPICS FOR GRADE 12 (CAPS)
The purpose of the clarification of the topics is to give guidance to the teacher in terms of depth of content necessary for examination purposes. The integration of topics is encouraged as learners should understand and apply the science of Mathematics to the technical field where the emphasis is on application and not on abstract ideas.
3.1 Number System
Candidates must be able to:- Determine between which two integers a given simple surd lies
- Perform four basic operations using binary numbers
- Convert whole numbers to binary numbers and vice versa
- Set builder notation, interval notation and number line
- Add, subtract, divide and multiply complex numbers
- Represent complex numbers in the Argand diagram
- Determine the modulus (r) and the argument (θ) of a complex number z
- Express a complex number in a trigonometric or a polar form
- Solve equations with complex numbers with two variables
3.2 Functions and Graphs
Candidates must be able to: - Work with relationships between variables in terms of numerical, graphical, verbal and symbolic representations of functions and convert flexibly between these representations (tables, graphs, words and formulae)
- Determine the effects of the parameter which results in a vertical/horizontal shift and that which results in a vertical/horizontal stretch and/or reflection about the x-axis and y-axis
- Deduce the equations if critical points are given
- Sketch graphs using tables, calculate critical points to sketch graphs and identifying domain, range, axes of symmetry and asymptotes for prescribed functions
Linear: y mx c
y - y1 = m(x-x1)
Quadratic : y = f(x)=a(x+p)2+q
y = ƒ(x)=a(x2+ bx + c
Hyperbola : y =a + q ;
x
Exponential : y = aƒ(x)=abx + q where a≠ 0; b > 0 and b ≠ 1 - Draw and work with graphs:
Circle: x2 + y2 = r2
Semi-circle : y = + √r2-x2
y = √r2-x2 - Draw graphs of the functions defined by:
y = a sinx y=a cosx
y = a sinx + q; y=a cosx + q
y = sin (ax); y= cos(ax)
y = sin (x + p); y=cos(x + p)
y = a tanx
for 0º ≤ x ≤ 360º
NOTE: Trigonometric functions will be assessed in Paper 2.
3.3 Finance, Growth and Decay
Candidates must be able to: - Understand implications of fluctuating foreign exchange rates
- Use simple and compound growth formulae A = P (1 + in) and A = P(1 + i)n
- Use simple and compound decay formulae A = P (1 – in) and A = P(1 – i )n to solve problems (including interest, hire purchase, inflation, population growth and other real life problems)
- Analyse the effect of different periods of compounding growth and decay (including effective and nominal interest rates), not limited to finance
- Critically analyse different loan options
NOTE: Applications must be real and NOT contrived.
3.4 Algebra
Candidates must be able to: - Apply the laws of exponents to expressions and equations involving rational exponents
- Add, subtract, multiply and divide simple surds
- Demonstrate an understanding of the definition of a logarithm and any laws needed to solve real-life problems and NOT CONTRIVED problems
- Apply laws of logarithm to solve real-life problems
- Apply remainder and factor theorems for polynomials up to the third degree
- Factorise third-degree polynomials (including examples which require the factor theorem)
- Solve quadratic equations (by factorisation and by using the quadratic formula)
- Solve equations in two unknowns, one of which is linear and the other quadratic, algebraically or graphically
- Solve word problems leading to simultaneous equations, one of which is linear and the other quadratic
- Determine the nature of roots and the conditions for which the roots are real, non-real, equal, unequal, rational and irrational
3.5 Differential Calculus and Integration
Candidates must be able to: - Determine the average gradient of a curve between two points
- Determine the gradient of a tangent to a graph, which is also the gradient of the graph at that point
- Differentiate, from first principles, functions defined by:
ƒ(x) = k ; ƒ (x) = ax and ƒ (x) = ax + b - Use the rule of differentiation d (axn) = axn-1 for n∈R
dx - Determine the equations of tangents to graphs of functions
- Sketch graphs of cubic polynomial functions using differentiation to determine the coordinates of stationary points. Also determine the x-intercepts using the factor theorem and other techniques.
- Analyse the information from graphs, make deductions, read value(s) or intervals from graphs
- Solve practical problems involving optimisation and rates of change including the calculus of motion and be able to interpret solutions and make conclusions.
- Integrate the following forms of integrals:
- Integrate polynomials consisting of terms of the above forms
- Apply integration to determine the magnitude of an area included by a curve and the x-axis or by a curve, the x-axis and the ordinates x = a and x = b where a, b∈Z. The sketch must be provided.
3.6 Euclidean Geometry
Candidates must be able to: - State properties of special triangles (scalene, isosceles, equilateral and right-angled triangle) and quadrilaterals
- Define various polygons (including the scalene, isosceles, equilateral and right-angled triangle, the kite, parallelogram, rectangle, rhombus, square and trapezium)
- Apply circle theorems and their converses in calculations to solve geometry problems providing reasons for statements when required
- Apply the concept of similarity and proportionality
- Apply proportionality in triangles
- Apply mid-point theorem
NOTE: Proofs of theorems and their converses will not be examined.
3.7 Mensuration
Candidates must be able to: - Convert units, square units and cubic units
- Solve problems involving volume and surface area of solids studied in earlier grades and combinations of those objects to form more complex shaped solids
- Determine the area of an irregular figure using mid-ordinate rule
NOTE: The questions based on the surface area and volume of right prisms, pyramids, cones and spheres, should be provided to learners with relevant formulae whereby they are expected to select the correct formula to use.
3.8 Circles, Angles and Angular Movement
Candidates must be able to: - Define radian
- Convert degrees to radians and vice versa
- Use relationship between central angles and arcs
- Calculate area of a sector: r=radius, s=arc length and θ= central angle in radians
- Calculate height of segments: 4h2 4dh x2 0 , h = height of segment, d = diameter of circle, x = length of chord
- Calculate the area of a segment
- Calculate angular velocity (Omega): 2 n 360 n , n = rotation frequency
- Calculate circumferential velocity: Dn , D = diameter and n = rotation frequency
3.9 Analytical Geometry - Candidates must be able to:
- Calculate the distance between the two points
- Calculate the gradient of the line segment joining the points
- Calculate the co-ordinates of the mid-point of the line segment joining the points
- Determine the equation of a straight line joining the two points
Determine the equation of a line through two given points - Determine the equation of a line through one point and parallel or perpendicular to a given line
- Determine the angle of inclination of a line
- Determine the equation of a circle with centre at the origin (centre is (0;0));
- Determine the equation of a tangent to a circle at a given point on the circle
- Determine point(s) of intersection of a circle and a straight line
- Plot the graph of an ellipse: x2 + y 2 = 1
a2 a2
NOTE: Include REAL-LIFE APPLICATIONS.
3.10 Trigonometry
Candidates must be able to: - Know the basic trigonometric ratios and take note that there are special names for the reciprocals of the trigonometric functions
- Refer to special angles (calculating without using a calculator)
- Simplify trigonometric expressions/equations by making use of a calculator
- Use the identities, limited to routine procedures:
tan θ= sinθ; sin2 θ + cos2θ = 1 ; 1 + tan2 θ = sec and cot2 θ + 1 cosec2θ
cosθ - Apply reduction formulae (180º±θ) and (360º±θ)
- Determine the solutions of trigonometric equations for θ∈[0º;360º] limited to routine procedures
- Apply sine, cosine and area rules (proofs of these rules will not be examined)
- Apply trigonometric identities studied in earlier grades to prove that left hand side equals to right hand side
- Solve problems in two and three dimensions by constructing and interpreting geometric and trigonometric models. Only angles and numerical distances/lengths should be used.
- Determine effects of the parameters on the functions defined by:
y = asin x + q , y = acos x + q, y = sin(ax) , y = cos(ax) and y = a tan x - Determine the effects of p on the functions defined by:
y = sin(x + p) , y = cos(x + p) and y = tan(x + p)
NOTE: One parameter should be tested at a time when examining horizontal shift.
- ACCEPTABLE REASONS: EUCLIDEAN GEOMETRY
In order to have some kind of uniformity, the use of the following shortened versions of the theorem statements is encouraged.THEOREM STATEMENT ACCEPTABLE REASON(S) LINES The adjacent angles on a straight line are supplementary. ∠s on a str line If the adjacent angles are supplementary, the outer arms of these angles form a straight line. adj ∠s supp The adjacent angles in a revolution add up to 360°. ∠s round a pt OR ∠s in a rev Vertically opposite angles are equal. vert opp ∠s = If AB || CD, then the alternate angles are equal. alt ∠s; AB || CD If AB || CD, then the corresponding angles are equal. corresp ∠s; AB || CD If AB || CD, then the co-interior angles are supplementary. co-int ∠s; AB || CD If the alternate angles between two lines are equal, then the lines are parallel. alt ∠s = If the corresponding angles between two lines are equal, then the lines are parallel. corresp ∠s = If the co-interior angles between two lines are supplementary,
then the lines are parallel.co-int ∠s supp TRIANGLES The interior angles of a triangle are supplementary. ∠ sum in Δ OR sum of ∠s in Δ
OR Int ∠s ΔThe exterior angle of a triangle is equal to the sum of the interior opposite angles. ext ∠ of Δ The angles opposite the equal sides in an isosceles triangle are equal. ∠s opp equal sides The sides opposite the equal angles in an isosceles triangle are equal. sides opp equal ∠s In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Pythagoras OR
Theorem of PythagorasIf the square of the longest side in a triangle is equal to the sum of the squares of the other two sides then the triangle is right-angled. Converse Pythagoras
OR
Converse Theorem of PythagorasIf three sides of one triangle are respectively equal to three sides of another triangle, the triangles are congruent. SSS If two sides and an included angle of one triangle are respectively equal to two sides and an included angle of another triangle, the triangles are congruent. SAS OR S∠S If two angles and one side of one triangle are respectively equal to two angles and the corresponding side in another triangle, the triangles are congruent. AAS OR ∠∠S If in two right-angled triangles, the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of the other, the triangles are congruent RHS OR 90°HS The line segment joining the midpoints of two sides of a triangle is parallel to the third side and equal to half the length of the third side Midpt Theorem THEOREM STATEMENT ACCEPTABLE REASON(S) The line drawn from the midpoint of one side of a triangle, parallel to another side, bisects the third side. line through midpt || to 2nd side A line drawn parallel to one side of a triangle divides the other two sides proportionally. line || one side of Δ
OR
prop theorem; name || linesIf a line divides two sides of a triangle in the same proportion, then the line is parallel to the third side. line divides two sides of Δ in prop If two triangles are equiangular, then the corresponding sides are in proportion (and consequently the triangles are similar). ||| Δs OR equiangular Δs If the corresponding sides of two triangles are proportional, then the triangles are equiangular (and consequently the triangles are similar). Sides of Δ in prop If triangles (or parallelograms) are on the same base (or on bases of equal length) and between the same parallel lines, then the triangles (or parallelograms) have equal areas. same base; same height OR
equal bases; equal heightCIRCLES The tangent to a circle is perpendicular to the radius/diameter of the circle at the point of contact. tan ⊥ radius tan ⊥ diameter If a line is drawn perpendicular to a radius/diameter at the point where the radius/diameter meets the circle, then the line is a tangent to the circle. line ⊥ radius OR converse tan ⊥ radius OR converse tan ⊥ diameter The line drawn from the centre of a circle to the midpoint of a chord is perpendicular to the chord. line from centre to midpt of chord The line drawn from the centre of a circle perpendicular to a chord bisects the chord. line from centre ⊥ to chord The perpendicular bisector of a chord passes through the centre of the circle; perp bisector of chord The angle subtended by an arc at the centre of a circle is double the size of the angle subtended by the same arc at the circle (on the same side of the chord as the centre) ∠ at centre = 2 ×∠ at circumference The angle subtended by the diameter at the circumference of the circle is 90°. ∠s in semi- circle OR
diameter subtends right angleIf the angle subtended by a chord at the circumference of the circle is 90°, then the chord is a diameter. chord subtends 90° OR
converse ∠s in semi -circleAngles subtended by a chord of the circle, on the same side of the chord, are equal ∠s in the same seg. If a line segment joining two points subtends equal angles at two points on the same side of the line segment, then the four points are concyclic. line subtends equal ∠s OR
converse ∠s in the same seg.Equal chords subtend equal angles at the circumference of the circle. equal chords; equal ∠s Equal chords subtend equal angles at the centre of the circle. equal chords; equal ∠s THEOREM STATEMENT ACCEPTABLE REASON(S) Equal chords in equal circles subtend equal angles at the centre of the circles. equal circles; equal chords; equal ∠s The opposite angles of a cyclic quadrilateral are supplementary opp ∠s of cyclic quad If the opposite angles of a quadrilateral are supplementary then the quadrilateral is cyclic. opp ∠s quad supp OR
converse opp ∠s of cyclic quadThe exterior angle of a cyclic quadrilateral is equal to the interior opposite angle. ext ∠ of cyclic quad If the exterior angle of a quadrilateral is equal to the interior opposite angle of the quadrilateral, then the quadrilateral is cyclic. ext ∠ = int opp ∠ OR
converse ext ∠ of cyclic quadTwo tangents drawn to a circle from the same point outside the circle are equal in length Tans from common pt OR
Tans from same ptThe angle between the tangent to a circle and the chord drawn from the point of contact is equal to the angle in the alternate segment. tan chord theorem If a line is drawn through the end-point of a chord, making with the chord an angle equal to an angle in the alternate segment, then the line is a tangent to the circle. converse tan chord theorem OR
∠ between line and chordQUADRILATERALS The interior angles of a quadrilateral add up to 360°. sum of ∠s in quad The opposite sides of a parallelogram are parallel. opp sides of ||m If the opposite sides of a quadrilateral are parallel, then the quadrilateral is a parallelogram. opp sides of quad are || The opposite sides of a parallelogram are equal in length. opp sides of ||m If the opposite sides of a quadrilateral are equal, then the quadrilateral is a parallelogram. opp sides of quad are =
OR
converse opp sides of a parmThe opposite angles of a parallelogram are equal. opp ∠s of ||m If the opposite angles of a quadrilateral are equal then the quadrilateral is a parallelogram. opp ∠s of quad are = OR
converse opp angles of a parmThe diagonals of a parallelogram bisect each other. diag of ||m If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. diags of quad bisect each other
OR
converse diags of a parmIf one pair of opposite sides of a quadrilateral are equal and parallel, then the quadrilateral is a parallelogram. pair of opp sides = and || The diagonals of a parallelogram bisect its area. diag bisect area of ||m The diagonals of a rhombus bisect at right angles. diags of rhombus The diagonals of a rhombus bisect the interior angles. diags of rhombus All four sides of a rhombus are equal in length. sides of rhombus All four sides of a square are equal in length sides of square The diagonals of a rectangle are equal in length. diags of rect The diagonals of a kite intersect at right-angles. diags of kite A diagonal of a kite bisects the other diagonal. diag of kite A diagonal of a kite bisects the opposite angles diag of kite - INFORMATION SHEET:TECHNICAL MATHEMATICS
- GENERAL GUIDELINES FOR MARKING
- If a learner makes more than one attempt at answering a question and does not cancel any of them out, only the first attempt will be marked irrespective of which of the attempts may be the correct answer.
- Consistent accurate marking regarding calculations will be followed in the following cases:
- Subquestion to subquestion: When a certain variable is incorrectly calculated in one subquestion and needs to be substituted into another subquestion, full marks can be awarded for the subsequent subquestions provided the methods used are correct and the calculations are correct.
- Assuming values/answers to solve a problem is unacceptable.
- CONCLUSION
This examination Guidelines document is meant to articulate the assessment aspirations embraced in the CAPS document. It is therefore not a substitute for the CAPS document which teachers should teach to.
Qualitative curriculum coverage as clarified in the CAPS cannot be overemphasised.