GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2017
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 2
GRADE 12
NOVEMBER 2017
NATIONAL SENIOR CERTIFICATE
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions in the ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTION 1
The table below shows the time (in seconds, rounded to ONE decimal place) taken by 12 athletes to run the 100 metre sprint and the distance (in metres, rounded to ONE decimal place) of their best long jump.
| Time for 100 m sprint (in seconds) | 10,1 | 10,2 | 10,5 | 10,9 | 11 | 11,1 | 11,2 | 11,5 | 12 | 12 | 12,2 | 12,5 |
| Distance of best long jump (in metres) | 8 | 7,7 | 7,6 | 7,3 | 7,6 | 7,2 | 6,8 | 7 | 6,6 | 6,3 | 6,8 | 6,4 |
The scatter plot representing the data above is given below.

The equation of the least squares regression line is 5, = a+ bx.
1.1 Determine the values of a and b.(3)
1.2 An athlete runs the 100 metre sprint in 11,7 seconds. Use .1) = a + bx to predict the distance of the best long jump of this athlete. (2)
1.3 Another athlete completes the 100 metre sprint in 12,3 seconds and the distance of his best long jump is 7,6 metres. If this is included in the data, will the gradient of the least squares regression line increase or decrease? Motivate your answer without any further calculations. (2)
[7]
QUESTION 2
In an experiment, a group of 23 girls were presented with a page containing 30 coloured rectangles. They were asked to name the colours of the rectangles correctly as quickly as possible. The time, in seconds, taken by each of the girls is given in the table below.
| 12 | 13 | 13 | 14 | 14 | 16 | 17 | 18 | 18 | 18 | 19 | 20 |
| 21 | 21 | 22 | 22 | 23 | 24 | 25 | 27 | 29 | 30 | 36 |
2.1 Calculate:
2.1.1 The mean of the data (2)
2.1.2 The interquartile range of the data (3)
2.2 The standard deviation of the times taken by the girls is 5,94. How many girls took longer than ONE standard deviation from the mean to name the colours?(2)
2.3 Draw a box and whisker diagram to represent the data on the number line provided in the ANSWER BOOK. (3)
2.4 The five-number summary of the times taken by a group of 23 boys in naming the colours of the rectangles correctly is (15 ; 21 ; 23,5 ; 26 ; 38).
2.4.1 Which of the two groups, girls or boys, had the lower median time to correctly name the colours of the rectangles? (1)
2.4.2 The first three learners who named the colours of all 30 rectangles correctly in the shortest time will receive a prize. How many boys will be among these three prizewinners? Motivate your answer. (2)
[13]
QUESTION 3
In the diagram, A, B(-6 ; —5) and C(8 ; —4) are points in the Cartesian plane. F (3; 3½) and G are points on line AC such that AF = FG. E is the x-intercept of AB.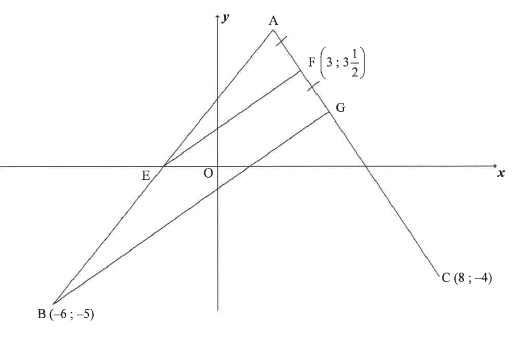
3.1 Calculate:
3.1.1 The equation of AC in the form y = mx + c (4)
3.1.2 The coordinates of G if the equation of BG is 7x — 1 Oy = 8 (3)
3.2 Show by calculation that the coordinates of A is (2 ; 5).(2)
3.3 Prove that EF II BG. (4)
3.4 ABCD is a parallelogram with D in the first quadrant. Calculate the coordinates of D.(4)
[17]
QUESTION 4
In the diagram, P(-4 ; 5) and K(0 ; —3) are the end points of the diameter of a circle with centre M. S and R are respectively the x- and y-intercept of the tangent to the circle at P, θ is the inclination of PK with the positive x-axis.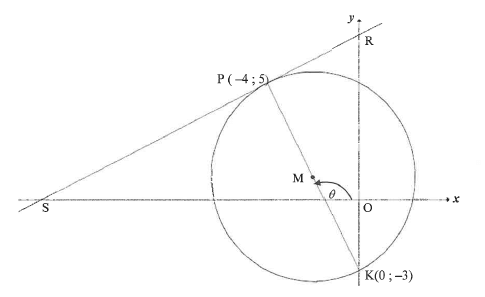
4.1 Determine:
4.1.1 The gradient of SR(4)
4.1.2 The equation of SR in the form y = mx + c(2)
4.1.3 The equation of the circle in the form (x — a)2 + (y —b)2(4)
4.1.4 The size of PKR(3)
4.1.5 The equation of the tangent to the circle at K in the form y = mx + c(2)
4.2 Determine the values of t such that the line y =½ x + r cuts the circle at two different points(3)
4.3 Calculate the area of ASMK. (5)
[23]
QUESTION 5
5.1 Given: sin(A — 360°).cos(90° + A)
cos(90° — A).tan(—A)
Simplify the expression to a single trigonometric ratio.(6)
5.2 In the diagram, P(3 ; t) is a point in the Cartesian plane. OP = √34 and HOP = β is a reflex angle.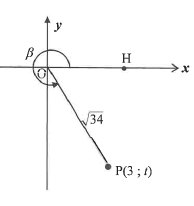
Without using a calculator, determine the value of:
5.2.1 t (2)
5.2.2 tan β (1)
5.2.3 cos 2β (4)
5.3 Prove:
5.3.1 sin(A + B)— sin(A — B) = 2 cos A. sin B (2)
5.3.2 Without using a calculator, that sin 77° — sin 43° = sin17°(4)
QUESTION 6
In the diagram, the graph of f (x) = cos 2x is drawn for the interval x E [-270°; 90]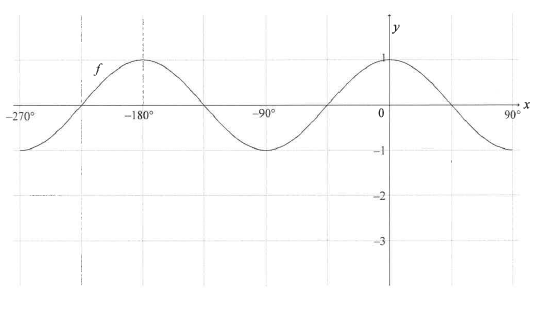
6.1 Draw the graph of g(x) = 2 sin x —1 for the interval x∈ [-270° ; 90°] on the grid given in your ANSWER BOOK. Show ALL the intercepts with the axes, as well as the turning points. (4)
6.2 Let A be a point of intersection of the graphs of f and g. Show that the x-coordinate of A satisfies the equation sin x = -1 + √5 (4)
2
6.3 Hence, calculate the coordinates of the points of intersection of graphs off and g for the interval x ∈ [-270°; 90°]. (4)
[12]
QUESTION 7
AB represents a vertical netball pole. Two players are positioned on either side of the netball pole at points D and E such that D, B and E are on the same straight line. A third player is positioned at C. The points B, C, D and E are in the same horizontal plane. The angles of elevation from C to A and from E to A are x and y respectively. The distance from B to E is k.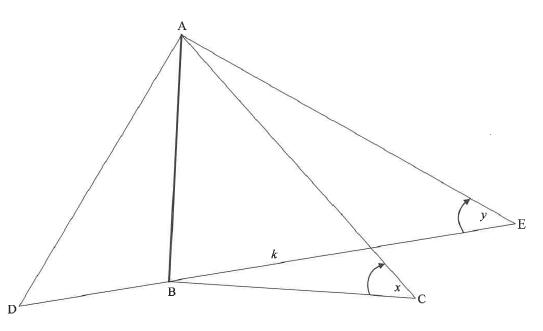
7.1 Write down the size of ABC. (1)
7.2 Show that AC = k.tan y (4)
sin x
7.3 If it is further given that DAC = 2x and AD = AC, show that the distance DC between the players at D and C is 2k tan y (5)
[10]
Give reasons for your statements in QUESTIONS 8, 9, 10 and 11.
QUESTION 8
In the diagram, points A, B, D and C lie on a circle. CE ll AB with E on AD produced. Chords CB and AD intersect at F. D2 = 50° and C1 = 15°.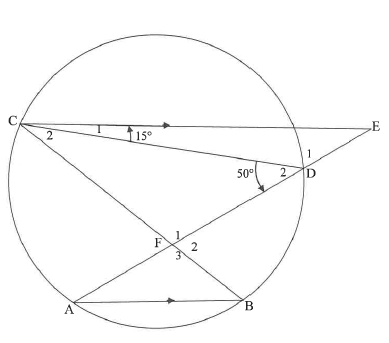
8.1 Calculate, with reasons, the size of:
8.1.1 A (3)
8.1.2 C2 (2)
8.2 Prove, with a reason, that CF is a tangent to the circle passing through points C, D and E. (2)
QUESTION 9
In the diagram, AABC and LACD are drawn. F and G are points on sides AB and AC respectively such that AF = 3x, FB = 2x, AG = 12y and GC = 8y. H, E and K are points on side AD such that GH II CK and GE II CD.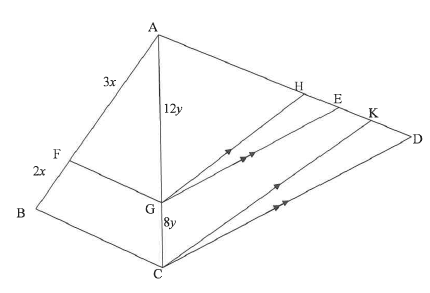
9.1 Prove that:
9.1.1 FG II BC (2)
9.1.2 AH = AE
HK ED
9.2 If it is further given that AH = 15 and ED = 12, calculate the length of EK. (5)
[10]
QUESTION 10
In the diagram, W is a point on the circle with centre 0. V is a point on OW. Chord MN is drawn such that MV = VN. The tangent at W meets OM produced at T and ON produced at S.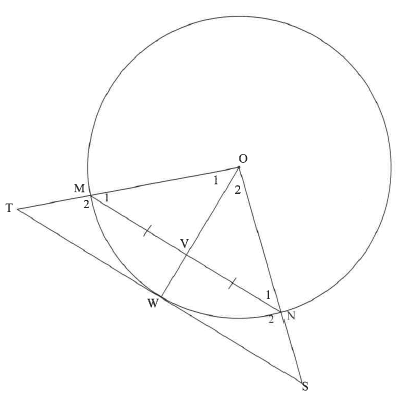
10.1 Give a reason why OV 1 MN.(1)
10.2 Prove that:
10.2.1 MN II TS (2)
10.2.2 TMNS is a cyclic quadrilateral (4)
10.2.3 OS . MN = 20N . WS (5)
[12]
QUESTION 11
11.1 In the diagram, chords KM, MN and KN are drawn in the circle with centre O. PNQ is the tangent to the circle at N.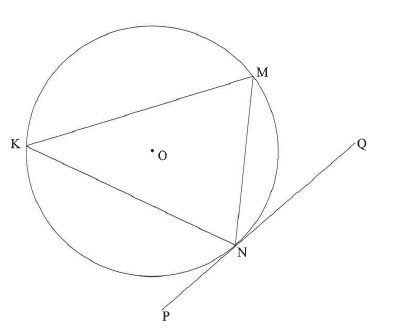
Prove the theorem which states thats MNQ=K
11.2 In the diagram, BC is a diameter of the circle. The tangent at point D on the circle meets CB produced at A. CD is produced to E such that EA ⊥ AC. BD is drawn.
Let C = x.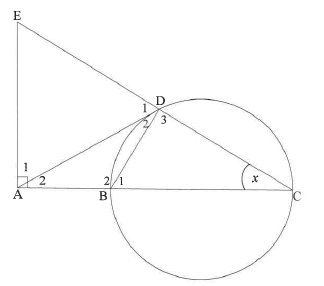
11.2.1 Give a reason why:
- D3 = 90° (1)
- ABDE is a cyclic quadrilateral (1)
- D2 = x (1)
11.2.2 Prove that:
- AD = AE (3)
- ΔADB III ΔACD (3)
11.2.3 It is further given that BC = 2AB = 2r.
- Prove that AD2 = 3r2 (2)
- Hence, prove that AADE is equilateral. (4)
[20]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS