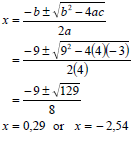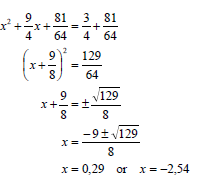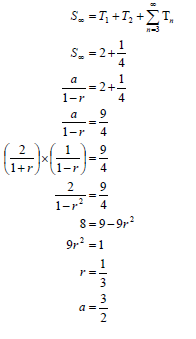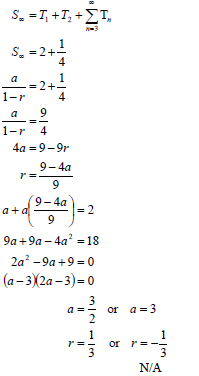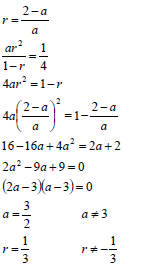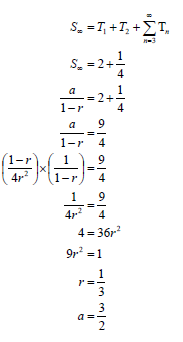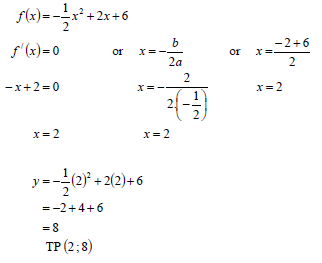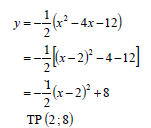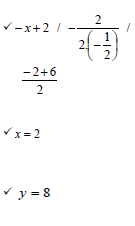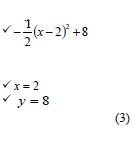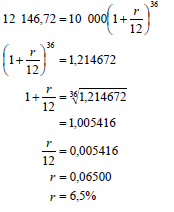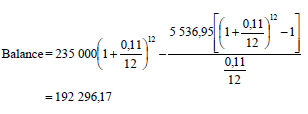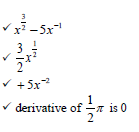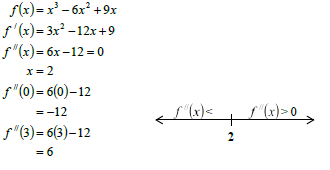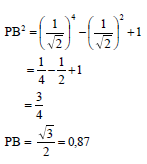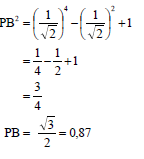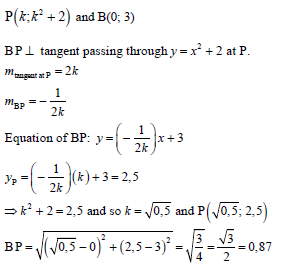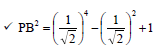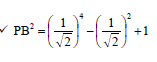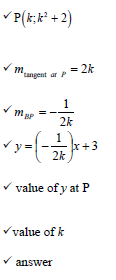GRADE 12 MATHEMATICS PAPER 1 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2017
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 1
GRADE 12
NOVEMBER 2017
MEMORANDUM
NATIONAL SENIOR CERTIFICATE
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- Consistent accuracy applies in ALL aspects of the marking guidelines. Stop marking at the second calculation error.
QUESTION 1
1.1.1 | x2 + 9x + 14 = 0 | ✓ factors (3) |
1.1.2 | 4x2 + 9x - 3 = 0 OR | ✓ substitution
✓ simplification ✓ x = 0,29 ✓ x = - 2,54
OR
✓ for adding 81 on both sides ✓ simplification ✓ x = 0,29 ✓ x = - 2,54 (4) |
1.1.3 | √x 2 - 5 = 2√x | ✓ x2 - 5 = 4x |
1.2 | 3x - y = 4 OR 3x - y = 4 | ✓ y subject of formula ✓ substitution ✓ correct standard form ✓ factors ✓ x-values ✓ y-values
OR ✓ x subject of formula ✓ substitution ✓ correct standard form ✓ factors ✓ y-values ✓ x-values (6) |
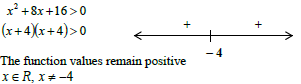
1.3.1 | x 2 + 8x + 16 > 0 OR | ✓ (x + 4)(x + 4)
OR ✓ (x + 4)(x + 4) (3) |
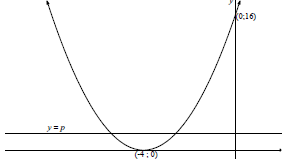
1.3.2 | For two negative unequal roots: 0 < p < 16 OR x2 + 8x + 16 = p OR x = - 8 ± √64 - 4(16 - p)
OR For both roots to be negative : | ✓0 ✓ 16
✓✓ 0 < p < 16 (4)
OR
✓ 0 ✓ 16 ✓✓ 0 < p < 16 (4)
✓ 0 ✓ 16 ✓✓ 0 < p < 16 (4)
✓ 0 ✓ 16 ✓✓ 0 < p < 16 (4) [24] |
QUESTION 2
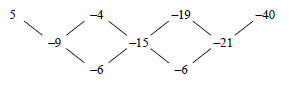
2.1.1 | first differences: –9; –15; –21 | ✓ first differences ✓ – 6 (2) | |
2.1.2 | Tn = an2 + bn + c a = second difference = -3 3a + b = -9 OR (n - 1)(n - 2)d Tn = T1 + (n - 1)d1 + (n - 1)(n - 2)d2 | ✓ a = -3 ✓ b = 0 ✓ c = 8 ✓ Tn = -3n2 + 8
OR
✓ a = -3 ✓ b = 0 ✓ c = 8 ✓ Tn = -3n2 + 8 (4) | |
2.1.3 | - 3n2 + 8 = -25 939 | ✓ Tn = -25 939 ✓ n2 = 8649 ✓ answer (3) | |
2.2.1 | 2k - 7 ; k + 8 and 2k -1 | ✓ k + 8 - (2k - 7) = 2k -1- (k + 8) ✓ k = 12 ✓ 17 ✓ d = 3 ✓ T15 = 59 (5) |
2.2.2 | Sequence is 17 ; 20 ; 23 ; 26 ; 29 ; 32 ……. OR | ✓ 20 + 26 + 32 + ....... ✓ a = 20 d = 6 ✓ subst into correct formula ✓ answer (4) ✓ a = 20 d = 6 ✓ T30 = 94 ✓ S30 = 30 (20 + 194) [18] |
QUESTION 3
| 3.1 | a + ar = 2 OR a - 2 = 1 OR 2 = a(r 2 -1) 2 = a(r -1)(r +1) OR ar 2 = 1 | ✓ a + ar = 2 ✓ a = 2 ✓ a - 2 = 1 ✓ a = 9 - 9r
OR ✓ 2 = a(r 2 -1) ✓ a = 2 ✓ ar 2 = 1 ✓ a = 1- r |
3.2 |
OR OR | ✓ S∞ = 2 + 1 ✓ substitution of a into the correct formula ✓ 9r 2 = 1 (6) OR ✓ S = 2 + 1 ✓ substitution of a into the correct formula OR ✓ r = 2 - a ✓ (2a - 3)(a - 3) = 0 ✓ a = 3 OR ✓ S∞ = 2 + 1 |
QUESTION 4
4.1 | f (x) = -ax2 + bx + 6 f (- 1) = 7
OR | ✓ – 2ax + b ✓✓ 2a + b = 3 ✓ - a - b + 6 = 7 ✓ solve simultaneously (5)
✓ – 2ax + b (5) |
4.2 | f (x) = - ½ x 2 + 2x + 6 | ✓ - ½ x2 + 2x + 6 = 0 |
4.3 | OR
|
OR
|
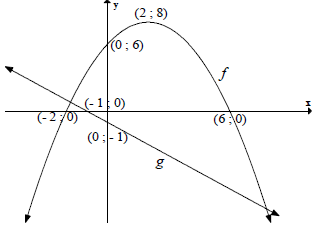
4.4 4.6 |
| 4.4: 4.6: |
| 4.5 | 0<x<4 or (0;4) | ✓ 4 ✓✓ 0<x<4 (3) |
4.7 | x ≤ -2 or - 1 ≤ x ≤ 6 OR/OF (-∞ ; - 2] or [-1; 6] | ✓ x ≤ -2 ✓✓ - 1 ≤ x ≤ 6 (3) [23] |
5.1 | y ∈ R ; y ≠ -1 | ✓✓ answer (2) |
5.2 | D(2 ; - 1) | ✓ D(2 ; - 1) |
| 5.3 | f(x) = log3x OR | ✓ correct substitution of A ✓✓ t = 3 (3) |
5.4 | x = log3 y | ✓ interchange x and y |
5.5 | 3x < 31 OR | ✓ 3x < 31 |
5.6 | Equation of the axis of symmetry: y = -x + 1 OR | ✓✓equation of axis of symmetry ✓ B or (1 ; 0) OR ✓✓ BE = ED = 1 |
QUESTION 6
6.1 | A = P(1 + i)n | ✓ r ✓ correct substitution into formula ✓ 1 +r = 36√36 1,214672 |
6.2.1 | 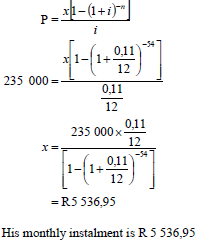 | ✓ i = 0,11 12 ✓ n = 54 ✓ correct substitution in P ✓ answer (4) |
6.2.2 | Amount paid for the year : (5 536,95´12) = R 66 443,40 Interest = (5 536,95´12)- (235 000 -192 296,17) OR OR | ✓ R 66 443,40 OR ✓ R 66 443,40 OR ✓ 235 000 – 192 296,17 [15]
|
QUESTION 7
7.1 | f (x + h) = 2(x + h)2 - (x + h) OR f / (x) = lim f (x + h) - f (x) = lim 2 x2 + 4xh + 2h2 - x - h - 2x2 + x | ✓ 2x2 + 4xh + 2h 2 - x - h
OR |
7.2.1 | Dx[(x + 1)(3x - 7)] | ✓ 3x2 - 4x - 7 |
7.2.2 | 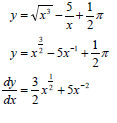 | [12] |
QUESTION 8
8.1 |
| ✓ x3 - 6x2 + 9x ✓ 3x 2 -12x + 9 ✓ 6x -12 ✓ 6x -12 = 0 ✓ explanation (5) |
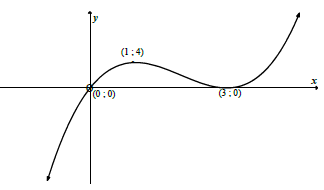
8.2 | ✓ shape ✓ (0 ; 0) ✓ (3 ; 0) as TP ✓ (1 ; 4) (4) | |
8.3 | f concave up for x > 2 | ✓✓ x > 2 (2) |
8.4.1 | (3;7) | ✓ 3 ✓ 7 (2) |
8.4.2 | Do not agree with Claire as her statement is incorrect. Between x = 1 OR | ✓ no ✓ justification (2) [15] |
QUESTION 9
y = x2 + 2
| ✓ (x - 0)2 + (x2 + 2 - 3)2 [7] |
QUESTION 10
10.1 | 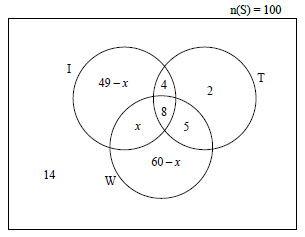 | 8 values need to be placed in correct position: 2 or 3 correct: 1 mark |
10.2 | (49 - x) + x + 8 + 4 + 5 + 2 + (60 - x) + 14 = 100 | ✓ setting up equation |
10.3 | P (use only one application) = 7 + 2 + 18 | ✓ 7 + 2 + 18 |
QUESTION 11
11.1 | 5 x 5 x 10 x 9 = 2250 | ✓ 5 x 5 | ||||||||||||||||||||||||
11.2 |
Codes of two letters and five digits will ensure unique numbers for 700 000 clients. | ✓ 5 x 5 x 10 x 9 x 8 x 7 x 6 |
TOTAL : 150