MATHEMATICS PAPER 1
GRADE 12
NOVEMBER 2017
NATIONAL SENIOR CERTIFICATE

INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of 11 questions.
2. Answer ALL the questions.
3. Number the answers correctly according to the numbering system used in this question paper.
4. Clearly show ALL calculations, diagrams, graphs et cetera that you have used in determining your answers.
5. Answers only will NOT necessarily be awarded full marks.
6. You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
7. If necessary, round off answers to TWO decimal places, unless stated otherwise.
8. Diagrams are NOT necessarily drawn to scale.
9. An information sheet with formulae is included at the end of the question paper.
10. Write neatly and legibly.

QUESTION 1
1.1 Solve for x:
1.1.1 x² + 9x +14 = 0
1.1.2 4x² + 9x — 3 = 0     (correct to TWO decimal places)
1.1.3 √x² - 5 = 2√x
1.2 Solve for x and y if: 3x - y = 4  and x² + 2xy - y² = -2
1.3 Given:  f (x) = x² + 8x + 16
1.3.1 Solve for x if f (x) > 0 . (3)
1.3.2 For which values of p will f (x) = p have TWO unequal negative roots? (4)
[24]

QUESTION 2
2.1 Given the following quadratic number pattern: 5 ; -4 ; -19 ; -40 ;
2.1.1 Determine the constant second difference of the sequence.(2)
2.1.2 Determine the n^th term (T_n) of the pattern. (4)
2.1.3 Which term of the pattern will be equal to =25 939? (3)
2.2 The first three terms of an arithmetic sequence are 2k - 7 ; k + 8 and   2k -1.
2.2.1 Calculate the value of the 15th term of the sequence. (5)
2.2.2 Calculate the sum of the first 30 even terms of the sequence. (4)
[18]

QUESTION 3
A convergent geometric series consisting of only positive terms has first term a, constant ratio r and n^th term, T_n , such that 
3.1 If T₁ + T₂ = 2 , write down an expression for a in terms of r.(2)
3.2 Calculate the values of a and r.(6)
[8]

QUESTION 4
Given: f(x) = -ax² +bx + 6
4.1 The gradient of the tangent to the graph of f at the point 
Show that a = ½ and b = 2.(5)
4.2 Calculate the x-intercepts of f(3)
4.3 Calculate the coordinates of the turning point of f.(3)
4.4 Sketch the graph of f . Clearly indicate ALL intercepts with the axes and the turning point.(4)
4.5 Use the graph to determine the values of x for which f (x) > 6.(3)
4.6 Sketch the graph of  g(x) = -x -1  on the same set of axes as f . Clearly indicate ALL intercepts with the axes.(2)
4.7 Write down the values of x for which f (x). g (x) 0 .(3)
[23]

QUESTION 5
The diagram below shows the graphs of g(x) =     2     + q and f(x) = log₃x
                                                                           x + p

• y = -1 is the horizontal asymptote of g.
• B(1 ; 0) is the x-intercept of f
• A(t ; 1) is a point of intersection between f and g.
• The vertical asymptote of g intersects the x-axis at E and the horizontal asymptote at D.
• OB = BE.

5.1 Write down the range of g. (2)
5.2 Determine the equation of g.(2)
5.3 Calculate the value of t. (3)
5.4 Write down the equation of f ^-1 , the inverse of f , in the form y =... (2)
5.5 For which values of x will f ^-1 (x) < 3? (2)
5.6 Determine the point of intersection of the graphs of f and the axis of symmetry of g that has a negative gradient. (3)

QUESTION 6
6.1 Mbali invested R10 000 for 3 years at an interest rate of  r % p.a., compounded monthly. At the end of this period, she received R12 146,72. Calculate  r, correct to ONE decimal place.(5)
6.2 Piet takes a loan from a bank to buy a car for R235 000. He agrees'to repay the loan over a period of 54 months. The first instalment will be paid one month after the loan is granted. The bank charges interest at 11% p.a., compounded monthly.
6.2.1 Calculate Piet's monthly instalment. (4)
6.2.2 Calculate the total amount of interest that Piet will pay during the first year of the repayment of the loan.(6)
[15]

QUESTION 7
7.1 Given:  f (x) = 2x² - x
Determine f' (x) from first principles. (6)
7.2 Determine:
7.2.1 D_x[(x + 1)(3x - 7)] (2)
7.2.2 dy if y = √x³ -  5  +  1  π(4)
         dx                   x       2

[12]

QUESTION 8
Given: f (x) = x(x — 3)² with f ^'(1) = t(3).= 0 and f (1) = 4
8.1 Show that f has a point of inflection at x = 2. (5)
8.2  Sketch the graph of f clearly indicating the intercepts with the axes and the turning points. (4)
8.3 For which values of x will y = - f (x) be concave down? (2)
8.4 Use your graph to answer the following questions:
8.4.1 Determine the coordinates of  the local maximum of  h if h(x) = f (x - 2)+ 3 . (2)
8.4.2 Claire claims that f'(2)=1.
Do you agree with Claire? Justify your answer.(2)
[15]

QUESTION 9
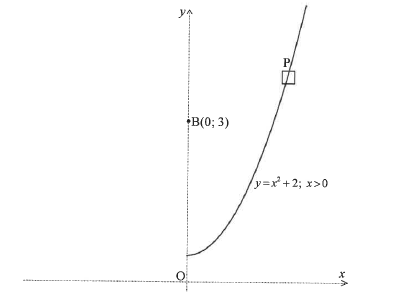
An aerial view of a stretch of road is shown in the diagram below. The road can be described by the function y = x² + 2 , x ≥ 0 if the coordinate axes (dotted lines) are chosen as shown in the diagram.
Benny sits at a vantage point B(0 ; 3) and observes a car, P, travelling along the road.

Calculate the distance between Benny and the car, when the car is closest to Benny.   [7]

QUESTION 10
A survey was conducted among        100 Grade    12 learners about their use of Instagram  (I), Twitter (T) and WhatsApp (W) on their cell phones. The survey revealed the following:

• 8 use all three.
• 12 use Instagram and Twitter.
• 5 use Twitter and WhatsApp, but not Instagram.
• x use Instagram and WhatsApp, but not Twitter.
• 61 use Instagram.
• 19 use Twitter.
• 73 use WhatsApp.
• 14 use none of these applications.

10.1 Draw a Venn diagram to illustrate the information above.(4)
10.2 Calculate the value of x.  (2)
10.3 Calculate the probability that a learner, chosen randomly, uses only ONE of these applications. (2)
[8]

QUESTION 11
A company uses a coding system to identify its clients. Each code is made up of two letters and a sequence of digits, for example AD108 or RR 45789.
The letters are chosen from A; D; R; S and U. Letters may be repeated in the code.
The digits 0 to 9 are used, but NO digit may be repeated in the code.
11.1 How many different clients can be identified with a coding system that is made up of TWO letters and TWO digits?  (3)
11.2 Determine the least number of digits that is required for a company to uniquely identify 700 000 clients using their coding system. (3)
[6]

TOTAL: 150

INFORMATION SHEET: MATHEMATICS