GRADE 12 MATHEMATICAL LITERACY PAPER 1 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2017
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICAL LITERACY PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2017
INSTRUCTIONS AND INFORMATION
- This question paper consists of FOUR questions. Answer ALL the questions.
- 2.1 Use the ANNEXURES in the ADDENDUM to answer the following questions:
ANNEXURE A for QUESTION 2.2
ANNEXURE B for QUESTION 4.1
ANNEXURE C for QUESTION 5.1 - Number the answers correctly according to the numbering system used in this question paper.
- Start EACH question on a NEW page.
- You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
- Show ALL calculations clearly.
- Round off ALL final answers appropriately according to the given context, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Maps and diagrams are NOT drawn to scale, unless stated otherwise.
- Write neatly and legibly.
QUESTION 1
1.1 Definitions of some mathematical concepts are listed in TABLE 1 below.
TABLE 1: DEFINITIONS OF SOME MATHEMATICAL CONCEPTS
| LETTER | DEFINITIONS |
| A | Middle value in an ordered data set |
| B | Difference between the maximum and minimum values in a data set |
| C | Distance from the centre of a circle to the circumference of the circle |
| D | Positive difference between the income and the expenditure amounts |
| E | Maximum distance between two points on the circumference of a circle |
| F | Amount received from the sale of goods or services |
| G | Sum of the data values divided by the number of data values |
Use TABLE 1 to select the definition for EACH of the following concepts. NOTE: Write down only the letter (A—G) of the correct definition.
1.1.1 Profit (2)
1.1.2 Mean (2)
1.1.3 Length of the radius (2)
1.2 A gold coin shop buys and sells gold Krugerrand coins.The shop bought a one-ounce gold coin for R14 960 at 10:15 and sold it for R18 700
5 hours and 50 minutes later.
1.2.1 Calculate the profit that the shop made on this one-ounce gold coin.(2)
1.2.2 Write down the exact time when the coin was sold. (2)
1.2.3 The diameter of a one-ounce gold coin is 32,8 mm. A gold coin is placed in the centre of a square box of side length 71,8 mm, as shown below.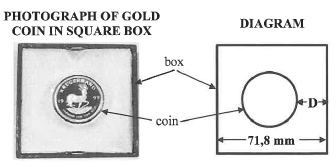
- Calculate the length of the radius of the coin. (2)
- Determine the shortest distance (D) between the edge of the coin and the side of the square box. (2)
1.3
Naomi buys a 2 f bottle of concentrated juice. |  |
1.3.1 Calculate the cost per litre of the diluted juice. (2)
1.3.2 Determine, in simplified form, the ratio of:
volume of concentrated juice: volume of water (2)
1.3.3 Determine the exact number of glasses of diluted juice that can be served. (2)
1.4 TABLE 2 below shows the mean monthly rainfall (in mm) and the mean number of rainy days per month for two South African cities.
TABLE 2: MEAN MONTHLY RAINFALL AND MEAN NUMBER OF RAINY DAYS PER MONTH FOR KIMBERLEY AND DURBAN
| MONTH | MEAN MONTHLY RAINFALL (mm) | MEAN NUMBER OF RAINY DAYS | ||
| DURBAN | KIMBERLEY | DURBAN | KIMBERLEY | |
| January | 126 | 93 | 10 | 7 |
| February | 142 | 81 | 9 | 7 |
| March | 120 | 88 | 9 | 7 |
| April | 60 | 68 | 6 | 6 |
| May | 39 | 6 | 4 | 2 |
| June | 35 | 6 | 3 | 1 |
| July | 39 | 3 | 3 | 1 |
| August | 63 | 9 | 5 | 1 |
| September | 84 | 18 | 7 | 2 |
| October | 107 | 27 | 10 | 4 |
| November | 117 | 39 | 12 | 5 |
| December | 93 | 83 | 10 | 6 |
Use TABLE 2 above to answer the questions that follow.
1.4.1 Arrange the mean monthly rainfall for Durban in ascending order. (2)
1.4.2 In which month does Kimberley receive the lowest mean monthly rainfall? (2)
1.4.3 Write down the modal number of rainy days for the first six months of the year for Durban.(2)
1.4.4 In which month does Kimberley have a higher mean monthly rainfall than Durban? (2)
1.4.5 During which month(s) is the mean monthly rainfall in Durban the same? (2)
[30]
QUESTION 2
2.1 TABLE 3 below shows the bus fare (in rand), including 14% VAT, for a single trip.
TABLE 3: BUS FARE IN RAND FOR A SINGLE TRIP
| Port Elizabeth | Grahamstown | King William's Town | Queenstown | Aliwal North | Bloemfontein | Welkom | |
| Port Elizabeth | 305 | 320 | 395 | 410 | 435 | 515 | |
| Grahamstown | 305 | 305 | 385 | 410 | 435 | 515 | |
| King William's Town | 320 | 305 | 350 | 410 | 435 | 465 | |
| Queenstown | 395 | 385 | 350 | 365 | 410 | 455 | |
| Aliwal North | 410 | 410 | 410 | 365 | 410 | 435 | |
| Bloemfontein | 435 | 435 | 435 | 410 | 410 | 335 | |
| Welkom | 515 | 515 | 465 | 455 | 435 | 335 |
Use TABLE 3 above to answer the questions that follow.
2.1.1 Write down the SECOND highest bus fare for a single trip between two cities. (2)
2.1.2 Between which two cities is the single bus fare R350,00? (2)
2.1.3 A person travels from Port Elizabeth to Bloemfontein via another city, City X, and uses two different buses. The total cost for this one-way trip is R755.
- Calculate the cost from Port Elizabeth to City X. (2)
- Hence, identify City X. (2)
2.1.4 Determine the cost, excluding 14% VAT, of a single bus fare of R365,00. (3)
2.1.5 Lindiwe travels from Queenstown to Bloemfontein and back once a month.
Calculate her total return travelling cost for ONE year. (4)
2.2 ANNEXURE A shows an adapted municipal account statement (property rates and services account) of Mr Fortune.
Use ANNEXURE A to answer the questions that follow.(2)
2.2.1 Write down the valuation date (month and year) of Mr Fortune's property.(2)
2.2.2 Name the municipal services that Mr Fortune is charged for.(2)
2.2.3 Determine the end date of the reading period of this statement.(2)
2.2.4 Show how the daily average water consumption of 0,522 kf was calculated.(2)
2.2.5 Name and explain which service on this statement is a variable expense.(3)
2.2.6 Determine the missing value:
- A (2)
- B (2)
2.2.7 Calculate the monthly sewerage rate (excluding 14% VAT) per square metre for this property.(2)
2.2.8 Write down the unpaid amount for December 2016.(2)
2.2.9 Mr Fortune paid R1 800 on 15 January 2017.
Name the type of rounding he used to obtain this amount.(2)
2.3 Rajesh exchanged a gift of £360,00 to South African rand at a bank.
The exchange rate was R1,00 = £0,05773.
The bank charged 1,95% commission on the amount exchanged.
Rajesh then invested R5 000 of his gift in a fixed deposit account for 1½ years at a compound interest rate of 6,3%, per annum.
2.3.1 Calculate (in pounds) the amount of commission Rajesh paid.(2)
2.3.2 Convert £360,00 to rand.(3)
2.3.3 Calculate (without the use of a formula) the value of the fixed deposit at the end of 1½ years. Show ALL the steps of the calculation.(5)
QUESTION 3
3.1 Happy Life High School makes table centrepieces, each consisting of four balloons in a vase filled with sand, for the 2017 Ball. The school expects 240 people at the ball. Each table will accommodate a maximum of 8 people and ONE centrepiece will be placed on each table.
The diagrams below show the two types of centrepieces that will be used.
Dimensions of rectangular vase:
Length = 10 cm
Width = 6 cm
Height = 28 cm
Dimensions of cylindrical vase:
Diameter = 12 cm
Height= 28 cm
Use the information above to answer the questions that follow.
3.1.1 Calculate the minimum number of balloons required for all the centrepieces. (2)
3.1.2 Each vase will have a decorative ribbon around it. The ribbon will overlap 1 cm.
Calculate the minimum length of decorative ribbon needed to decorate ONE rectangular vase.
You may use the following formula:
Length of decorative ribbon (in cm) = 2 X (length + width) + 1 (3)
3.1.3 Calculate (in cm3) the volume of the cylindrical vase. You may use the following formula:
Volume of a cylinder = 7t X (radius)2 x height, using 7C = 3,142 (3)
3.1.4 The volume of the rectangular vase is 1 680 cm3.
- 45% of the vase will be filled with sand.
- The mass of 1 cm3 of sand is 1,53 g.
Calculate (in kg, rounded off to TWO decimal places) the mass of sand required for ONE rectangular vase. (4)
3.2 The ladies attending the ball will each receive a triangular-shaped gift box. The box is made up of three identical rectangular faces and two identical triangular faces, as shown in the diagrams below. Each box will be covered in gold foil.
Dimensions of rectangular faces:
- Length (/) = 6 cm
- Width (w) = 4 cm
Dimensions of triangular faces:
- Base (b) = 4 cm
- Height (h) = 3,464 cm
3.2.1 Calculate (in cm2) the area of ONE triangular face of the gift box. You may use the following formula:
Area of a triangle = ½ x base x height (3)
3.2.2 Hence, determine the total surface area (in cm2) of the box. You may use the following formula:
Total surface area of a triangular prism
= 2 x (area of triangular face) + 3 x length x width (4)
3.2.3 It takes 30 minutes to cover 20 boxes with foil.
Calculate (in seconds) the average time it will take to cover ONE box with foil. (2)
[21]
QUESTION 4
4.1 ANNEXURE B shows a route map and information regarding the 42,2 km 2017 Cape Town Marathon.
Use ANNEXURE B to answer the questions that follow.
4.1.1 Name the type of scale used for the route map.
4.1.2 What type of view is represented on this route map?
4.1.3 Name the general direction of the Groote Schuur Hospital (Tourist Attraction 10) from the starting point of the marathon.
4.1.4 Determine the exact number of medical help points located on the route.
4.1.5 Identify the suburbs in the vicinity of the halfway mark.
4.1.6 Identify the tourist attractions indicated on the map between the 15 km mark and the 20 km mark.
4.2 The diagrams below show a set of labelled assembly instructions (not in order of assembly) to build a toy car with Lego blocks.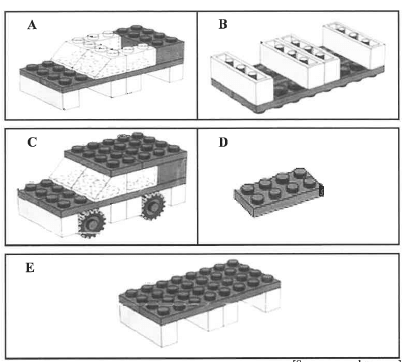
Study the diagrams above to answer the questions that follow.
4.2.1 Write down the correct order of the assembly instructions to build the toy car, using the letters A, B, C, D and E. (2)
4.2.2 Which letter (A, B, C, D or E) fits the instruction, 'Flip over the part-assembly'? (2)
4.2.3 A can of Lego blocks contains 20 red blocks, 25 blue blocks, 28 green blocks, 30 black blocks and 27 white blocks.
A block is randomly selected from the can.
Determine the probability that the block will be the following:
- Yellow (2)
- Blue (3)
4.2.4 The building blocks are packed into small cylindrical cans that are then packed into a large rectangular box, as shown in the diagrams below.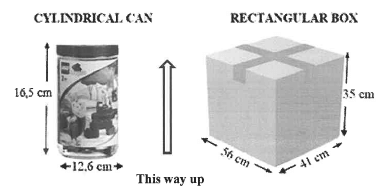
Dimensions of small cylindrical can:
Diameter = 12,6 cm
Height = 16,5 cm
Dimensions of large rectangular box:
Length = 56 cm
Width = 41 cm
Height = 35 cm
The cylindrical cans are placed upright in the box.
- Determine the number of layers of cans that can be placed in an upright position in the box. (2)
- Hence, determine the maximum number of cans that can be packed into ONE box. (3)
[27]
QUESTION 5
5.1 ANNEXURE C shows data relating to the 2015/2016 admissions for full-time NSC candidates for the 11 most common subjects.
All full-time candidates have to take at least seven subjects. Mathematics or Mathematical Literacy is compulsory.
Study the information in ANNEXURE C to answer the questions that follow.
5.1.1 Name another type of graphical representation that could be used to represent this data.(2)
5.1.2 Determine the maximum number of candidates who were admitted as full-time candidates in 2016.(2)
5.1.3 Determine the probability of randomly selecting a candidate, taking Mathematics or Mathematical Literacy, who was admitted in 2015.(2)
5.1.4 List ALL the subjects that showed a decrease in the number of full-time candidates admitted from 2015 to 2016.(2)
5.1.5 Name the subject that showed the greatest increase in the number of candidates admitted in 2016.(2)
5.1.6 Explain why this is called categorical data.(2)
5.1.7 Identify which subject in 2016 had more than two hundred twenty three thousand, but less than two hundred seventy four thousand candidates.(2)
5.2 The two pie charts, A and B, below represent the income and expenditure of all South African tertiary institutions.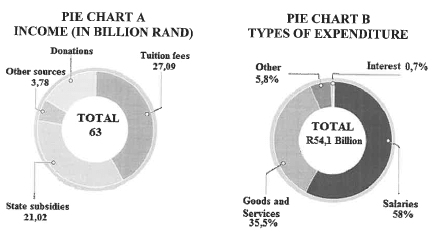
5.2.1 Give ONE example of an 'Other' type of expenditure applicable to tertiary institutions. (2)
5.2.2 What percentage of income comes from donations? (3)
5.2.3 Calculate the amount (in rand) of interest paid by tertiary institutions.(3)
5.2.4 Determine the difference (in millions of rand) between the income and expenditure of the tertiary institutions. (3)
[26]
TOTAL: 150