MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2018
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS
PAPER 1
GRADE 12
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2018
MEMORANDUM
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- Consistent accuracy applies in ALL aspects of the marking guidelines.
| QUESTION 1 | ||
1.1.1 | x2 - 6x - 16 = 0 | ✔ factors |
1.1.2 | 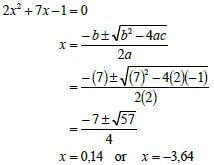 NOTE: Penalise 1 mark if the rounding to TWO decimal places is incorrect. | ✔subs into correct formula OR |
1.2 | 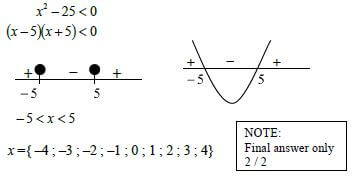 | ✔factors |
| 1.3 | x = 2y -1 OR
| ✔x = 2y −1 OR ✔ y = x + 1 |
| 1.4 | 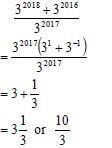 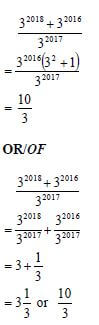 | ✔ common factor 32017 OR ✔ common factor 32016 OR ✔ dividing by 32017 |
| 1.5.1 | 3x - 5 ≥ 0 and x # 3 x ≥ 5/3 and x # 3 | ✔3x −5 ≥ 0 |
| 1.5.2 |  | ✔ √3x −5 = x −3 [26] |
| QUESTION 2 | ||
2.1.1 | 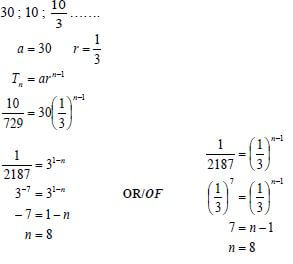 | ✔ r = 1/3 |
2.1.2 | S∞ = a | ✔substitution into correct formula |
2.2 | 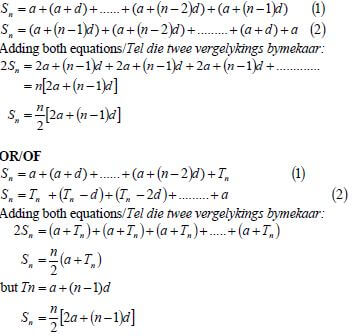 | ✔expandingn Sn [10] |
| QUESTION 3 | ||
3.1 | – 1 ; 2 ; 5 | ✔ 3n |
3.2 | T43 = 3(43) - 4 OR T43 = -1 + (43 - 1)(3) | ✔ subs of 43 |
3.3 | 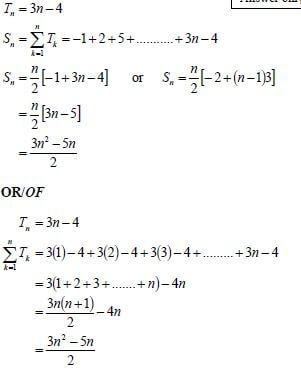 | 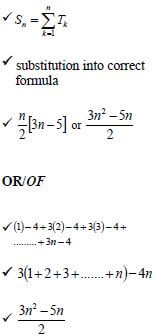 |
| 3.4 | T11 = (T11 - T10) + (T10 - T9) + (T9 - T8) + ..... + (T3 - T2) + (T2 - T1) + T1 NOTE: Answer only 1/6. OR Tn = an2 +bn + c | ✔✔ generating sum OR ✔121a +11b+c =125 [13] |
| QUESTION 4 | ||
4.1 | E(4 ; –9) | ✔ x = 4 |
4.2 | f(x) = (x - 4)2 - 9 OR f(x) = (x - 4)2 - 9 | ✔ y = 0 OR ✔ y = 0 |
4.3 | C(0 ;7) | ✔C(0 ;7) |
4.4 | C(0 ;7) | ✔D(4 ; 0) |
4.5 |
OR
| ✔ interchange x and y OR ✔ straight line through (0 ; 4) and ( 7 ; 0) |
| 4.6 | x . f (x) ≤ 0 | ✔✔x ≤ 0 [18] |
| QUESTION 5 | ||
5.1 | aº = 1 | ✔ x = 0 |
5.2 | g(x) = ax | ✔ substitution |
5.3 | y = (1/3)x or y = 3-x | ✔✔ y = (1/3)x (2) |
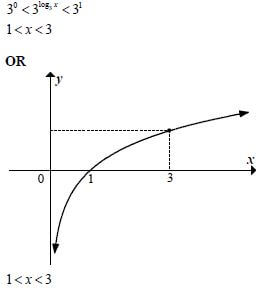
5.4 |
| ✔1< x OR ✔ 1 < x [8] |
| QUESTION 6 | ||
6.1 | q = 1 | ✔q =1 (1) |
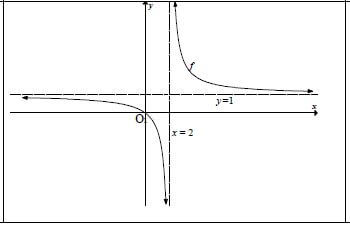
6.2 |
| ✔ 0 = a + 1 |
6.3 |
| ✔y = 1 [10] |
| QUESTION 7 | ||
7.1 |
| ✔ n = 60 and i = 0,06 / 0,005 |
7.2.1 | After eleven months, Genevieve will owe: | ✔ n = 11 |
7.2.2 |
| ✔ 94006,79 |
| 7.2.3 |  | ✔ n = - 083826912 OR
[16] |
| QUESTION 8 |
 |
| QUESTION 9 | ||
9.1 | f(x) = (x + 2)(x - 1)(x - 4) | ✔✔f (x) = (x + 2)(x −1)(x − 4) |
9.2 |
| ✔ f'(x) = 0 |
9.3 | f(x) = x3 - 3x2 - 6x + 8 f(-1) = (-1)3 - 3(-1)2 - 6(-1) + 8 or f(-1) = (1)(-2)(-5) = 10 = 10 f'(-1) = 3 (-1)2 - 6(-1) - 6 = 3 y - 10 = 3(x + 1) y = 3x + 13 | ✔f' (−1) =10 |
9.4 |
| ✔ f//(x) = 6x − 6 |
| 9.5 | f concave upwards NOTE: A nswer only 2/2 | ✔ f''(x) > 0 [17] |
| QUESTION 10 | ||
| 10 |  | |
| QUESTION 11 | ||
11.1.1 | Let the event Veli arrive late for school be V. | ✔ answer (1) |
11.1.2 | P(V or B) = P(V) +P(B) - P(V and B) | ✔ P(V or B) = P(V) +P(B) –P(V and B) |
11.1.3 | P(V) × P(B) = 0,25 × 0,2 | ✔P(V) × P(B) = 0,05 |
11.2.1 | 6 ! =720 | ✔6! or 720 (2) |
11.2.2 | Number of arrangements | ✔3!× 3! |
11.2.3 | P(hearts next to each other) = 3! × 4! OR P(hearts next to each other) = 4 × 3! × 3! | ✔ ✔3!× 4! OR ✔ ✔ [15] |
TOTAL: 150
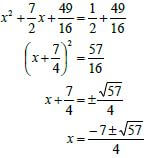
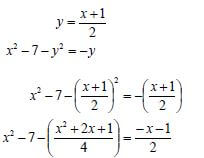
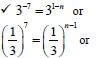
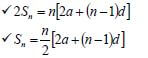 (4)
(4) 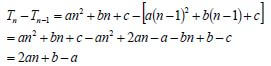
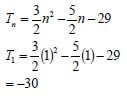
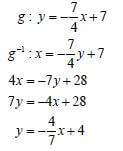


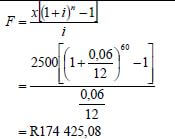
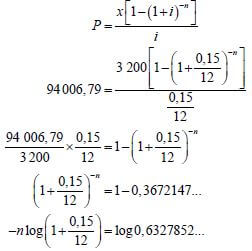
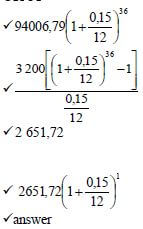 (5)
(5)