TECHNICAL MATHEMATICS PAPER 2
GRADE 12
NATIONAL SENIOR CERTIFICATE 
SEPTEMBER 2018

INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

Related Items

1. This question paper consists of 10 questions.
2. Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
3. Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining your answers.
4. Answers only will NOT necessarily be awarded full marks.
5. You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
6. If necessary, round off answers to TWO decimal places, unless stated otherwise.
7. Diagrams are not necessarily drawn to scale.
8. An information sheet with formulae is included at the end of the question paper.
9. Write neatly and legibly  

QUESTION 1
In the diagram below, the ellipse and straight line through A (0 ; 3) and B(– 2 ; 0) intersect at x and y intercepts respectively.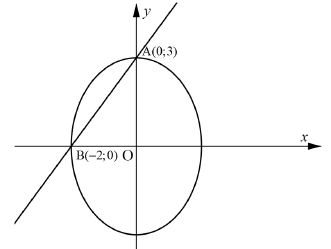

Determine:
1.1 The length of AB, rounded off to TWO decimal places (3)
1.2 The equation of line AB, in the form y = mx + c (4)
1.3 OÂB, correct to the nearest degree (3)
1.4 What type of triangle is ΔAOB? (1)
1.5 The equation of the ellipse, in the form x ² +   y ² = 1
                                                                    a²      b²          (3)
[14]

QUESTION 2
The following is a picture of grinding discs placed on top of each other.
The diagram next to it represent these discs with points A(-8;6) and B on the outer disc (larger circle), with centre at the origin.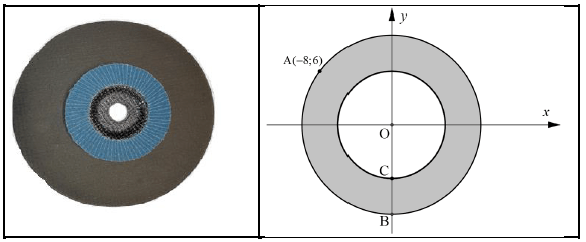
2.1 Determine the coordinates of B. (4)
2.2 If BC = 4 units, determine the equation of the smaller circle. (2)
2.3 Determine the equation of the tangent to the larger circle at A. (4)
[10]

QUESTION 3
3.1 Consider the diagram below. The positive angle between the x-axes and OP is θ. OP = 6,4 units and P(5; y) are given.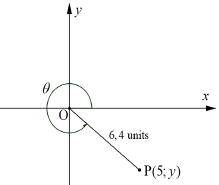

3.1.1 Determine the value of y, to the nearest integer. (4)
3.1.2 Determine the value of cotθ - cosecθ x sin²θ size. (5)
3.1.3 Determine the size of θ, rounded off to ONE decimal place. (4)
3.2 Simplify completely: sin(180º + x) tan(360º + x) cos(180º - x) (5)
3.3 Complete: 𝑠𝑒𝑐² 5x–1= … (1)
3.4 Solve for x∈ [0º;360º]:
2tan(x - 23º) + 5 = 0 (6)
[25]

QUESTION 4
The picture below represents a radio tower, supported by wires anchored on the ground. The diagram next to it represent this picture.
ACB is a flat piece of ground. HC is the tower 100 m in height. The tower is anchored with wires, at A and B. The distances between anchors A and B and the foot of the mast are 291 m and 261 m respectively. The angle of elevation from A to H is 24,5°.
ACB = 105º .
Calculate (Give your answers to the nearest integer):
4.1 The length of the wire that they must use to anchor the tower at A (i.e.: AH) (3)
4.2 The angle of elevation from B to H (i.e.: CB̂H) (3)
4.3 The length of AB, the distance between the two anchors (4)
4.4 The area of ΔABC (3)
[13]

QUESTION 5
Given f (x) = cos2x and g(x) = sin(x - 45º)
Study the given graphs below and answer the questions that follows.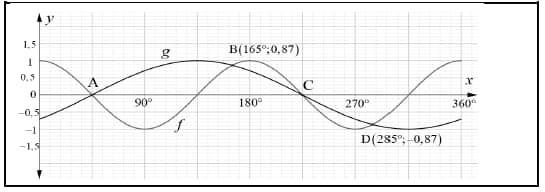
5.1 Write down the period of f. (1)
5.2 Write down the coordinates of A and C. (2)
5.3 For which values of x∈[0º;270] are g(x) strictly increasing? (2)
5.4 Which values of x are f (x) > g(x) ? (4)
5.5 Write down the range of 3.g(x). (2)
[11]

QUESTION 6
6.1 Complete the following statement:
The opposite angles of a cyclic quadrilateral … (1)
6.2 In the figure below, BAD is a diameter, BDG = 45º and ED = 8 cm.

Determine:
6.2.1 The size of BED (2)
6.2.2 The size of BDE (2)
6.2.3 The length of BE (2)
6.2.4 The length of GD (4)
6.3 In the figure below, ST || QW and JQK is a tangent to the circle. W₁ = 41º and Q₃ = 64º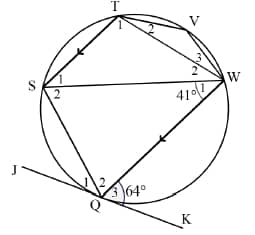

Determine the size of the following angles:
6.3.1 S₁ (2)
6.3.2 V (2)
6.3.3 S₂ (2)
[17]

QUESTION 7
7.1 Complete the following statement:
A line drawn parallel to one side of a triangle … (1)
7.2 The picture below is part of a roof truss. The diagram next to it, represent a part of the roof truss, where M is any point on side PQ of ΔPQR.
MN || PR with N on QR.
MC || PN with C on QR.
QM : MP = 3 : 2
CN = 2,86 cm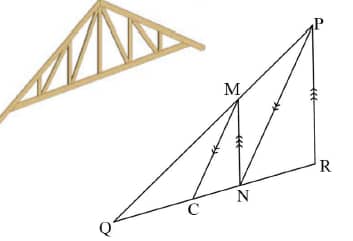

Calculate, correct to ONE decimal place:
7.2.1 The length of QC (5)
7.2.2 The length of NR (4)
7.3 In the diagram ΔABC is right-angled with 𝐴 = 90°. DE ⊥  BC, AC = 80 cm, BD = 100 cm and DE = 50 cm.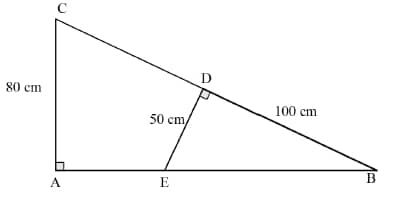

7.3.1 Prove that ΔBDE ||| ΔBAC. (3)
7.3.2 Determine, with reasons the length of AE. (4)
7.3.3 Determine:
Area ΔBDE
Area ΔBAC (3)
7.3.4 Determine the area of AEDC. (2)
[22]

QUESTION 8
8.1 Two circular pulleys with centres 80 cm apart are connected with a tight belt. The belt wraps ²/₃  of the way around the larger pulley, with centre A, which has a radius of 50 cm and ¹/₃ of the way around the smaller pulley, with centre B, which has a radius of 10 cm. The belt forms tangents to the pulleys.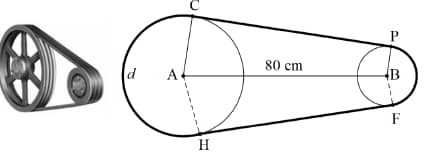

8.1.1 Show that the reflex CAH = 240º. (1)
8.1.2 Hence, calculate the size of CAB. (2)
8.1.3 Determine, d, the length of the belt from C to H, to the nearest integer. (5)
8.1.4 Determine the length of CP. (HINT: Draw BG || CP, with G on CA.) (5)
8.1.5 If it is given that the length of the belt, PF, is 21 cm, calculate the length of the whole belt. (2)
8.2 A chord of length 13 cm divides a circle of diameter 19 cm into two segments.
Calculate the height of the segments, to the nearest integer. (7)
[22]

QUESTION 9
9.1 A wheel rotates at 35 revolutions per second.
9.1.1 Calculate the angular velocity of the wheel. (3)
9.1.2 If the diameter of the wheel is 40 cm, calculate the circumference velocity in m/s. (4)
9.2 A cylinder is cast from a rectangular piece of alloy 5 cm by 7 cm by 12 cm. If the length of the cylinder is to be 60 cm, determine the diameter of the cylinder. (5)
[12]

QUESTION 10
The irregular figure below has one straight side divided into 5 equal parts 5 cm apart. The ordinates dividing the parts are 8 cm; 10 cm; 9 cm; 9 cm; 4 cm and 3 cm.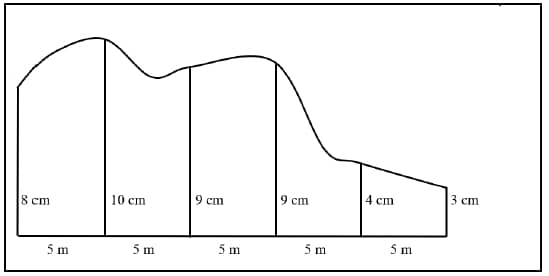
Calculate the area of the irregular figure. (4)
[4]
TOTAL: 150