GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - SENIOR CERTIFICATE EXAMINATIONS PAST PAPER (QUESTIONS) 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMathematics Paper 2
Grade 12
Senior Certificate Examinations
Past Paper (questions) 2016
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will not necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
On a certain day a tour operator sent 11 tour buses to 11 different destinations. The table below shows the number of passengers on each bus.
| 8 | 8 | 10 | 12 | 16 | 19 | 20 | 21 | 24 | 25 | 26 |
1.1 Calculate the mean number of passengers travelling in a tour bus. (2)
1.2 Write down the five-number summary of the data. (3)
1.3 Draw a box and whisker diagram for the data. Use the number line provided in the ANSWER BOOK. (2)
1.4 Refer to the box and whisker diagram and comment on the skewness of the data set. (1)
1.5 Calculate the standard deviation for this data set. (2)
1.6 A tour is regarded as popular if the number of passengers on a tour bus is one standard deviation above the mean. How many destinations were popular on this particular day? (2)
[12]
QUESTION 2
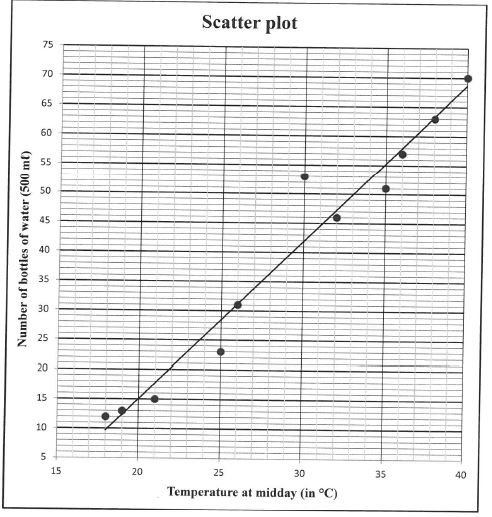
On the first school day of each month information is recorded about the temperature at midday (in °C) and the number of 500 ml bottles of water that were sold at the tuck shop of a certain school during the lunch break. The data is shown in the table below and represented on the scatter plot. The least squares regression line for this data is drawn on the scatter plot.
2.1 Identify an outlier in the data. (1)
2.2 Determine the equation of the least squares regression line. (3)
2.3 Estimate the number of 500 ml bottles of water that will be sold if the temperature is 28 °C at midday. (2)
2.4 Refer to the scatter plot. Would you say that the relation between the temperature at midday and the number of 500 ml bottles of water sold is weak or strong? Motivate your answer. (2)
2.5 Give a reason why the observed trend for this data cannot continue indefinitely. (1)
[9]
QUESTION 3
In the diagram below (not drawn to scale) A(-8; 6), B(8; 10), C and D(-2; 0) are the vertices of a trapezium having BC|| AD. T is the midpoint of DB. From B, the straight line drawn parallel to the y-axis cuts DC in F[ 8;31/3] and the x-axis in M.
3.1 Calculate the gradient of AD. (2)
3.2 Determine the equation of BC in the form y= mx + c. (3)
3.3 Prove that BDI AD. (3)
3.4 Calculate the size of BÔM. (2)
3.5 If it is given that TC ||DM and points T and C are symmetrical about line BM, calculate the coordinates of C. (3)
3.6 Calculate the area of ABDF. (5)
[18]
QUESTION 4
A circle having C(3 ;-1) as centre and a radius of 10 units is drawn. PTR is a tangent to this circle at T. R(k;21), C and P are the vertices of a triangle. TR = 20 units. 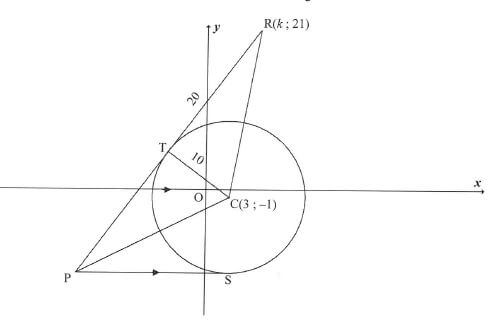
4.1 Give a reason why TC 1 TR.(1)
4.2 Calculate the length of RC. Leave your answer in surd form. (2)
4.3 Calculate the value of k if R lies in the first quadrant. (4)
4.4 Determine the equation of the circle having centre C and passing through T. Write your answer in the form (x -a)2 +(y- b)2 = r2 (2)
4.5 PS, a tangent to the circle at S, is parallel to the x-axis. Determine the equation of PS. (2)
4.6 The equation of PTR is 3y - 4x = 35
4.6.1 Calculate the coordinates of P.(2)
4.6.2 Calculate, giving a reason, the length of PT.(3)
4.7 Consider another circle with equation (x – 3)2 +(y+16)2 = 16 and having centre M.
4.7.1 Write down the coordinates of centre M. (1)
4.7.2 Write down the length of the radius of this circle. (1)
4.7.3 Prove that the circle with centre C and the circle with centre M do not intersect or touch. (3)
[21]
QUESTION 5
5.1 In the diagram PR ⊥ TS in obtuse triangle PTS.
PT = √5; TR = 2; PR = 1; PS = √10 and RS = 3 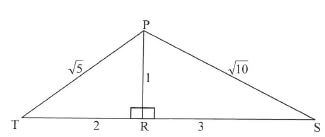
5.1.1 Write down the value of:
(a) sin Î (1)
(b) cos ŝ (1)
5.1.2 Calculate, WITHOUT using a calculator, the value of cos(Τ + S) (5)
5.2 Determine the value of:
1 - tan2 (180º + θ) (6)
COS(360º - θ).sin(90º - θ)
5.3 If sin x - cos x = 3/4, , calculate the value of sin 2x WITHOUT using a calculator. (5)
[18]
QUESTION 6
6.1 Determine the general solution of 4sin x + 2 cos2x = 2
6.2 The graph of g(x) = -cos 2x for x € [-180º ; 180º) is drawn below. 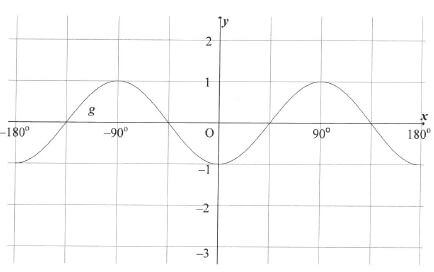
6.2.1 Draw the graph of f(x) = 2 sin x-1 for x€ [-180° ; 180°] on the set of axes provided in the ANSWER BOOK.(3)
6.2.2 Write down the values of x for which g is strictly decreasing in the interval x€[-180° ; 180°] (2)
6.2.3 Write down the value(s) of x for which f(x + 30°)- g (x + 30°) = 0 for x € [-180° ; 180°] (2)
[13]
QUESTION 7
From point A an observer spots two boats, B and C, at anchor. The angle of depression of boat B from A is 0. D is a point directly below A and is on the same horizontal plane as B and C. BD = 64 m, AB = 81 m and AC = 87 m.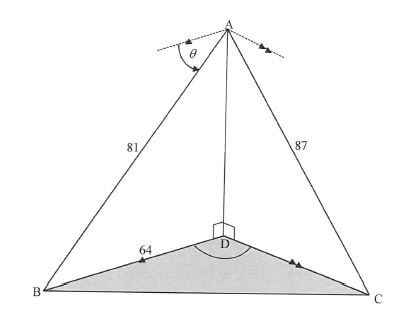
7.1 Calculate the size of θ to the nearest degree. (3)
7.2 If it is given that BÂC = 82,6º, calculate BC, the distance between the boats. (3)
7.3 If BỘC = 110º, calculate the size of DĈB. (3)
[9]
Give reasons for ALL statements in QUESTIONS 8, 9, 10 and 11.
QUESTION 8
8.1 In the diagram below, P, M, T and R are points on a circle having centre 0. PR produced meets MS at S. Radii OM and OR and the chords MT and TR are drawn. Τ1= 148°, PMO=18° and Ŝ= 43°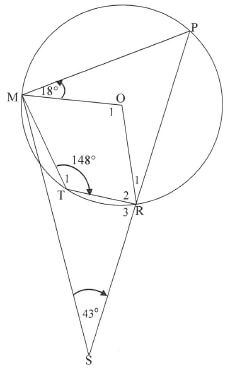
Calculate, with reasons, the size of:
8.1.1 P (2)
8.1.2 O1 (2)
8.1.3 OMS (2)
8.1.4 R3, if it is given that TMS= 6° (2)
8.2 In the diagram below, the circle passes through A, B and E. ABCD is a parallelogram. BC is a tangent to the circle at B. AE = AB. Let Ĉ1 = x 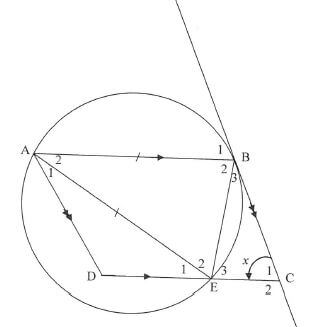
8.2.1 Give a reason why B1 = x (1)
8.2.2 Name, with reasons, THREE other angles equal in size to x. (6)
8.2.3 Prove that ABED is a cyclic quadrilateral. (3)
[18]
QUESTION 9
9.1 Complete the statement so that it is TRUE:
The angle between the tangent to a circle and the chord drawn from the point of contact is equal to the angle ... (1)
9.2 In the diagram below, two unequal circles intersect at A and B. AB is produced to C such that CD is a tangent to the circle ABD at D. F and G are points on the smaller circle such that CGF and DBF are straight lines. AD and AG are drawn.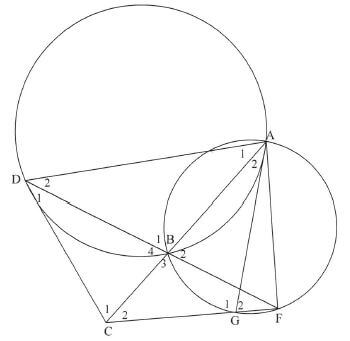
Prove that:
9.2.1 B4 =D1 +D2 (4)
9.2.2 AGCD is a cyclic quadrilateral (4)
9.2.3 DC = CF (4)
[13]
QUESTION 10
10.1 In the diagram below, ΔMVT and ΔAKF are drawn such that M =Â, V =K and T = F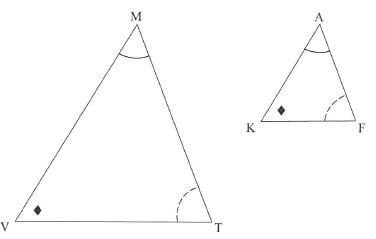
Use the diagram in the ANSWER BOOK to prove the theorem which states that if two triangles are equiangular, then the corresponding sides are in proportion,
that is: MV = MT
AK AF
10.2 In the diagram below, cyclic quadrilateral EFGH is drawn. Chord EH produced and chord FG produced meet at K. M is a point on EF such that MG || EK. Also KG = EF 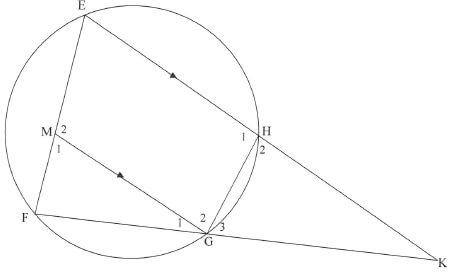
10.2.1 Prove that:
(a) ΔKGH ||| ΔKEF (4)
(b) EF2 = KE .GH (2)
(c) KG2 = EM . KF (3)
10.2.2 If it is given that KE = 20 units, KF = 16 units and GH = 4 units, calculate the length of EM. (3)
[19]
TOTAL: 150
INFORMATION SHEET