GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - SENIOR CERTIFICATE EXAMINATIONS PAST PAPER (MEMORANDUM) 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMathematics Paper 2
Grade 12
Senior Certificate Examinations
Past Paper (memorandum) 2016
NOTE:
- If a candidate answered a question TWICE, mark only the FIRST attempt.
- If a candidate has crossed out an attempt to answer a question and did not redo it, mark the crossed-out version.
- Consistent accuracy applies in ALL aspects of the marking memorandum. Stop marking at the second calculation error
- Assuming answers/values in order to solve a problem is NOT acceptable.
MEMORANDUM
QUESTION 1
| 8 | 8 | 10 | 12 | 16 | 19 | 20 | 21 | 24 | 25 | 26 |
| 1.1 | Mean = 189/11
| ✓189 | |
| 1.2 | Min = 8, max = 26 | ✓ min, max | |
| 1.3 |  | ✓ box | |
| 1.4 | The data is skewed to the left OR Negatively skewed | ✓ answer (1) | |
| 1.5 | SD/SA = 6,46 | ✓✓ answer (2) | |
| 1.6 | 17,18 + 6,46 = 23,64 | ✓ interval |
QUESTION 2
| Temperature at midday (in °C) | 18 | 21 | 19 | 26 | 32 | 35 | 36 | 40 | 38 | 30 | 25 |
| Number of bottles of water (500 mℓ) | 12 | 15 | 13 | 31 | 46 | 51 | 57 | 70 | 63 | 53 | 23 |
| 2.1 | (30 ; 53) | ✓answer (1) |
| 2.2 | a = – 38,51 b = 2,68 ∴ yˆ = 2,68x – 38,51 | ✓ value a ✓ value b ✓ equation (3) |
| 2.3 | ∴ yˆ ≈ 36,53 bottles OR | ✓✓ answer (2) ✓substitution |
| 2.4 | Strong The majority of the points lie close to the regression line. OR Strong | ✓ strong ✓strong/sterk |
| 2.5 | Temperature cannot rise beyond a certain point as this would be life threatening OR there is only so much water one can consume before it becomes a risk to your health (hyponatremia)./ | ✓ reason(1) [9] |
QUESTION 3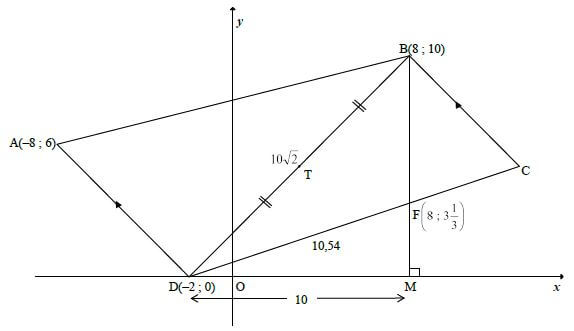
| 3.1 | mAD = y2 - y1 x2 - x1 = 0 - 6 -2 +8 = -6 = -1 6 | ✓substitution ✓–1 (2) |
| 3.2 | mBC = -1 [BC | | AD] mBC = -1 [BC | | AD] | ✓ gradient ✓substitute m and (8 ; 10) ✓ equation (3) |
| 3.3 | mBD = y2 - y1 OR AD2 = 72 or AD = √72 or 6√2 | ✓substitution ✓ answer ✓ ⋅ mBD × mAD = 1 × -1 = -1 (3) ✓✓ calculating all 3 sides ✓ AB2 = AD2 + BD2 (3) |
| 3.4 | tan BDM = MBD = 1
| ✓ tan BDM = MBD ✓sin BDM = 1 |
| 3.5 | T (x ; y) =[ x1 + x2 ; y1 + y2] OR mDF = 31/3 - 0 = 1 | ✓T(3 ; 5) ✓eq of DF ✓value of x ✓ value of y (3) |
| 3.6 | area ΔBDF = area ΔBDM - area ΔDFM OR area ΔBDF = ½. BF.DM OR tan FDM =mDC = 5 - 0 = 1 or tan FDM = FM = 10/3 = 1 OR BF = 20/3 or 62/3 OR area Δ BDF OR tan FDM =mDC = 5 - 0 = 1 or tan FDM = FM = 10/3 = 1 | ✓ formula/method ✓ formula/method ✓ gradient/ratio
✓ BF ✓ formula/method ✓ gradient/ratio |
QUESTION 4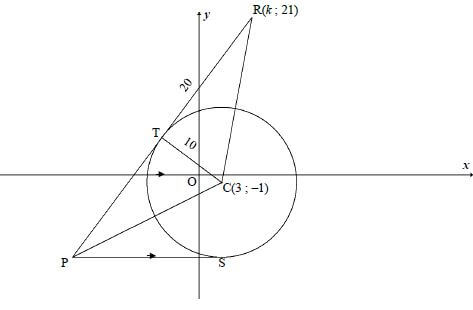
| 4.1 | radius ⊥ tangent | ✓ R (1) |
| 4.2 | CR² = TR² + CT² (Pyth) | ✓ substitution ✓ answer (2) |
| 4.3 | CR² = (X2 - X1)² + (Y2 -Y1)² OR CR² = (X2 - X1)² + (Y2 -Y1)² | ✓ substitution
|
| 4.4 | (x - 3)² + (y + 1)² = 100 | ✓✓ answer (2) |
| 4.5 | CS = 10 and CS ⊥ PS ∴S(3; −11) | ✓S(3; −11) |
| 4.6.1 | S(3;-11) OR 4/3x + 35/3 = -11 | ✓ substituting ✓ answer (2) ✓ equating
|
| 4.6.1 | PT = PS [tangents from common point] OR
OR
| ✓ S ✓R ✓ value of PC ✓ value of PC |
| 4.7.1 | M(3;−16) | ✓answer (1) |
| 4.7.2 | Radius = 4 | ✓ answer (1) |
| 4.7.3 | r1 + r2 = 10 +4 = 14 distance CM = = √225 = 15 CM > r1 + r2 Therefore the two circles do not intersect or touch | ✓r1 + r2 ✓ 15 |
QUESTION 5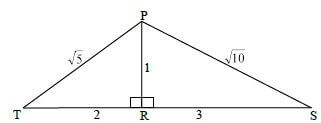
| 5.1.1(a) | sin T = 1/√5 = √5/5 = 0,45 | ✓value (1) |
| 5.1.1(b) | cos S = 3/√10 = 3√10/10 = 0,95 | ✓value (1) |
| 5.1.2 | cos (T + S) = cosTcosS - sinTsinS = 6/√50 - 1/√50 = 5/√50 or 1/√2 or √2/2 | ✓expansion ✓ simplification |
| 5.2 | 1 - tan2(180º + θ) cos(360º - θ)sin(90º - θ) = 1 - tan2 θ (cos θ)(cos θ) = 1 - (sin2 θ) (cos2 θ) (cos2 θ) = 1 - sin2 θ cos2 θ = cos2 θ or 1 - sin2 θ cos2 θ 1 - sin2 θ | ✓cosθ ✓tan2 θ ✓sin2 θ ✓ answer (6) |
| 5.3 | (sin x - cos x)2 = [3/4]2 sin²x - 2sinxcosx + cos²x = 9/16 1 - 2sinxcosx = 9/16 2sinxcosx = 7/16 ∴sin2x = 7/16 | ✓ squaring both sides |
QUESTION 6
| 6.1 | 4sinx + 2 cos 2x = 2 2sinx + cos 2x - 1 = 0 | ✓using identity ✓ k.180° |
| 6.2.1 | 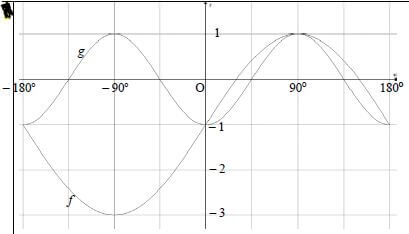 | ✓ turning point (–90° ; –3) |
| 6.2.2 | (−90°;0°) | ✓ ✓ answer (2) ✓ ✓ answer (2) |
| 6.2.3 | f(x) = g(x) ∴ -180º ; 0º; 90º; 180º f(x +30º) = g(x + 30º) ∴x = -30º; 60º ; 150º | ✓ any ONE correct ✓ other 2 correct (2) [13] |
QUESTION 7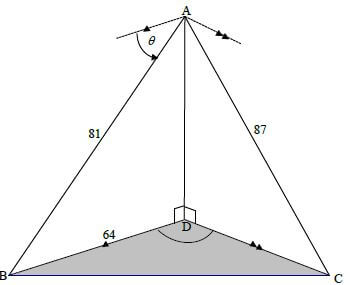
| 7.1 | ABD = θ [alternate∠s ; || lines] OR | ✓correct trig ratio
✓correct trig ratio |
| 7.2 | BC² = AB² + AC² - 2(AB)(AC)cosBAC =81² + 87² - 2(81)(87)cos82,6º =12312,754..... BC = 110,97m | ✓use cosine rule ✓correct substitution into cosine rule ✓answer (3) |
| 7.3 | sinDCB = sinBDC BD BC sinDCB = BD.sinBDC BC sinDCB = 64.sin110º 110,97 ∴DCB = 32,82º | ✓ use sine rule |
QUESTION 8
8.1 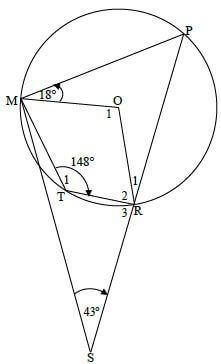
| 8.1.1 | P = 32º [opp ∠ s of cyclic quad | ✓ S |
| 8.1.2 | O1 = 2(32º) = 64º [∠centre = 2∠ at circum ] OR reflex O = 296º [∠centre = 2∠ at circum] | ✓ S ✓R (2) ✓ S and R |
| 8.1.3 | OMS = 180º -(32º +18º +43º) [sum ∠ sΔ] = 87º | ✓ S ✓ S (2) |
| 8.1.4 | R3 = TMP = 87º + 18º - 6º =99º | ✓ R ✓ S (2) |
8.2 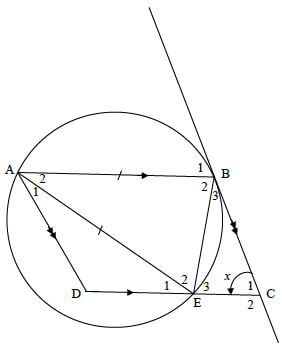
| 8.2.1 | corres ∠s; AB| | DC | ✓ R (1) |
| 8.2.2 | E2 = x [tan - chord theorem] Any 3 ∠s correct | ✓S ✓R ✓ S ✓ R ✓ S ✓ R (6 |
| 8.2.3 | D = 180º - x [co - int ∠s suppl ; AD || BC] OR DAB = x [OPP ∠s ||m] OR [alt ∠s ; BC|| AD] | ✓S ✓ R ✓S ✓ R |
QUESTION 9
| 9.1 | … in the alternate segment | ✓ answer (1) |
9.2 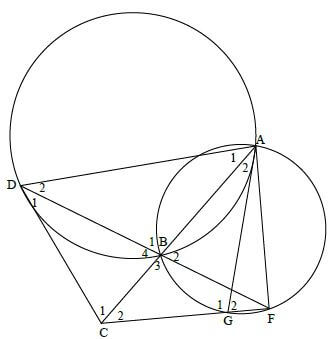
| 9.2.1 | A1 = D1 [tan chord theorem] B4 = A1 + D2 [ext ∠ Δ] =D1 + D2 | ✓S ✓ R ✓ S ✓ R (4) |
| 9.2.2 | B4 = B2 [vert opp ∠s] D1 + D2 = B2 [proven] =G2 [∠s in same segment] ∴ AGCD is cyc quad [converse ext ∠ cyc quad] | ✓ S ✓ S ✓ R ✓ R (4) |
| 9.2.3 | D1 = A2 [∠s in same segment] A2 = F [∠s in same segment] ∴ D1 = F ∴ DC = CF [side opp ∠s ] | ✓ S ✓ R ✓ S ✓ R (4) [13] |
QUESTION 10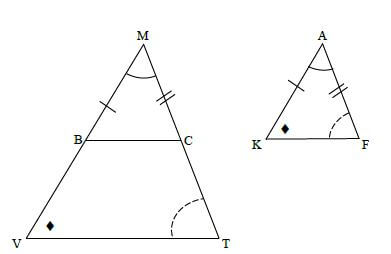
| 10.1 | Constr: Draw line BC such that MB = AK and MC = AF Proof: In ΔBMC and ΔKAF MB = AK [constr] M = A [given] MC = AF [constr] ΔBMC = ΔKAF [s∠s] ∴MBC = AKF or MCB = AFK [ΞΔ] but V = K or T = F [given] ∴MBC = V or MCB = T But these are corresponding ∠s ∴ BC || VT [corr∠s≡] ∴ MV = MT [prop theorem; BC || VT] MB MC but MB = AK and MC = AF [const] ∴ MV = MT AK AF | ✓ constr/konstr ✓ S / R
✓ S / R ✓S ✓R (7) |
10.2
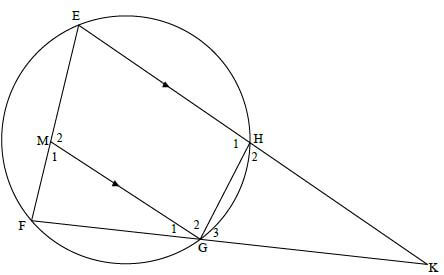
| 10.2.1 (a) | In ΔKGH and ΔKEF K is common H2 = F [ext ∠ CYCLIC QUAD] G3 = E [sum∠s Δ or ext∠cyclic quad] ∴ ΔKGH ||| ΔKEF [∠∠∠] | ✓ S ✓S ✓R ✓ naming third angle OR ∠∠∠ (4) |
| 10.2.1 (b) | EF = KE [||| Δs] GH KG ∴ EF = KE GH EF [KG = EF] ∴ EF2 = KE.GH | ✓ S ✓ S (2) |
| 10.2.1 (c) | KG = EM [prop theorem ; MG || EK] KF EF but EF = KG [given] KG = EM KF KG KG2 = EM.KF | ✓ S ✓ R ✓ S (3) |
| 10.2.2 | KE.GH = EM.KF EM = 20 × 4 16 =5 units | ✓ KE.GH = EM.KF ✓ substitution ✓ answer (3) [19] |
TOTAL: 150