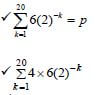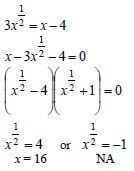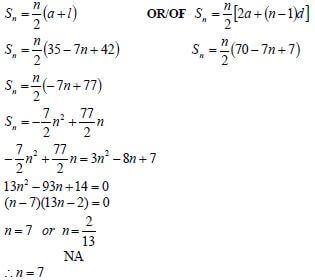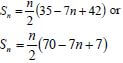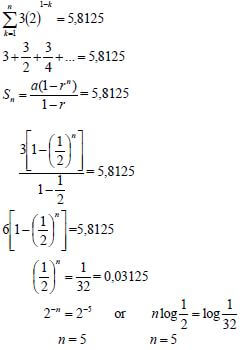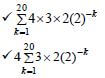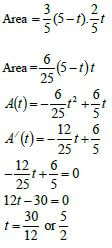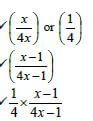MATHEMATICS
MEMORANDUM NOTE:
If a candidate answers a question TWICE, only mark the FIRST attempt. Consistent Accuracy applies in all aspects of the marking memorandum. QUESTION 1
1.1.1
x2 − 4x + 3 = 0
✔factors/correct subt in formula
1.1.2
✔substitution into the correct formula
1.1.3
x2 − 3x − 10 > 0
OR
✔factors/ critical values
1.1.4
3√x = x − 4 2 − 8x + 162 − 17x + 16 = 0
✔ squaring both sides
OR
OR
1.2
2y + 9x2 = -1......(1) 2 = -12 = -12 + 6x - 3 = 0 2 + 2x - 1 = 01 /3 or x = -1
OR
2y + 9x2 = -1 ....... (1)y + 2 y + 2 )2 = -1y2 + 4y + 4) = -12 + 4y + 4 + 1 = 01 /3 or x = -1
✔y = 3x − 2
OR
✔x = y + 2
1.3
✔33x = 43x - 3 or 33x .3-1
OR
✔33x - 3 or 33x .3-1 3x = 4
[23]
QUESTION 2
2.1.1
42
✔answer (1)
2.1.2
2a = 6 3a + b = 1 a + b + c = 2 n = 3n2 + 8n + 7
OR
2a = 6 n = 3n2 + bn + c1 : 3 + b + c = 2 b + c = -1 ....(1)2 : 12 + 2b + c = 3 2b + c = -9 ....(2)2 - T1 : b = -8
Subst. in (1): – 8 + c = – 1 n = 3n2 + 8n + 7
✔ a = 3 n = an2 + bn + c (4)
OR
✔ a = 3 n = an2 + bn + c (4)
2.1.3
T20 = 3(20)2 - 8(20) + 7
✔substitution
2.2
Tn = −7n + 42
✔Tn = −7n + 42
2.3
✔n
[16]
QUESTION 3
3.1
r = ½ and = S∞ = 6 ∞ = a a
✔substitution
3.2
Tn = arn-1 8 = 3(1 /2 )78 = 3
✔✔ T8 = 3(1 /2 )7 (2)
3.3
✔ r = 1 /2
3.4 ✔expansion
OR
OR
OR
✔ substitution and answer
[11]
QUESTION 4
4.1
Yes
✔answer
4.2
R(–12 ; –6)
✔answer (1)
4.3
f (x) = ax2 substitute (-6 ; -12) 2 a = −1 /3
✔substitution
4.4
f : y = −(1 /3 ) x2 1 /3 ) y2 2 = -3x
✔swapping x and y 2 = -3x
[8]
QUESTION 5
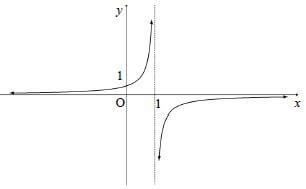
5.1
Domain: x∈R ; x ≠1
OR
x∈(−∞;1)∪(1;∞)
✔answer (1)
5.2
x = 1
✔x = 1
5.3
✔ y intercept
5.4
x ≥ 0 ; x ≠1
OR
0 ≤x < 1 or x > 1
OR
x∈[0;1) ∪(1;∞)
✔x ≥0
OR
✔ 0 ≤ x < 1
[8]
QUESTION 6
6.1
y = mx + c
OR
y = mx + c
✔substitution into gradient formula
OR
✔substitute (4 ; 5)
6.2
x2 − 2x − 3 = 0
✔y = 0
6.3
x = −1 + 3 or x = -b = -(-2) or fI (x) = 2x - 2 = 0 2 - 2x - 3 2 - 2(1) - 3 or y = (x2 - 2x + (-1)2 ) - 3 - 1 2 - 4
✔x -value
6.4.1
MN: y = (x2 - 2x - 3) - (x + 1)2 - 3x - 42 - 3x - 42 - 3x - 10
✔ x2 - 3x - 4
6.4.2
y = x +1 substitute x = −2
✔substituting x = –2
6.5
OR
x2 − 2x − 3 = x + p 2 − 2x − 3 − x − p = 02 − 4ac = 02 - 4(1)(-3 - P) = 0 -21 21
✔f ′(x) = 2x − 23 /2 ✔
OR
✔equating
6.6
k < - 21
✔answer (1)
[20]
QUESTION 7
7.1.1
✔0,088 and n = 16
7.1.2
✔ future value – amount including interest
OR
✔ R15 000 including interest – R100 000 V
7.2.1
✔i = 0,105
7.2.2
= R5 259 229,61– R4 289 302,47
✔R14 975,70 in Pv -formula
OR
✔ n = 144 in A-formula v -formula
[15]
QUESTION 8
8.1
✔x2 + 2xh + h2 − 5
OR
✔x2 + 2xh + h2 − 5
8.2.1
y = 3x3 + 6x2 + x − 4dy = 9x2 + 12x + 1
✔9x2 ✔12x
8.2.2
y(x −1) = 2x(x −1) 2x(x - 1) if x # 1dy = 2
✔y(x −1)
[12]
QUESTION 9
9.1.1
g(x) = (x + 5)(x − x1 )2 20 = 5(x1 )2 x1 2 = 4 1 2 = 2 2 g(x) = (x + 5)( x2 − 4x + 4)3 + x2 − 16x + 20
✔(x +5) 1 = 2 2 − 4x + 4) (4)
9.1.2
g(x) = x3 + x2 − 16x + 202 + 2x − 16-8 or x = 2-8 ; 1372 ) or R(-2,67;50,81)
✔derivative
9.1.3
g′′(x) = 6x + 2
OR
g′′(x) = 6x + 2 1 /3 is the point of inflection
✔g′′(x) = 6x + 2
OR
✔g′′(x) = 6x + 2 1 /3 ✔conclusion (3)
9.2
✔ y – intercept of a cubic graph
[15]
QUESTION 10
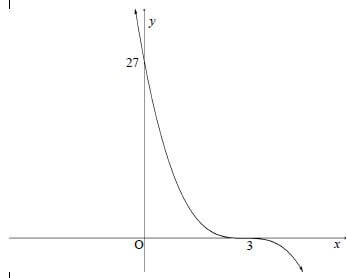
10.1
AH = 3
✔ answer (1)
10.2
Area of a parallelogram = base× ⊥height
✔ 2 /5 t3 /5 (5 − t) 6 /25 t2 + 6 /5 t12 /25 t + 6 /5 ✔answer (5)
[6]
QUESTION 11
11.1.1
75 = 16 807
✔✔ answer (2)
11.1.2
7 × 6 × 5 × 4 × 3 7! = 2520
✔7 × 6 × 5 × 4 × 3 or 7!
11.2
2×7×1= 14
✔✔✔2 × 7 × 1 (3)
[7]
QUESTION 12
12.1
P(A or B) = P(A) + P(B)
✔ P(A or B) = P(A) + P(B)
12.2
✔ 4x 7
OR 7 = 1 × P(gift at second draw) 7 ÷ 1 14 15 /60 And: 15 bags had mystery gifts inside
OR
✔¼ 1 × P(gift at 2nd draw) 7 ÷ 1 P(gift at 2nd draw) 14 15 /60 ✔answer (6)
[9]
TOTAL: 150