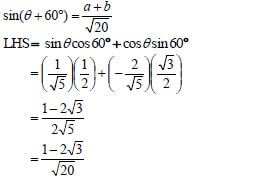GEOMETRY

S

A mark for a correct statement
(A statement mark is independent of a reason)

R

A mark for the correct reason
(A reason mark may only be awarded if the statement is correct)

S/R

Award a mark if statement AND reason are both correct

1.1.1

140 items

✓ answer(1)

1.1.2

Modal class: 20 <  x ≤ 30 minutes
OR
20 ≤ x <  30 minutes

✓ answer(1)
✓ answer (1)

1.1.3

Number of minutes taken = 20 minutes

✓answer (1)

1.1.4

140 - 126 [Accept:  124 to 128]
14 orders (12 to 16)

• Answer only: Full marks

✓126
✓ answer (2)

1.1.5

75^th percentile is at 105 items
=37 minutes [accept 36 - 38 minutes]

• Answer only: Full marks

✓105
✓ answer (2)

1.1.6

Lower quartile is at 35 items
Answer only: Full marks
=21,5 min [accept 21 - 23 min]
IQR = 37 - 21,5 
= 15,5 min [accept 13 - 17 min]

✓ lower quartile (Q1)
✓ answer (2)

35

70

75

80

80

90

100

100

105

105

110

110

115

120

125

1.2.1(b)

σ = R22,691...=  R22,69

✓✓ answer (2)

1.2.2(a)

They both collected the same (equal) amount in tips, i.e. R1 420 over the 15-day period.

✓ answer (1)

1.2.2(b)

Mary's standard deviation is smaller than Reggie's which suggests that there was greater variation in the amount of tips that Reggie collected each day compared to the number of tips that Mary collected each day.

✓ explanation (1)

[15]

2.1

251 km/h

✓ answer (1)

2.2.1

r = 0,52   OR   C

✓ answer (1)

2.2.2

The points are fairly scattered and the least squares regression line is increasing.

✓ reason (1)

2.3

There is a weak positive relation hence the height could have an influence
OR
There is no conclusive evidence that the height of a player will influence his/her tennis serve speed. 
OR
There is no conclusive evidence that a taller person will serve faster than a shorter person.

✓ answer (1)
✓  answer (1)
✓ answer (1)

2.4

For (0 ; 27,07), it means that the player has a height of 0 m but can serve at a speed of 27,07 km/h.
It is impossible for a person to have a height of 0 m.
OR
This means that the player does not exist and therefore cannot serve and have a serve speed.

✓ explanation (1)
✓ explanation (1)

[5]

3.1.1

m_KN = y₂ -  y₁
           x₂ - x₁
m_KN =  2 - (-1)
             -1 - 1
= = -3
        2

• Answer only: Full marks

✓ correct substitution
✓  answer (2)

3.1.2

tan θ = m_KN = -3
                         2
θ = 180º - 56,31º
θ = 123,69º

• Answer only: Full marks

✓ tan θ = m_KN = -3
                            2
✓ answer (2)

3.2

Inclination KL = 123,69º - 78,69º =  45º  [ext ∠Δ]
tan45º m_KL = 1

✓ S
✓ tan 45º = m_KL = 1 (2)

3.3

y = x + c
2 = -1 + c
c = 3
y = x + 3

OR

y - y₁ = 1(x - x₁)
y -2 = 1(x - (-1))
y = x + 3

✓ substitute (- 1 ; 2) and m
✓ equation (2)
✓ substitute (- 1 ; 2) and m
✓ equation (2)

3.4

KN = √13  or 3,61         

• Answer only: Full marks

✓ substitute K and N into distance formula
✓ answer (2)

3.5.1

(x + 3)² +  (y + 5)² = 13               ...(1)
L is a point on KL
y = x + 3                               …(2)
(2) in (1):
(x + 3)² + (x + 3 + 5)  = 13
x² + 6x +  9 + x² + 16x +  64 = 13
2x² +  22x +  60  = 0
x² + 11x + 30 = 0
(x +  5)(x + 6) = 0
x = -5 or x = -6
y = -2 or y = -3
L(-5 ; -2) or (-6 ; -3)

OR

(x+ 3)² +  (y + 5) = 13               ...(1)
L is a point on KL
y = x + 3      ∴ x = y - 3        …(2)
(2) in (1):
(y - 3 + 3)² + (y + 5)² = 13
y² +  y² + 10y +  25 = 13
2y² + 10y + 12 =  0
y² + 5y +  6  = 0
(y + 2)(y = 3) = 0
y = -2 or y = -3
x = -5 or x = -6
L(-5 ; -2) or (-6 ; -3)

✓  equation (1)
✓ substituting eq (2)
✓  standard form
✓  x-values
✓  y-values (5)

✓ equation (1)
✓  substituting eq (2)
✓  standard form
✓  y-values (both)
✓  x-values (both) (5)

3.5.2

✓  midpoint of KM
✓  x value ✓  y value (3)
✓   m_LM = m _KN
✓  x value
✓  y value (3)

3.6

✓ coordinates of T
✓ length of KT
✓ substitution into area rule
✓ answer (4)

✓ length of TL
✓ length of KT
✓ substitution into area rule
✓ answer (4)

[22]

4.1

F(3 ;1)

✓ x value ✓ y value (2)

4.2

FS = √ (6 - 3)² +  (5 - 1)²
FS = 5

✓ substitution  of   F & S
✓  answer (2)

4.3

FH(FS) : HG = 1 : 2
∴HG = 2 FH
= 10

✓ HG = 10 (1)

4.4

Tangents from common/same point

✓ answer (1)

4.5.1

FHJ =  90º                                      [tan ⊥ radius ]
FJ² = 20² + 5²                                 [Pyth theorem]
FJ = √425 or 5√17 or 20,62

✓ S ✓ R
✓ S
✓ answer (4)

4.5.2

(x - m)² +  (y - n)² = 100

✓ answer  (1)

4.5.3

K(22; n)                                   [radius ⊥ tangent]
GK = HG = 10                                   [radii]
FH = FS = 5                                       [radii]
m = 22 - 10
m = 12
F, H and G are collinear             [HJ is a common tangent]
FG² = (12 -  3)² +  (n - 1)²
15² =  81 + (n - 1)²
(n - 1)² = 144                                                n² - 2n - 143 = 0
n- 1 = ±12                       OR                       (n + 11)(n - 13) = 0
n # 13 or  n = -11                                      n = -11  or n # 13
∴G(12; -11)

OR

K(22; n)                                   [radius  ⊥ tangent]
GK = HG = 10                                   [radii]
FH = FS = 5                                       [radii]
m = 22 - 10
m = 12
Let J(22 ; y):
FJ² =  (22 - 3)²  + (y - 1)²
425 = 361+ y² -  2y + 1
0 =  y² - 2y - 63
0 =  (y - 9)(y + 7)
∴ y = 9 or  y # -7
∴ n = 9 - 20 = -11
∴G(12; -11)

✓ K(22; n)
✓ value of m
✓ subst. of F and G in distance formula
✓ FG = 15
✓ simplification/ standard form
✓  value of n
✓ coordinates of G (7)

✓ K(22; n)
✓ value of m
✓ subst. of F and J in
✓istance formula
✓ FJ =  √425
✓ standard form
✓ value of n
✓ coordinates of G (7)

[18]

5.1.1

k²  = ( √5)² - 1²
= 4
k = -2

• Answer only: full marks

✓ substitution into theorem of Pythagoras
✓ answer (2)

5.1.2(a)

tanθ = -½

✓ answer (1)

5.1.2(b)

cos(180º + θ ) = - cosθ
= 2
 √5
Answer only: full marks

✓  reduction
✓  answer (2)

5.1.2(c)

✓  expansion
✓ subst of sin θ
✓  subst of cos θ
✓ both special ∠s
✓ 1 - 2 √3    (5)
       2 √5

5.1.3

tanθ = -½
∴ θ = 180º - 26,57º
∴ θ = 153,43º
tan(2θ - 40º) = tan[(2 × 153,43º) - 40º]
=  tan266,87º
=18,3

✓ θ
✓ substitution
✓ answer (3)

5.2

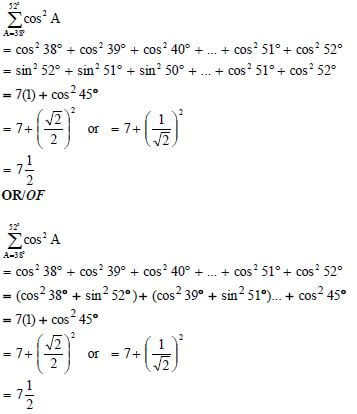✓ single fraction
✓ expansion
✓ simplification (both)
✓ double ∠  identity
✓ double ∠  identity (5)

✓ single fraction
✓ difference of two squares
✓ simplification (both)
✓ double ∠   identity
✓ double ∠   identity (5)

✓ double ∠   identity
✓  double ∠   identity
✓  identity & method
✓  factorising numerator and denominator
✓  writing as 2 terms (5)

✓ expansion
✓  co ratio
✓  cos²45º
✓ 7 × identity
✓ answer (5)

✓ expansion
✓ pairing
✓ cos²45º
✓ 7 × identity
✓ answer

6.1

Period = 120°

✓ answer  (1)

6.2

2 = -2tan ³/₂ x
tan (³/₂ t) = -1 
³/₂ t = 135º + k.180º       OR   ³/₂ t = -45º + k.180º
t = 90º + k.120º ; k∈Z              t = -30º + k.120º ; k∈Z

OR

2 = -2 tan ³/₂ x
tan (³/₂ t) = -1
³/₂ t = 135º + k.360º   or    ³/₂ t = 315º + k.360º
t = 90º + k.240º 0r t = 210 + k.240º ;  k∈Z

✓ equating
✓  general solution of ³/₂ t
✓  general solution of t  (3)
✓ equating
✓ general solution of  ³/₂ t
✓  general solution of t  (3)

6.3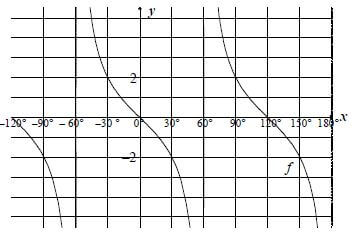

✓ asymptotes: x = ± 60°;  x = 180°
✓ x-intercepts 0°; ±120°
✓ negative shape
✓ (90° ; 2) or (-30° ; 2) or (30° ; -2) or (-90° ; -2)  (4)

6.4

x∈ (-60º ; -30º] or (60º;90º]

OR

–60°< x ≤  -30°  or 60° < x ≤  90°

✓ interval  ✓ interval
✓ notation (3)

✓ interval  ✓ interval
✓ notation (3)

6.5

Translation of 40° to the left / skuif met 40° links

✓ Translation of 40°
✓  to the left  (2)

[13]

7.1

ABD = 30
sin 30º = h  
              AB
AB =  h     OR   AB =   h   OR   AB = 2h
       sin 30º                ½

OR 

BAD = 60º
cos60º =  h   
               AB
AB =  h     OR    AB =   h     OR   AB = 2h  
      cos 60º                   ½

✓ A BD = 30º
✓  answer (2)

✓ BAD = 60º
✓ answer (2)

7.2

BC² = AB² + AC - 2AB.ACcosBÂC
= (2h)² + (3h)² - 2(2h)(3h) cos 2x
= 13h² - 12h² (2cos² x - 1)
= 13h² - 24h²cos²x +12h²
=  25h² - 24h²cos²x
BC = h √25  - 24 cos²x

✓ use of cosine rule in  ΔABC
✓ substitution
✓ double angle identity
✓ 25h² - 24h²cos² x² (4)

[6]

8.1.1

P = M₁ =  66º                             [tan chord theorem]

✓S  ✓R  (2)

8.1.2

M₂ =  90º                                   [∠ in semi circle]

✓S  ✓R   (2)

8.1.3

N₁ = 180º  -  (90º + 66º) = 24º               [sum of ∠s of  ∠èΔMNP]

✓S  (1)

8.1.4

Ô₂   =  P  =  66º                [corres. ∠s; ∠e, PM || OR]

✓S  ✓R  (2)

8.1.5

R + N₁ + N₂ = 180º - 66º   = 114º             [sum of ∠s of ∠e ΔRNO]
R + N₁ + N₂ = 57º                   [∠s opposite = radii/∠e]
∴N₂ = 33º

OR

POR = = 114º                       [∠s on straight line]
PNR = 57º                        [∠ at centre = twice ∠ at circumference]
∴N₂ = 33º

✓S
✓S/R
✓ S  (3)

✓S
✓ S/R
✓S  (3)

8.2.1

FC || AB || GH           [opp sides of rectangle]

✓ R  (1)

8.2.2

AC  =    AF  [line || one side of Δ]  OR  [prop theorem; FC || GH]
CH       FG
AC = 20
21     15
AC = 20 × 21
             15
= 28
DB = AC = 28       [diags of rectangle  = ]
DM = ½DB = 14   [diags of rectangle bisect]

✓S  ✓R
✓ AC
✓ S
✓ S  (5)

[16]

9.1

Constr  Draw KO and MO
Proof:
Ô₁ = 2Ĵ                           [∠ at centre = twice ∠ at circumference]
Ô₂ = 2L                          [∠ at centre = twice ∠ at circumference]
Ô₁ + O₂ = 360º             [∠s around a point ]
∴2Ĵ + 2L =  360º
∴2(Ĵ + L) =  360º
∴Ĵ + L =  180º

OR

Constr  Draw KO and MO
Proof:
Let  Ĵ = x
Ô₁ = 2x                        [∠ at centre = twice ∠ at circumference]
O₂ = 360º  - 2x             [∠s around a point ]
∴L =  180º - x               [at centre = twice ∠ at circumference]
∴Ĵ + L =  180º

✓ construction
✓ S/R
✓ S
✓ S/R
✓ S(5)

✓ construction
✓ S ✓ R
✓ S/R
✓ S (5)

9.2.1(a)

B₁ =  x                            [∠s in same seg]

✓ S  ✓ R  (2)

9.2.1(b)

B₂ = y                            [ext ∠ of cyclic quad]

✓ S  ✓ R  (2)

9.2.2

C = 180º - (x + y)             [sum of  ∠e, Δ ACR]
SBD + C = X + Y + 180º - (x + y)
SBD + C =  180º
SCDB is a cyclic quad [converse opp angles of cyclic quad]

OR

S₁ = T₂                    [∠s in same segment]
T₂ = DQ + D₂ = BDR     [ext ∠ of cyc quad]
∴ S₁ = BDR
∴ SCDB is cyc quad      [ext ∠ of quad = opp ∠]

✓ S
✓ S
✓ R (3)

✓ S
✓ S
✓ R (3)

9.2.3

T4 = y - 30º                             [ext ∠ of TDR]
T1 = y - 30º                           [vert opp ∠s  =]
y = 30º + x + 100º = 180º             [sum of ∠s of AST]
∴x + y = 110º
SBD = 110º
∴ SD not diameter         [line does not subtend 90° ∠]

OR

AST = C + D₂                [ext ∠ of  SCD]
C = 100º - 30º = 70º
SBD = 180º - 70º        [opp ∠s cyclic quad]
=  110º
∴ SD not diameter         [line does not subtend 90° ∠]

✓ S
✓ S
✓ S
✓ R  (4)
✓ S
✓ S
✓ S
✓ R  (4)

[16]

10.1.1

A₂ = A₁ = 90º  - x                 [= chords subtend = ∠s]
D₂ = x                                   [exterior angle of cyclic quad∠]
∴C₂ = 90º - x                          [sum of ∠s of  ∆DCM]
∴C₂ = A₁ = 90º - x 
∴MC is a tangent to the circle at C [converse: tan chord th]

OR

A₂ = A₁ = 90º  - x                 [= chords subtend = ∠s]
C₁ + C₂ = x                          [sum of ∠s of ∆ACM]
∴  C₁ + C₂ =B =  x 
∴ MC is a tangent to the circle at C [converse : tan chord th]

OR

In ∆AMC and ∆ACB:
A₂ = A₁ = 90º  - x                 [= chords subtend = ∠s]
AMC = ACB = 90º               [given]
∴  C₁ + C₂ =B =  x 
∴MC is a tangent to the circle at C [converse : tan chord th]

✓ S  ✓R
✓ S/R
✓ C₂ = 90º - x(5)

✓ S ✓ R
✓✓ C₁ + C₂ = x
✓ R  (5)

✓ S ✓ R
✓✓ C₁ + C₂ = x
✓ R  (5)

10.1.2

In ∆ACB and ∆CMD
B = D₂ = x                     [proved OR exterior ∠  of cyclic quad.]
A₂ = C₂ = 90º -x           [proved OR sum of  ∠s in Δ]
∆ACB ||| ∆CMD            [∠, ∠',∠ ]

OR

In ∆ACB and ∆CMD

B = D₂ = x                     [proved OR exterior ∠  of cyclic quad.]
ACB = AMC = 90º        [given]
∆ACB ||| ∆CMD            [∠, ∠, ∠ ]

OR

In ∆ACB and/en  ∆CMD
B = D₂ = x                     [proved OR exterior ∠  of cyclic quad.]
A2 = C2 = 90º - x          [proved OR sum of  ∠ s in Δ]
ACB = AMC = 90º         [given OR sum of ∠ s in ∆]
∆ACB ||| ∆CMD          

✓ S
✓ S
✓ R (3)

✓ S
✓ S
✓ R (3)

✓ S
✓ S
✓ S (3)

10.2.1

BC = AB     [ΔACB  |||  ΔCMD]
MD   DC
DC = AB     [BC = DC]
MD   DC
∴DC² = AB × MD
In ∆AMC and  ∆CMD
M is common
A₁ = C₂                [tan chord th ]

OR

C1 + C2 = B = D = x                 [tan chord th OR exterior ∠ of cyclic quad]
∆AMC ||| ∆CMD      [∠, ∠ ∠]
AM = CM
CM    MD
∴CM₂ = AM × MD
∴CM₂ = AM ×  MD
  DC₂     AB × MD
= AM
   AB

✓ BC   =     AB
   MD          DC
✓ DC²  = AB × MD
✓ S
✓ S
✓ CM2  =  ²
✓ AM × MD  (6)
    AB × MD

OR
AC = AB                           [∆ACB ||| ∆CMD]
MC   DC
∴CM × AB =  AC × DC
In ∆AMC and  ∆ACB
C = M =  90º    [given]
Â₁ = Â₂          [proven]

OR

ACM = B = x         [proven]
∆AMC ||| ∆ACB    [∠, ∠ ∠]
AC   =    BC
AM        MC
∴AC× MC =  AM × BC
∴ AC = BC.AM  
              MC
CM × AB = BC.AM × DC
                    MC
CM² =  DC .AM × DC   [BC=DC]
                 AB
CM²   =     AM
DC²          AB

✓ AC   =  AB
   MC      DC
✓ S
✓ S
✓ ACMC = AMBC
✓ equating
✓ S (6)

10.2.2

In ΔDMC:
CM = sin x
DC
CM² = sin²x AC = CM
DC²             AB     DC
∴AM = sin²x
  AB                 

OR

In ΔABC:
sin x = AC
           AB
In   ΔAMC:
sin x = AM
           AC
sin x.sin x = AC  × AM   = AM
                    AB     AC      AB

✓  trig ratio
✓ square both sides  (2)

✓ 2 equations for sin x
✓ product  (2)

[16]