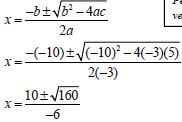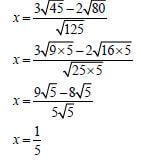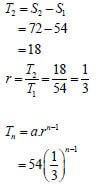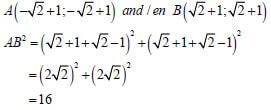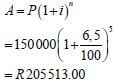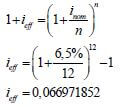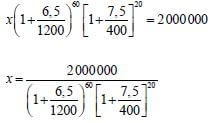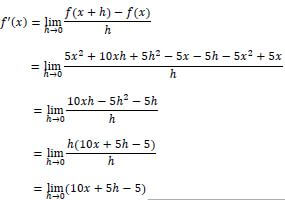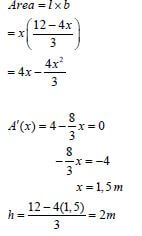MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC EXAMS PAST PAPERS AND MEMOS JUNE 2019
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS
PAPER 1
GRADE 12
NSC EXAMS PAST PAPERS AND MEMOS JUNE 2019
NOTE:
|
MEMORANDUM
QUESTION 1
1.1.1 | x2 - 7x = 0 | ✔ both factors |
1.1.2 | Penalise 1 mark for incorrect rounding off. | ✔ substitution |
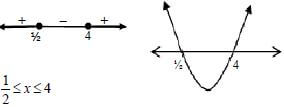
1.1.3 | (2x - 1)(4 - x) ≥ 0 | ✔ critical values |
1.1.4 |
| ✔ squaring both sides |
1.2 | y = -3x + 2.................(1) | ✔ substitution |
1.3.1 |
| ✔ factors under root |
| 1.3.2 | 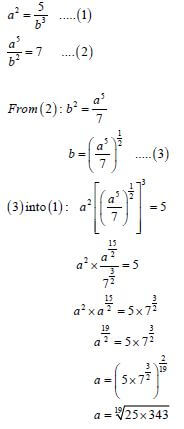 | ✔ equation (3) ✔ substitution ✔ simplification ✔ simplification ✔ isolating a (5) |
QUESTION 2
2.1.1 | 12 ; 9 ; 6 ; . . . . . | ✔ d = –3 |
2.1.2 | Tn = -3(40) + 15 | ✔ substitution |
2.1.3 | S40 = 40/2 (12 + (-105)) = -1860 | ✔ substitution |
2.2.1 | Quadratic Pattern : T1 = 10 | ✔ first differences |
2.2.2 | 2a = 2 3a + b = -7 a + b + c = 10 | ✔ value of a |
2.2.3 | n2 - 10n + 19 = 2019 | ✔ equation |
2.3.1 | Sn = 81 - 81(3)-n | ✔ answer (1) |
2.3.2 |
| ✔ T2 = 18 |
2.3.3 | Yes. | ✔ YES |
2.3.4 | S∞ = a or S∞ =81 - 81(3)-∞ | ✔ substitution |
2.4 |
| ✔ (2x + 3 + 2x + 6 + 2x + 9) |
[27] |
QUESTION 3
3.1 | (let y = 0) Or (let x= 0) | ✔ substitution (y = 0) |
3.2 | x =1 | ✔ answer (1) |
3.3 | y ∈ R\{1} OR y ∈ R but y # 1 | ✔ answer (1) |
3.4 |
| ✔ coordinates of A and B |
3.5 | h(x) = - 2 + 1 | ✔ – ve (reflection) |
[12] |
QUESTION 4
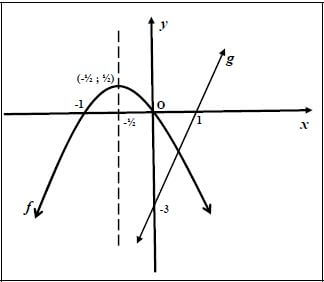
4.1 |
| Parabola Straight line |
4.2 | From sketch -2x2 - 2x > 0 | ✔✔ answer (2) |
4.3 | ST = -2x2 - 2x - (3x - 3) | ✔ ST = –2x2 – 2x – (3x – 3) |
[12] |
QUESTION 5
5.1 | f(x) = 2x k = 2-3 k = 1/8 | ✔ substitution |
5.2 | f-1(x) : x = 2y | ✔ interchanging x and y |
5.3 | f'(x).g(x) ≤ 0 | ✔ method |
[8] |
QUESTION 6
6.1 | | ✔ substitution |
6.2 |  | ✔ substitution |
6.3.1 |
| ✔ formula |
6.3.2 | | ✔ |
[13] |
QUESTION 7
Penalise 1 mark for incorrect notation in the question
7.1 | f(x) = 5x2 - 5x | ✔ 5x2 + 10xh +5h2 - 5x - 5h |
7.2 |
| ✔ |
7.3 | f(-1) = (-1)3 = -1 f(1) = (1)3 = 1 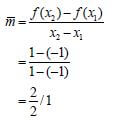 | ✔ f(-1) and f(1) |
[11] |
QUESTION 8
8.1.1 | f(x) = -(2x - 5)(x + 2)2 = 0 | ✔ x-intercepts |
8.1.2 | f(x) = -2x3 - 3x2 + 12x + 20 | ✔ f'(x) |
8.1.3 | mp = -6(-3)2 - 6(-3) + 12 | ✔ gradient |
8.1.4 | T(1 ; y) | ✔ max. value |
8.2.1 | c'(x) -3/2x2 + 6x = 0 | ✔ equating to 0 |
8.2.2 | cn(x0 = -3 + 6 = 0 or x = 0 + 4 | ✔ method |
[18] |
QUESTION 9
9.1 | h = 12 - 4x | ✔✔ answer (2) |
9.2 |
| ✔ substitution |
[8] |
QUESTION 10
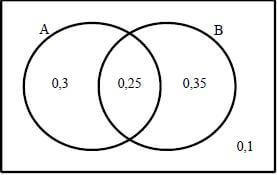
10.1.1 | P(S) = 1 | ✔ 0,3 & 0,25 |
10.1.2 | P(A or B) = P(A) + P(B) - P(A and B) or (from sketch) | ✔ method |
10.1.3 | P(A and B') = 0,3 | ✔✔ answer (2) |
10.1.4 | No : P(A ∩ B) = 0,25 ≠ 0 | ✔ answer (1) |
10.1.5 | P(A ∪ B)' = 0,1 ≠ 0 No : or P(A ∪ B) = 0,9 ≠ 1 | ✔ answer (1) |
10.2.1 | a = 20 | ✔ a = 20 |
10.2.2 | 79 - x + 20 + 19 - x + x + 11 + 16 + 40 - x = 173 | ✔ equation |
10.2.3 | P (at least 2) | ✔ adding correct values |
[15] | ||
TOTAL: 150 |