MATHEMATICS
PAPER 1
GRADE 12 
NSC EXAMS PAST PAPERS AND MEMOS JUNE 2019

INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions. 

1. This question paper consists of TEN (10) questions. Answer ALL the questions.
2. Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in  determining your answers.
3. Answers only will not necessarily be awarded full marks.
4. You may use an approved scientific calculator (non-programmable and non graphical), unless stated otherwise.
5. if necessary, round off answers to TWO decimal places, unless stated otherwise.
6. Diagrams are NOT necessarily drawn to scale.
7. An information sheet, with formulae, is included at the end of the question paper.
8. Number the answers correctly according to the numbering system used in this question  paper.
9. Write neatly and legibly.

QUESTIONS 

QUESTION 1 
1.1 Solve for x, in each of the following: 
1.1.1 x² + 7x = 0 (2)
1.1.2 5 - 10x - 3x² = 0  (correct to TWO decimal places) (3)
1.1.3 (2x - 1)(4 -  x) ≥ 0   (3)
1.1.4  (5)
1.2 Solve simultaneously for x and y in the following equations:   y = 2 - 3x   and x² + y = xy + x (5) 
1.3 1.3.1 Solve for x without the use of a calculator, if: (3) 
1.3.2 Given that, a² = ⁵/_b³   and  a⁵ = ⁷/_b², prove that   (5)  [26]

QUESTION 2 
2.1 Consider the arithmetic sequence: 12 ; 9 ; 6 ; . . .  
2.1.1 Determine the general term, T_n. (2)
2.1.2 Determine the 40^th term. (2)
2.1.3 Determine the sum of the first 40 terms. (2)
2.2 The following information of a quadratic pattern is given: 

• T₁ =10
• The general term of the sequence of first differences is T_n = 2n - 9

2.2.1 Determine the second (T₂) and third (T₃) terms of the quadratic pattern. (3)
2.2.2 Determine the n^th term of the quadratic pattern. (3)
2.2.3 Which term of the quadratic pattern will be equal to 2019? (3)
2.3 In a geometric series the sum is given by, S_n = 81 - 81(3)^-n   
2.3.1 Determine the first term of the series. (1) 
2.3.2 Determine the general term of the series, in the form  T_n = a.r^{n - 1}    (3) 
2.3.3 Is this a convergent series? Give a reason. (2)
2.3.4 Calculate the sum to infinity. (2) 
2.4 Solve for x, if:    (4)   [27]

QUESTION 3 
The diagram below represents the graph of

A and B are the points of intersection between f and its line of symmetry.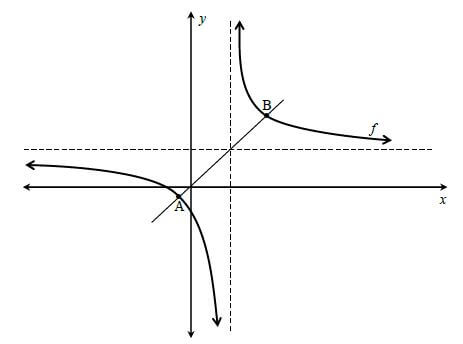  

3.1 Determine the coordinates of the x-intercept and the y-intercept of the graph. (4)
3.2 Write down the equation of the vertical asymptote. (1)
3.3 Write down the range of f . (1)
3.4 Calculate the distance AB, between the two points of symmetry. (4) 
3.5 The graph of y y = f(x) is transformed to g(x) by a reflection in the x-axis followed by  a shift of 4 units in the positive x-direction. Determine the equation of g(x). (2) [12]

QUESTION 4 
Given the equations f(x) = −2x² - 2x   and g(x) = 3x - 3, answer the following questions. 
4.1 Draw sketch graphs of f and g on the same system of axes. Clearly indicate the  co-ordinates of the turning point, the axis of symmetry and the intercepts with the  axes. (6) 
4.2 Hence, or otherwise, determine the values of x for which f (x) > 0. (2) 
4.3 ST is a vertical line segment between the two graphs parallel to the y-axis, with S on  the parabola and T on the straight line. Determine the maximum vertical distance  between the two graphs for .(4)   [12] 

Related Items

QUESTION 5 

The diagram represents sketch graphs of the functions, f(x) = 2^x , with P(– 3 ; k) a point  on the curve, and g(x) = 2x + 1

5.1 Find the value of k. (2) 
5.2 Determine the equations of f^-1  and g^-1.     (in the form y = . . . ) (4) 
5.3 For which values of x will f'(x).g(x) ≤ 0?     (2) [8] 

QUESTION 6 
6.1 Paul invested R150 000 for 5 years at an interest rate of 6,5% per annum compounded  annually. How much money will he get at the end of the five years? (2) 
6.2 A bus is purchased for R975 000. Calculate the rate of depreciation of the value of the bus if its trade-in value, 7 years later, is R134 000 on the reducing-balance method. (3) 
6.3 Vivian wants to have saved R2 000 000 ten years from now. The interest rate for the  first five years is 6,5% p.a. compounded monthly, and then 7,5% p.a. compounded  quarterly, for the last five years.  
6.3.1 Determine the effective interest rate for the first five years. (3) 
6.3.2 How much does she have to invest initially to achieve this target? (to the  nearest rand) (5) [13] 

QUESTION 7 
7.1 Determine the first derivative of f(x) = 5x² - 5x from first principles. (5) 
7.2 Determine:   (3)
7.3 Given: g(x) = x³
Determine the average gradient of g between the points A and B, with x-coordinates  –1 and 1 respectively. (3) [11]

QUESTION 8 
8.1 Sketched below is the graph of g(x) = −2x³ - 3x² + 12x + 20 = (2x - 5)(x + 2)² . A and T are the turning points of g. P(−3;11)  is a point on the graph. y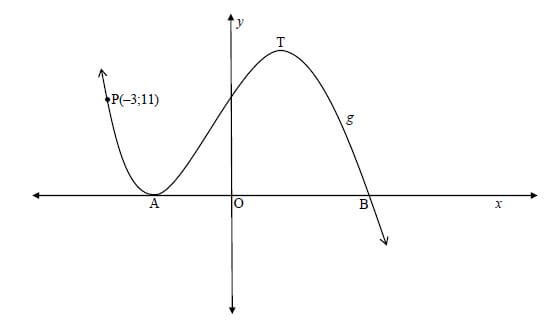 

8.1.1 Determine the length of AB. (2)
8.1.2 Determine the x-coordinate of T. (3)
8.1.3 Determine the equation of the tangent to g at P(–3 ; 11) in the form of y = . . . (3) 
8.1.4 Determine the value(s) of k for which −2x³ - 3x² + 12x + 20 = k has three  distinct roots. (3) 
8.2 c(x)  is a cubic function with   (3)
8.2.1 For which values of x will the graph of c(x) be increasing? (3) 
8.2.2 Discuss the concavity of the graph of c(x). (4) [18]

QUESTION 9 
A window frame consisting of 6 identical rectangles is illustrated below. 12 metres of aluminium material is used for the frame. The width of the frame is x metres and the height  h metres.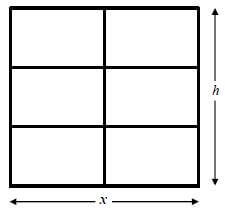 

9.1 Express the height, h, of the frame in terms of x. (2) 
9.2 Determine the dimensions of the frame so that the area of the window is a maximum. (6) [8]

QUESTION 10 
10.1 For two events, A and B, in the sample space, S, it is given that P(A) = 0,55 ;  P(B) = 0,6 and P(A and B) = 0,25 
10.1.1 Draw a Venn diagram to represent the above information. (3)
10.1.2 Determine P(A or B) (2)
10.1.3 Determine P(A and B') (2) 10.1.4 Are the events mutually exclusive? Give a reason for your answer. (1)
10.1.5 Are the events exhaustive? Give a reason for your answer. (1) 
10.2 Complaints about a restaurant fell into three main categories: the menu (M), the food  (F) and the service (S). In total, 173 complaints were received in a certain month. The  complaints were as follows and illustrated in the diagram below. 

• 110 complained about the menu
• 55 complained about the food 
• 67 complained about the service 
• 20 complained about the menu and the food, but not the service 
• 11 complained about the menu and the service, but not the food 
• 16 complained about the food and the service, but not the menu
• The number who complained about all three is unknown 

10.2.1 Write down the values of a and b. (in terms of x where necessary) (2)
10.2.2 Determine the number of people who complained about ALL three categories. (2) 
10.2.3 Determine the probability that a complaint selected at random from those  received, complained about AT LEAST TWO of the categories. (2) [15] 

TOTAL: 150 

INFORMATION SHEET: MATHEMATICS