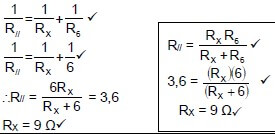PHYSICAL SCIENCES PHYSICS PAPER 1 GRADE 12 MEMORANDUM - AMENDED SENIOR CERTIFICATE EXAM PAST PAPERS AND MEMOS MAY/JUNE 2016

More in this category: « PHYSICAL SCIENCES CHEMISTRY PAPER 2 GRADE 12 MEMORANDUM - AMENDED SENIOR CERTIFICATE EXAM PAST PAPERS AND MEMOS MAY/JUNE 2016 PHYSICAL SCIENCES PAPER 2 GRADE 12 - NSC PAST PAPERS AND MEMOS SEPTEMBER 2016 »

Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

Physical Sciences (Physics)
Paper One (P1)
Grade 12
Amended Senior Certificate Exam Past Papers And Memos
May/june 2016

Memorandum

QUESTION 1
1.1 A✓✓ (2)
1.2 B✓✓ (2)
1.3 D✓✓ (2)
1.4 C✓✓ (2)
1.5 B✓✓ (2)
1.6 B✓✓ (2)
1.7 A✓✓ (2)
1.8 D✓✓ (2)
1.9 C✓✓ (2)
1.10 D✓✓ (2)

[20]

QUESTION 2

2.1 A body will remain in its state of rest or motion at constant velocity ✔unless a resultant/net force✔ acts on it.
OR
Every body continues in its state of rest or of uniform motion in a straight line ✔unless a resultant/net force ✔acts on it. (2)

2.2 0 (N)✔/zero/nul (newton)
NOTE: No penalisation if the unit is omitted (1)

2.3

Accepted labels
w	F_g / F_w / weight / mg / gravitational force
T	F_T / tension F_s / spanning
15 N	F_a / F15N / F_applied / F_t / F_toegepas / F

Accept

OR
(3)

Notes

Mark awarded for label and arrow
Do not penalise for length of arrows since drawing is not to scale.
Any other additional force(s) Minus 1 (-1) mark
If force(s) do not make contact with body: Minus 1 (-1) mark
Minus 1 mark if all arrows are omitted but correctly labelled

2.4 (7)

2 kg block
F_net = ma
F_a + F_g + (-T) = ma
F_a + m_g + (-T) = ma (upto to this point ✔ )
[15 + (2)(9,8) – T]✔ = (2)(1,2)✔
T = 32,2 N

10 kg block
T + (-f_k) = ma
T - μkN = ma
T - μkmg = ma ✔
32,2 - (μk)(10)(9,8)✔ = (10)(1,2)✔
μk = 0,21✔

NOTE:L
If fk is calculated separately – award one mark.

Massless string approximation/Systems approach (4/7)
F_net = ma✔
FA – fk + w = (M + m)a
15 – μkMg + mg = (M + m)a
15 - μk(10(9,8) + (2)(9,8)✔ = (10 + 2)(1,2)✔
μk = 0,21✔

2.5 Smaller than ✔ (1)
2.6 Remains the same ✔ - The coefficient of kinetic friction is independent of the (apparent microscopic) surface areas in contact. ✔

The coefficient of kinetic friction depends only on the type of materials used✔ (2)

[16]

QUESTION 3
3.1 An object upon which the only force✔ acting is the force of gravity.✔
ACCEPT
An object that falls freely ✔with an acceleration of (g) 9,8 m∙s^-2 ✔
An object that is launched ✔(or synonyms) with an initial velocity under the influence of the force of gravity.✔ (2)
3.2.1 (4)

OPTION 1

Upward positive

v_f = v_i + aΔt ✔
-30 = 30✔ + (-9,8)Δt✔
Δt = 6,12 s✔

Downward positive

v_f = v_i + aΔt ✔
30 = -30✔ + (9,8)Δt✔
Δt = 6,12 s✔

OPTION 2

Upward positive

v_f = v_i + aΔt ✔
0 = 30✔ + (-9,8)Δt✔
Δt = 3,06 s
Total time/ = (2)(3,06) = 6,12 s ✔

Downward positive

v_f = v_i + aΔt ✔
0 = -30✔ + (9,8)Δt✔
Δt = 3,06 s
Total time = (2)(3,06) = 6,12 s ✔

OPTION 3

Upward positive

Δy = v_iΔt + ½ aΔt²✔
0 = (30) Δt✔ +½ (-9,8)Δt2✔
Δt = 6,12 s✔

Downward positive

Δy = v_iΔt + ½ aΔt²✔
0 = (-30) Δt✔ +½ (9,8)Δt2✔
Δt = 6,12 s✔

OPTION 4

Upward positive

F_net∆t = ∆p = (mv_f – mv_i)✔
mg∆t = m(v_f – v_i)
9,8∆t✔ = (30-(-30))✔
Δt = 6,12 s✔

Downward positive

F_net∆t = ∆p = (mv_f – mv_i)✔
mg∆t = m(v_f – v_i)
-9,8∆t ✔= (-30-30)✔
Δt = 6,12 s✔

OPTION 5

Upward positive

From top to bottom
vf = v_i + aΔt ✔
-30 = 0 ✔+ (-9,8)Δt✔
Δt = 3,06 s
Total time = 2(3,06)
= 6,12 s✔

Downward positive

From top to bottom
v_f = v_i + aΔt ✔
30 = 0✔ + (9,8)Δt✔
Δt = 3,06 s
Total time = 2(3,06)
= 6,12 s✔

3.2.2

POSITIVE MARKING FROM QUESTION 3.2.1

OPTION 1
Upward positive

Δy = v_iΔt + ½ aΔt² ✔
Δylast= Δy(6,12)- Δy(5,12)
= {30(6,12) +½ (-9,8)(6,12)²}✔- {30 (5,12) +½ (-9,8)(5,12)²}✔ = -25,076
Distance = |Δy| = 25,08 m✔

POSITIVE MARKING FROM QUESTIONS 3.2.1
Downward positive

Δy = v_iΔt + ½ aΔt² ✔
Δylast= Δy(6,12)- Δy(5,12)
= {-30(6,12) +½ (9,8)(6,12)²}✔- {-30(5,12) +½ (9,8)(5,12)²}✔
= 25,076
Distance = |Δy| = 25,08 m✔

OPTION 2
Upward positive

v_f = v_i + aΔt
= 0 + (-9,8)(2,06) ✔
= -20,188 m∙s^-1

Δy = v_iΔt + ½ aΔt² ✔
= (-20,188)(1) + ½ (-9,8)(1)² ✔
= -25,09 m
Distance = |Δy| = 25,09 m ✔

Δy = v_f + v_i _Δt✔
2
= -20,188 + (-30) _(1)✔
2
= -25,09 m
Distance = |Δy| = 25,09 m ✔

v_f² = v_i² + 2aΔx ✔
(-30)2 = (-20,188)2 + 2(-9,8)Δx✔
Δx = -25,12 m
Distance = |Δy| = 25,12 m ✔

Downward positive

v_f = v_i + aΔt
= 0 + (9,8)(2,06)✔
= 20,188 m∙s^-1

Δy = viΔt + ½ aΔt²✔
= (20,188)(1) + ½ (9,8)(1)² ✔
= 25,09 m
Distance = |Δy| = 25,09 m✔

Δy = v_f + v_i _Δt✔
2
= 20,188 + 30 _(1)✔
2
= 25,09 m
Distance = |Δy| = 25,09 m✔

OR/OF

v_f² = v_i² + 2aΔx ✔
(30)2 = (20,188)2 + 2(9,8)Δx✔
Δx = 25,12 m
Distance = |Δy| = 25,12 m✔

OPTION 3

v_f = v_i + aΔt
= 0 + (-9,8)(2,06)✔
= -20,188 m∙s^-1

Δy = v_f + v_i _Δt✔
2
= -20,188 + 30 _(5,12)✔
2
= -25,12 m
Distance= |Δy| = 25,12 m✔

v_f = v_i + aΔt
= 0 + (9,8)(2,06)✔
= 20,188 m∙s^-1

Δy = v_f + v_i _Δt✔
2
= 20,188 - 30 _(5,12)✔
2
= -25,12 m

Distance = |Δy| = 25,12 m✔

OPTION 4
Upward positive
Distance travelled in the first second = distance travelled in the last second

Δy = v_iΔt + ½ Δt² ✔
= (30)(1) + ½ (-9,8)(1)² ✔
= 25,1 m ✔
Distance = |Δy| = 25,1 m ✔

Downward positive
Distance travelled in the first second = distance travelled in the last second

Δy = v_iΔt + ½ Δt²✔
= (-30)(1) + ½ (9,8)(1)² ✔
= -25,1 m ✔
Distance = |Δy| = 25,1 m ✔

(4)

3.3 (4)

POSITIVE MARKING FROM QUESTION 3.2.1

Upward positive

Δy = v_iΔt + ½ aΔt²✔
-50✔= [v_i (4,12)] + [½ (-9,8)(4,12)²]✔ vi = 8,05 m∙s^-1speed = 8,05 m∙s^-1✔

Downward positive

Δy = v_iΔt + ½ aΔt2✔

50✔= v_i (4,12) + [½ (9,8)(4,12)²]✔ vi = - 8,05 m∙s^-1

speed/spoed = 8,05 m∙s^-1✔

3.4

POSITIVE MARKING FROM QUESTIONS 3.2.1 AND 3.2.2
Upward positive

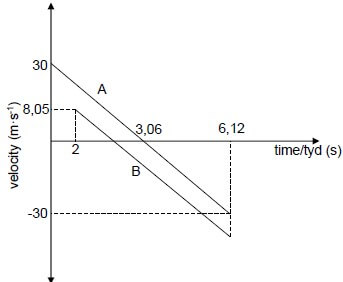
Criteria	Marks
Correct shape of A	✔
Correct shape of Graph B parallel to A below A	✔
Time at which both A and B reach the ground (6,12 s)	✔
Time for A to reach the maximum height (3,06 s) shown	✔

NOTE :
Do not penalise if velocities are not indicated
3.4

POSITIVE MARKING FROM QUESTIONS 3.2.1 AND 3.2.2
Downward positive

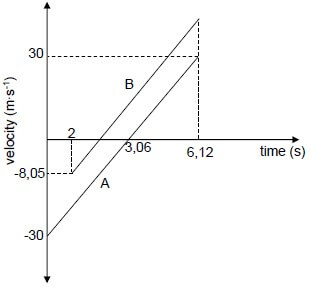
Criteria	Marks
Correct shape of A	✔
Correct shape of Graph B parallel to A above A	✔
Time at which both A and B reach the ground (6,12 s)	✔
Time for A to reach the maximum height (3,06 s) shown	✔

(4)
[18]

QUESTION 4
4.1 The total (linear) momentum of an isolated (closed) system ✔is constant (is conserved) ✔

In an isolated (closed) system, the total (linear) momentum ✔before collision is equal to the total linear momentum after collision. ✔ (2)

4.2.1 (4)

∑p_i = ∑p_fm1 v_1i + m2v_2i = m₁ v1_f + m2v2_f
m1 v1_i + m2v_2i = (m₁ + m2)v_f
1 mark for any
(5)(4) + (3)(0) ✔ = (5 + 3)v_f✔
∴ v = 2,5 m∙s^-1 ✔

Δp_5kg = -Δp_3kg ✔
mv_f - mv_i = mv_f - mv_i
5vf – (5)(4)✔ = 3vf – (3)(0) ✔
v_f = 2,5 m∙s^-1 ✔

4.2.2 (4)

OPTION 1
POSITIVE MARKING FROM QUESTION 4.2.1

Fn_et∆t = ∆p = (p_f – p_i) = (mv_f – mv_i) ✔
F_net(0,3) ✔ = 8 [(0 – (2,5)]✔
F_net = - 66,67 N
∴ _Fnet = 66,67 N✔

OPTION 2
POSITIVE MARKING FROM 4.2.1
F_net = ma ✔

= m (v_f- v_i)✔
Δt

= 8 (0 - 2,5) ✔= - 66,67 N
0,3✔
∴ F_net = 66,67 N✔

OPTION 3
POSITIVE MARKING FROM 4.2.1
v_f = v_i + a∆t
0 = 2,5 + a(0,3) ✔
a = - 8,333 m·s^-2
F_net = ma ✔
= 8 (-8,333) ✔
= - 66,67 N
∴ F_net = 66,67 N✔

OPTION 4

W_net = ΔEk
F_netΔxcosθ = ½ m(v_f² – v_i²)

F_net (V_f + V_i) Δt cos 180º = ½m(Vf² - Vi²)✔
2
Fnet (2,5 + 0) (0,3) (-1)✔= ½(8)(0² - 2,5⁵)✔
2
Fnet = 66,67 N✔

[10]

QUESTION 5
5.1 The total mechanical energy in an isolated (closed) system ✔remains constant (is conserved). ✔
NOTE

If total or isolated/closed is omitted (max: 1/2 ) (2)

5.2.1 (3)

W = F∆x cosθ✔
= (30)( 5 )cosθ
sin30º
= (30)(10)cos180º
= (30)(10)(-1) ✔
= - 300 J✔

5.2.2 (5)

OPTION1
POSITIVE MARKING FROM 5.2.1
W_nc = ΔE_P+ ΔE_K
W_nc = mg(h_f - h_i) + ½ m(v_f² - v_i² ) ✔
- 300 ✔= (20)(9,8)(0 - 5) ✔+ ½ (20)(v_f² –0) ✔
v = 8,25 m∙s^-1✔

OPTION 2
POSITIVE MARKING FROM 5.2.1

W_net = ΔE_KW_g + W_f = ½m(v_f² - v_i² ) ✔
Wg + (-300) = ½ (20)(v_f² -0)✔
5
[(20)(9,8)sin30º ⁵/ _0,5 cos 0 ] ✔ + (- 300) ✔ = 10v_f²vf = 8,25 m∙s^-1✔

5.3 (4)

F = w// + f
= (100)(9,8)sin30º + 25 ✔
= 515 N

P_ave = Fv_ave ✔
= (515)(2)✔
= 1 030 W✔

[14]

QUESTION 6
6.1 X ✓ (1)
6.2 As ambulance approaches the hospital the waves are compressed✓or wavelengths are shorter. Since the speed of sound is constant✓ the observed frequency must increase✓. Therefore the hospital must be located on the side of X (from v = fλ)

The number of wave fronts per second reaching the observer are more at X✓✓. For the same constant speed, this means that the observed frequency increases ✓therefore the hospital must be located on the side of X. (from v = fλ) (3)
6.3 (5)

f_L= V ± V_L f_S OR F_L = V F_S✔
V ± V_S V - V_S
f_L= 304 ✔ (400)✔
(340 -✔ 30)

f_L = 438,71 Hz✔

NOTE:
If any other value for the speed of sound is used subtract 2 marks. One for substitution and one for answer

6.4 (3)

v = fλ✔
340 = 400λ✔
λ = 0,85 m✔

[12]

QUESTION 7
7.1 (3)

n = ^Q / _e✓
= -32×10-⁹ ✓
  -1,6×10-¹⁹
= 2 x 10¹¹✓electrons
NOTE:
Answer must be positive (-1 mark)

n = ^Q / _e✓
= -32×10^-⁹ ✓
-1,6×10^-19
= 2 x 10¹¹✓electrons

7.2 (3)

Accepted label
w	F_g/F_w/weight/mg/gravitational force
T	FT/tension Fs/spanning
FE	Felectrostatic/F_Q1Q2 /Coulomb force/F

7.3 (5)

F_net = 0
mg + F_E = T
mg + k Q₁Q₂ ✔ - T = 0
r²
(0,007)(9,8)✔ +(9 × 10⁹ )( 32 × 10⁹ )( 55 × 10⁹) ✔ = T
(0,025)²✔
∴T = 9,39(4) x 10^-2 N✔ (Accept: 0,1 N)

ACCEPT

F_E = w_Q2 ✔
(0,007)(9,8) ✔+ (0,007)(9,8)✔✔ = T
T = 0,137 N ✔

[11]

QUESTION 8
8.1 The (electrostatic) force experienced by a unit positive charge (placed at that point).✔✔
NOTE:
If the words “unit positive” is omitted (max 1/2) (2)

8.2 (2)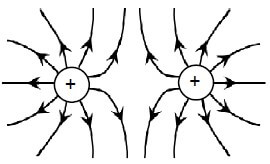

8.3 (3)

Guideline for allocating marks
	Lines must not cross / Lines must touch the spheres but not enter spheres	✔
	Arrows point outwards	✔
	Correct shape	✔

(5) ↓

E =kQ ✔
r²
E_Q1X = ( 9×10⁹)(30 ×10^-6)✔
(x )²
E_Q2X = ( 9×10⁹)(45 ×10^-6)✔
(0,15+ x )²E_net = 0

E_Q1X = E_Q2X
( 9×10⁹)(30 ×10^-6)✔ = ( 9×10⁹)(45 ×10^-6)
(x )² (0,15+ x )²

✔For equating equations

5,477 = 6,708
x 0,15 + x
x = 0, 67 m (0,667 m) ✔

[10]

QUESTION 9
9.1.1 (3)

OPTION 1

P = V² / _R✔
4 = V² / _R=(12)² / R✔

R = 36 Ω✔

OPTION 2

P = VI
4 = I(12)
I = 0,33...A

V = IR✔
12 = 0,33R✔
R = 36,36 Ω✔

OPTION 3

P = V I
4 = I(12)
I = 0,33 ..A

P = I2 R ✔
4 = (0,332) R✔
R = 36,73 Ω✔

9.1.2 Increase✔ (1)
9.1.3 No change✔ - Same potential difference✔ (and resistance) (2)
9.2.1 (4)

V = IR ✔
5 = I(6) ✔
∴ I = 0,83 A

V_”lost” = Ir OR ε= I(R + r)
1 = (0,83)r ✔ 6 = (0,83)(6 + r) ✔
r = 1,20 Ω✔ r = 1,23 Ω✔

9.2.2 Work done ✔in moving a unit charge ✔ through a cell.
ACCEPT
Energy transferred per unit charge/ Work done in moving in 1 C of charge. (2)
9.2.3

OPTION 1
POSITIVE MARKING FROM 9.2.1
V_”lost” = Ir
1,5✔ = I(1,2)
I = 1,25 A

V|| = I₆R₆
4,5 = I₆(6)✔
I₆ = 0,75 A

Vx = IRx✔ OR V = IR
4,5 = (1,25 – 0,75)R_x✔
Rx = 9 Ω✔

OPTION 2
POSITIVE MARKING FROM 9.2.1

V_”lost” = Ir
1,5✔ = I(1,2)
I = 1,25 A

V|| = I_pR_p
4,5 = (1,25)Rp✔
R_p = 3,6 Ω

RX = 9 Ω✔

(5)
[17]

QUESTION 10
10.1.1 a to b ✔ (1)
10.1.2 Fleming's left hand rule /Left hand motor rule✔
ACCEPT

Right hand rule (1)

10.1.3 Split rings /commutator ✔ (1)
10.2.1 Mechanical/Kinetic energy to electrical energy. ✔✔ (2 or/of 0) (2)

10.2.2 (5)

OPTION 1

V_rms = V_max_✔
√2
= 430 ✔
√2
= 304,06 V

I = ^V/_R✔

= ^304,06/_400 ✔ = 0,76 A✔

OPTION 2

Vm_ax = I_maxR ✔
430 = I_max(400) ✔

_Irms = I_max_✔
√2
= 1,075 ✔
√2

= 0,76 A✔

OPTION 3

V_rms = V_max_✔
√2
= 430 ✔
√2
= 304,06 V
P_average = V2_rms = (304,06)²
R 400
= 231,13 W
Pa_ve = I_rmsV_rms✔
231,13 = I_rms (304,06) ✔
I_rms = 0,76 A✔

OPTION 4

V_rms = V_max_✔
√2
= 430 ✔
√2
= 304,06 V
P_average = V2_rms = (304,06)²
R 400
= 231,13 W

P_ave = I²_rmsR✔

231,13 = I²_rms (400) ✔

I_rms = 0,76 A✔

[10]

QUESTION 11
11.1.1 It tells us that light has a particle nature.✔ (1)
11.1.2 Remain the same. ✔ - For the same colour/ frequency/wavelength the energy of the photons will be the same✔. (The brightness causes more electrons to be released, but they will have the same maximum kinetic energy.)

Intensity only affects the number of ejected photo-electrons and not the maximum kinetic energy or maximum speed of the ejected photo-electrons

Maximum kinetic energy of ejected photo-electrons is independent of intensity of radiation (2)

11.1.3 (5)

E = W₀ + E_k
hf = hf₀ + E_k
hf = hf₀ + ½ mv²
E = W₀ + ½ mv²
Any one✔
(6,63 10^-34)(3 × 10⁸) ✓ = (6,63 × 10^-34)(3 × 10⁸)^{^✓+ ½ (9,11 10^-31)(4,76 × 10⁵}⁾^{^2✓} 420 ×10^-9 λo
λo = 5,37 x 10-7 m
∴ the metal is sodium ✓

11.2 Q✓ and/en S ✓ - Emission spectra occur when excited atoms /electrons drop from higher energy levels to lower energy levels. ✓✓ (4)

[12]
TOTAL: 150

Last modified on Tuesday, 15 June 2021 08:04

Published in Grade 12 Amended Senior Certificate Exam Past Papers and Memos 2016

PHYSICAL SCIENCES PHYSICS PAPER 1 GRADE 12 MEMORANDUM - AMENDED SENIOR CERTIFICATE EXAM PAST PAPERS AND MEMOS MAY/JUNE 2016

Memorandum

Related items