NATIONAL SENIOR CERTIFICATE
GRADE 12
SEPTEMBER 2020
TECHNICAL MATHEMATICS P1

INSTRUCTIONS AND INFORMATION

Read the following instructions carefully before answering the questions.

1. This question paper consists of NINE questions.
2. Answer ALL the questions.
3. Answer QUESTIONS 4.1.5 and QUESTION 7.5 on the ANSWER SHEETS provided.
   Write your name and school name in the spaces provided on the ANSWER SHEETS and hand in the ANSWER SHEETS with your ANSWER BOOK.
4. Number the answers correctly according to the numbering system used in this question paper.
5. Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
6. Answers only will NOT necessarily be awarded full marks.
7. You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
8. If necessary, round off answers to TWO decimal places, unless stated otherwise.
9. Diagrams are NOT necessarily drawn to scale.
10. An information sheet with formulae is attached at the back of the question paper.
11. Write neatly and legibly.

QUESTION 1

1.1 Solve for x:
1.1.1    0 = (3? − 2)(? + 1)     (2)
1.1.2    7x² + 9x − 4 = 0 (correct to TWO decimal places) (4)
1.1.3   −6x² < 5x        (4)
1.2 Solve the following systems of equations simultaneously:
x + 3y = 1 and 2x² + 2y² = −5xy      (7)
1.3 The angular velocity of a compressor pulley is 5,425 revolutions per minute.
1.3.1 Convert the angular velocity of the compressor pulley to revolutions per second. (1)
1.3.2 Write the angular velocity in QUESTION 1.3.1 in Scientific Notation. (1)
1.4 Convert 101111₂ to decimal notation, WITHOUT using a calculator. (2)
[21]

QUESTION 2

Determine:
2.1 The nature of the roots of: −x² + 9x − 2 = 0  (3)
2.2 The value(s) of c for which the roots of −x² + 9x + c = 0 will be imaginary. (4)
[7]

QUESTION 3

3.1 Simplify without the use of a calculator (show all steps):
3.1.1      (4)

3.1.2 ³√− ( 27)x⁶ + √(25x⁴)     (3)
3.1.3  log ₂ 32 ÷ 2 log ₅ 25        (3)
3.2 Solve for x if:
log ₂ (8x³ −  1) −  log100 =  log ₂(4x² + 2x + 1)  (5)
3.3 Express the complex number z = − 3 + i √3 in the polar form z =r (cosα + is in α)   (5)
3.4 Solve for x and y if: y −  i = 3xi    (4)
                                      2 −  i
[24]

QUESTION 4

4.1 Given the function ƒ(x) = − ⁶/_x + 2 and g(x) = x² −  x −  6
4.1.1 Calculate the x-intercept of ƒ.        (2)
4.1.2 Determine the x-intercepts of g.     (3)
4.1.3 Write down the y-intercept of g.      (1)
4.1.4 Write down the equation(s) of the asymptotes of ƒ.   (2)
4.1.5 Determine the coordinates of the turning point of g.   (3)
4.1.6 Sketch the graphs of ƒ and g on the ANSWER SHEET provided, indicating the asymptote(s) , turning point and intercept(s) on the graphs.   (6)
4.1.7 Write down the domain of ƒ.     (1)
4.1.8 Use the sketch to determine the value(s) of x > 1 for which ƒ(x) ≤ g (x)      (1)
4.2 Sketched below are the graphs of ƒ(x) = 2^X + q and g(x) = – √(r² −  x²), intersecting at (0;–2), their common y-intercept. Point A is the x-intercept of ƒ.

Determine:
4.2.1 The equation of g        (2)
4.2.2 The value of q             (2)
4.2.3 The coordinates of A   (3)
4.2.4 The range of ƒ            (1)
[27]

QUESTION 5

5.1 An asset worth R800 000 depreciated once off at a rate of 8,8%. Determine the current value of the asset. (1)
5.2 The graph below represents the number of people infected during the 21 days of Covid-19 lockdown on an island.
The dotted line shows the number of infected people, on the 7^th day of lockdown.

5.2.1 Write down the number of infected people on the island at the beginning of the lockdown period. (1)
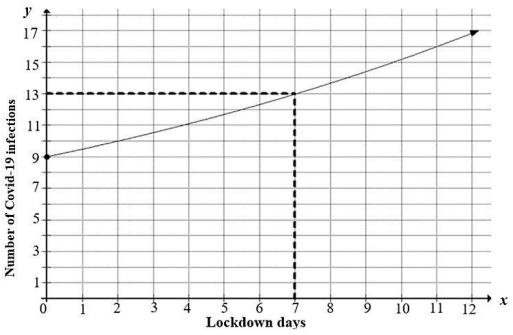
5.2.2 Determine the daily compounded growth rate of infections on the island at the end of the first week of lockdown. (3)
5.2.3 On the 7th day, the average compound growth rate of infections dropped by2%.
Determine the number of days for which the number of infected people was more than double just before the lockdown period started on the island.   (3)
5.3 Mr Nanaka invested a certain amount of money into a savings account. During the first 4 years the interest rate was 6,5% per annum, compounded monthly. At the end of 4 years the interest rates increased to 7% per annum, compounded half yearly, until the
end of the investment period.
Determine, showing ALL calculations, the initial amount that was invested, if the investment grew to R800 000 at the end of the 10-year investment period. (5)
[13]

QUESTION 6

6.1 Determine the derivative of ƒ(x) = −½x + π  by using FIRST PRINCIPLES.     (5)
6.2 Determine:
6.2.1  D_x (9π − ¹⁴/_√x)      (3)
6.2.2  ^dy/_dx if 2xy + x = x⁻⁹           (4)
6.3 The vertical change in the y-coordinates corresponding to x = −2 and x = x₁ on the graph of h (x) = x² − 4 is −3.
Determine the possible value(s) of x₁ if the average gradient between two points is 1. (4)
[16]

QUESTION 7

Given : h (x) = 2x³ + x² − 5x + 2:

7.1 Determine the y-intercept of h        (1)
7.2 Show that x = ½ is the x-intercept of h.      (2)
7.3 Hence or otherwise, determine all the other x-intercepts of h. (3)
7.4 Determine the coordinates of the turning points of h.   (5)
7.5 Sketch the graph of h on the ANSWER SHEET provided, showing all the intercepts and the turning points of h. (5)
7.6 Determine the equation of the tangent to the graph of h at x = 0. (4)
[20]

QUESTION 8

The picture below shows water ejection from a stationary fire extinguishing truck. Ignoring all other factors, the curve formed by the water represents a parabolic function (S) defined by S(t) = 3 + 6t − (¾t²); t ∈ [0;8,5], where S is the height of the water in metres relative to the point of ejection by the truck and t is the time taken in seconds.

8.1 Write down the height of the fire extinguishing truck.                  (1)
8.2 Determine the height of the water after 2 seconds of ejection.    (2)
8.3 Determine the time, in seconds, the water took to reach the maximum height.  (3)
8.4 Hence, or otherwise, show by means of relevant calculations whether the truck would be suitable to extinguish fire in a building floor that is 16 m above the ground level.   (4)
[10]

QUESTION 9

9.1 Determine the following integrals:
9.1.1   ∫(y⁵√x)dx                 (3)
9.1.2   ∫(¹/_x − ⁵/x² ) dx        (3)
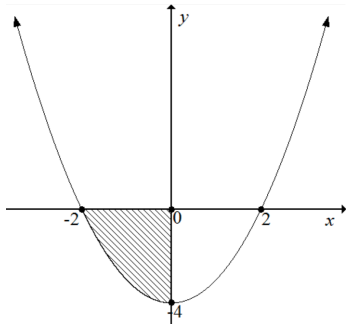
9.2 The sketch below shows the shaded bounded area of the curve of the function  defined by g(x) = x² – 4.

Determine (showing ALL calculations) the shaded area bounded by the curve g and the x-axis between the points where x = −2 and x = 0.   (6)
[12]
TOTAL: 150

ANSWER SHEET

QUESTION 4.1.5

QUESTION 7.5

INFORMATION SHEET: TECHNICAL MATHEMATICS

,