Mathematical Literacy P2 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupINSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of FOUR questions. Answer ALL the questions.
- Use the ADDENDUM with ANNEXURES for the following questions:
ANNEXURE A for QUESTION 1.1
ANNEXURE B for QUESTION 1.3
ANNEXURE C for QUESTION 2.1
ANNEXURE D for QUESTION 4.1
ANNEXURE E for QUESTION 4.2
Write your NAME and GRADE in space provided on the ANSWER SHEET for QUESTION 3.2.5. Hand your ANSWER SHEET in with your ANSWER BOOK. - Number the questions correctly according to the numbering system used in this question paper.
- You may use an approved calculator (non-programmable and non-graphical), unless stated otherwise.
- Show ALL calculations clearly.
- Maps and diagrams are NOT drawn to scale, unless otherwise stated.
- Indicate units of measurement, where applicable.
- Round off ALL final answers appropriately accordingly to the given context, unless stated otherwise.
- Start EACH question on a NEW page.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Ayryn bought a house in 2018. She decided to draw up a loan model for the duration of the loan period as shown in ANNEXURE A (some information has been omitted). Use the information in ANNEXURE A (TABLE 1) to answer the questions below.
1.1.1 Show, with calculations, how the interest amount of R6 088,06 for month 3 was calculated. (3)
1.1.2 The bank uses the following Home Loan Factor Table to calculate the monthly repayments on home loans:
TABLE 2: Home Loan Factor Table 2018
| Years | ||||||
| 5 | 10 | 15 | 20 | 25 | 30 | |
| Interest % | Factor | |||||
| 9,00% | 20,76 | 12,67 | 10,14 | 9,00 | 8,39 | 8,05 |
| 9,25% | 20,88 | 12,80 | 10,29 | 9,16 | 8,56 | 8,23 |
| 9,50% | 21,00 | 12,94 | 10,44 | 9,32 | 8,74 | 8,41 |
| 9,75% | 21,12 | 13,08 | 10,59 | 9,49 | 8,91 | 8,59 |
| 10,00% | 21,25 | 13,22 | 10,75 | 9,65 | 9,09 | 8,78 |
| 10,25% | 21,37 | 13,35 | 10,90 | 9,82 | 9,26 | 8,96 |
[Adapted from http://capetownproperty.blaauwberg.net]
Use TABLE 2 above with TABLE 1 in ANNEXURE A and show how the monthly repayment was calculated.
NOTE:
- Monthly repayments are calculated by dividing the home loan amount by 1 000 and multiplying by the factor.
- The factor used depends on the number of years and the interest rate. (3)
1.1.3 Calculate the closing balance of month 3. (2)
1.1.4 Ayryn stated if she had chosen a shorter period, her monthly repayment would have been less. Refer to the loan factor table and briefly explain, without calculations, whether Ayryn’s statement is valid or not. (3)
1.1.5 A friend told Ayryn that after 119 repayments, she will already have paid R15 000 more than the original home loan amount. Verify, with the necessary calculations, whether this statement is valid or not. (5)
1.1.6 What effect will an increased monthly repayment have on the total interest she has to pay on her home loan? (2)
1.2
Ayryn wants to extend one of her rooms. The extension will be 2 metres by 2 metres. The builder must lay the concrete floor before the building can start. The builder will use the chart as shown below as a guideline.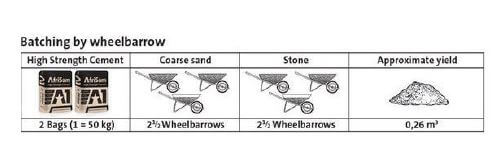 [Source: http://pinterest.com] The height of the concrete floor is 300 mm. |
1.2.1 Calculate the volume of the concrete floor in cubic metres (m3) that must be filled with concrete.
You may use the formula:
Volume = Length × Breadth × Height (3)
1.2.2 Determine how many bags of cement should be used for the volume calculated in QUESTION 1.2.1. (4)
1.2.3 After the building of the room was completed, Ayryn needed to paint the inside walls. The painter indicated that two coats will be needed.
- The surface area of the room to be painted is 15 m2.
- 8% more paint will be needed.
- The spread rate is 5 m2per litre.
Calculate how many 5-litre tins must be bought. (4)
1.3
| The graph shown in ANNEXURE B shows the prediction of the South African average house prices forecast to 2020. Use the graph (ANNEXURE B) to answer the following questions. |
1.3.1 It is predicted that the price of an average house in South Africa increased by 5% in 2015 and by 4% thereafter to 2020.
Based on the above prediction determine the price of an average house for 2016. (4)
1.3.2 Calculate the percentage change in the price of an average house in South Africa for the period illustrated in the graph. Give your final answer to the nearest percentage. (4) [37]
QUESTION 2
2.1
| Gustav, a 52-year-old employee, married with 2 children, aged 10 and 16 years respectively, earns a gross annual salary of R401 137,75. He contributes 7,5% (non taxable) of his annual salary to a pension fund. He also contributed to a medical aid scheme for the whole family. Use the Tax Table for the 2018–2019 financial year in ANNEXURE C to answer the following questions. |
2.1.1 Calculate Gustav’s taxable income for the 2018–2019 financial year. (3)
2.1.2 For 11 months Gustav pays R2 500 per month for his 10-year-old and R3 200 per month for his 16-year-old in school fees.
He claims that with the tax he is paying for the year, he could have paid his children’s school fees. Show, with the necessary calculations, whether his
statement is valid or not. (9)
2.2
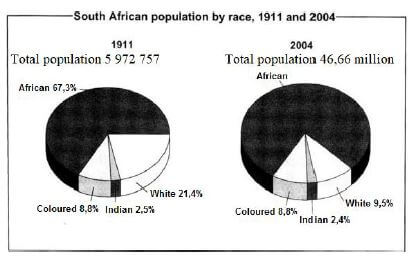
Sipho is teaching Social Sciences to Grade 9 learners at his school. He uses the pie charts below to show how the population percentages in South Africa changed according to the different race groups. The pie charts represent 1911 and 2004 respectively. Study the pie charts below to answer the questions below.
Source: http://reddit.com] |
2.2.1 Determine the probability of randomly choosing a person other than African from the 2004 population. (2)
2.2.2 Calculate the difference in the total number of the African population group between 1911 and 2004 in South Africa. (7)
2.2.3 The percentage of the Coloured population in 1911 and 2004 is the same. Show, with the necessary calculations, whether the number of Coloured
populations in these two years are the same. (3)
2.2.4 Comment on the trend and the percentages of African and Indian race groups over the period. (2)
2.3
| The Grade 12 class for 2019 has a farewell function to organise. Each learner must contribute R300,00. There are 25 couples and 17 singles. The organisers got two quotes as follow: Option 1: R1 500 for the hall and R250 per person for the meal Option 2: R270 per person for the singles and 4% less for couples per person |
2.3.1 Determine the total number of people that will attend the farewell. (2)
2.3.2 The organisers claim that if they choose Option 1 instead of Option 2, they can have more money left to spend on photos. Verify, with the necessary
calculations, whether the statement is valid or not. (8) [36]
QUESTION 3
3.1 Below is an extract of a map that show the location of two airports in Germany, Frankfurt-Hahn and Frankfurt airports. Study the map and answer the questions that follow.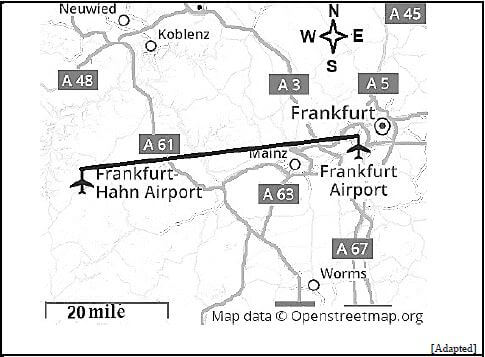
[Adapted]
3.1.1 In which general direction is Neuwied from Mainz? (2)
3.1.2 Calculate the actual distance in miles between the two airports. Give your final answer to THREE decimal places. (4)
3.1.3 Write the scale of the map as a unit ratio (1: …) to the nearest million.
You may use the following conversion:
1 mile = 1,609 kilometres (4)
3.1.4 Give ONE possible reason why airports in general are located away from residential areas. (2)
3.1.5 On which road on the western side will you travel from Worms to Koblenz? (2)
3.1.6 The travelling distance from Worms to Koblenz is 78 miles.
Judith claims that if she leaves Koblenz at 07:20 and travels at an average speed of 40 miles per hour, she will be on time for her interview at 09:15 in Worms. Show, with the necessary calculations, whether her claim is valid or not.
You may use the formula:
Distance = Speed × Time (7)
3.2
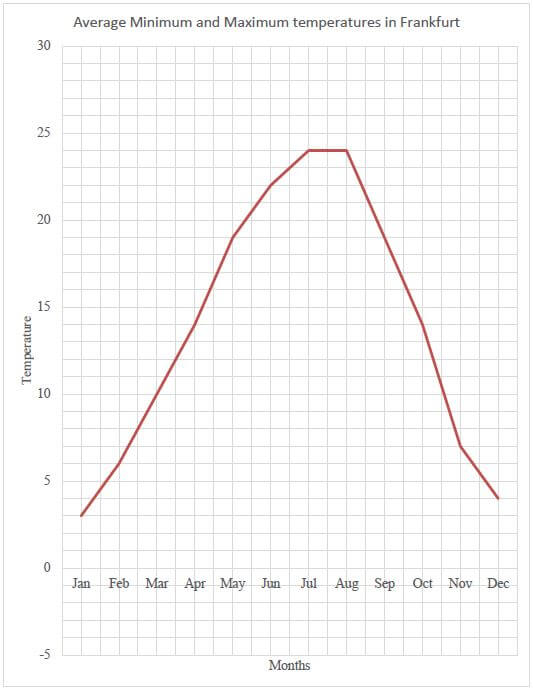
Kenneth plan to visit Judith in Frankfurt. Judith sent him the annual average minimum and maximum temperatures for Frankfurt as shown below.
[Adapted from http://lh-travelguide.com] |
Study the information above and answer the questions below.
3.2.1 The range of the data for the minimum temperature is 15 °C. Determine the lowest temperature indicated by A. (3)
3.2.2 Judith made two mistakes when calculating the median of the maximum temperatures. The following is her calculation:
Median = 22 + 24
2
= 34
- Identify Judith’s mistakes. (2)
- Calculate the median. (2)
3.2.3 Kenneth says he hates getting cold. Advise him with a reason which months he must visit Judith. (3)
3.2.4 Determine the probability that the minimum temperature will be greater than minus 1 °C, but less and equal to 9 °C. Give your final answer as a decimal fraction to THREE decimal places. (3)
3.2.5 The line graph for the maximum temperatures has been drawn in ANSWER SHEET 1. Use the same set of axes to draw the line graph for the minimum temperatures. (5) [39]
QUESTION 4
4.1
| Jona wants to build his own hot air balloon. He follows the illustrations as shown in ANNEXURE D. |
4.1.1 Diagram R is only a part of Diagram Q. Determine the total area of the material that the hot air balloon is made of.
You may use the following formulae:
Area of rectangle = Length × Width
Area of triangle = 1/2× base × height (8)
4.1.2 Give a reason why there must be an overlap of 3 mm on the sides as illustrated in Diagram T. (2)
4.1.3 Briefly explain what Jona has to do with the hot air balloon in Diagram T and Diagram U. (2)
4.1.4 Write down the function of the hair dryer in Diagram V. (2)
4.2
| Jona wants to have a ride in a hot air balloon. He did some research and came across an illustration shown in ANNEXURE E. It shows how hot air balloons are lifted depending on the temperature. |
4.2.1 Use ANNEXURE E to describe the relationship between the temperature of the hot air balloon and the lift of the hot air balloon. (4)
4.2.2 The table below shows the density of air at sea level for various temperatures of the hot air balloon.
Temperature in °C | Air density kg/m3 |
0 | 1,293 |
10 | 1,247 |
20 | 1,204 |
30 | 1,165 |
40 | 1,128 |
80 | 1,000 |
90 | 0,972 |
100 | 0,946 |
[Source: http://buoyancy.png]
With reference to the table above and ANNEXURE E to answer the following question.
Determine the lift of hot air balloon B.
You may use the following formula:
Lift = (Air density outside the hot water balloon – Air density inside hot air balloon) × Volume of the hot air balloon (7)
4.2.3 The instructor has hot air balloons with a variety of colours. Thirty-three green, eight orange, nineteen pink, twenty-one red and twelve blue. Determine the probability that Jona will choose either a green or a blue hot air balloon to ride in. Give your final answer as a common fraction in its simplest form. (3)
4.3
| Jona and three friends wants to visit Cappadocia, a historical region in Central Anatolia in Turkey where they will also go for the hot air balloon rides. They investigated the cost of their accommodation and the cost of the hot air balloon rides to get an idea of the costs. They received the following information: Accommodation: R1 030 per person per night Hot air balloon rides: R750 per person per ride NOTE: They are checking in on Monday (15 April 2019) and checking out on Friday (19 April 2019). Group bookings for the hot air balloon rides for 4 persons will be charged at a discount of 15% per person. |
Use the information above to calculate how much Jona and his friends will pay in total for the accommodation and one hot air balloon ride, if they go as a group. Give your final answer in Turkish Lira.
Exchange rates as at 08 February 2019:
| 1$ (American Dollar) = 5,25 Turkish Lira 1$ (American Dollar) = 13,63 ZAR (South African Rand) |
[Source: http://ferates.com] (10)
[38]
TOTAL: 150
ANSWER SHEET 1: QUESTION 3.2.5
NAME and SURNAME: …………………………………………………………………. Grade 12: …………..