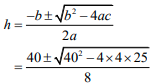TECHNICAL MATHEMATICS PAPER 2 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2020 PREPARATORY EXAMINATIONS

NATIONAL SENIOR CERTIFICATE
GRADE 12
SEPTEMBER 2020
TECHNICAL MATHEMATICS P2
MARKING GUIDELINE

NOTE:

Continuous accuracy (CA) applies only where indicated in this marking guideline.
Assuming values/answers in order to solve a problem is unacceptable.

MARKING CODES
M	Method
A	Accuracy
AO	Answer Only
CA	Consistent Accuracy
F	Formula
I	Identity
R	Rounding
S	Simplification
ST	Statement
RE	Reason
ST RE	Statement and correct reason
SF	Substitution correctly in correct formula
NPU	No penalty for omitting units

QUESTION 1


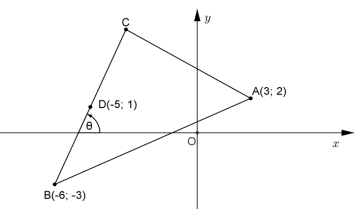1.1	AB = √((x₂ − x₁)² + (y₂ − y₁)²) =√((3 + 6)² +( 2+ 3)²) = √((−6−3)² + (−3− 2)²) = √106	✓ SF A ✓ CA	(2)
1.2.1	m_BC = m_BD = = 1 + 3 = −3−1 −5 +6 −6+5 =4	✓SF A ✓gradient	(2)
1.2.2	tan θ = m_BC = 4 ∴ θ = tan⁻¹ (4) ∴ θ ≈ 76°	✓ M ✓CA Rounded answer	( 2)
1.2.3	∴ x_c − 6 = −10 y_c = −3 = 2 ∴ x_c = −4 y_c = 5	✓M ✓S ✓S ✓CA Both answers
1.2.4	m_{new line} = 4 y − y₁ = m(x − x₁) ∴ y − 2 - 4(x−3) ∴y − 2 = 4x −12 ∴y = 4x − 10 OR m_{new line} y = mx + c 2 = − 4(−3) +d c = −10 Y = 4x − 10	✓ CA gradient of new line ✓SF CA gradient and point A ✓S ✓CA OR ✓ CA gradient of new line ✓SF CA gradient and point A ✓S ✓CA	(3)
			[13]

QUESTION 2


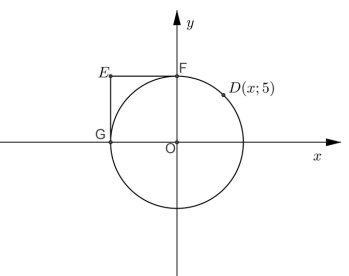2.1.1	x² + y² = 49 ∴ x² + 25 = 49 ∴ x² = 24 ∴ x = √24 = 2√6	✓SF A ✓ S CA ✓ CA surd form	(3)
2.1.2 (a)	EF : y = 7 EG : x = −7	✓A y ✓A 7 ✓A x ✓A −7	(4)
2.1.2 (b)	E(−7; 7)	✓CA	(1)
2.2.1	16x² + 49y² = 784 x² + y² = 1 49 16	✓A LHS ✓A RHS	(2)
2.2.2		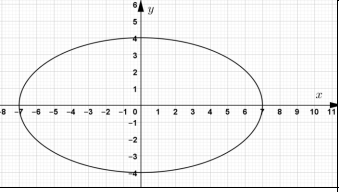✓CA x-intercepts ✓CA y-intercepts ✓CA elliptical shape	(3)
			[13]

QUESTION 3

3.1.1	cosec A − tan B = cosec 123° − tan 65° = 1 − tan 65° sin123° ≈ − 0,95	✓A 1 sin 123° ✓ A −0,95 AO: Full marks	(2)
3.1.2	cot² (A + 2B) = 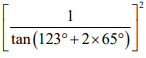≈ 0,09	✓ A 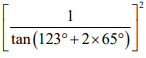✓ A 0,09 AO: Full marks	(2)
3.2	sin ^π/₆ + sec² ^π/₄ = sin 30° + 1 cos² 45° = 0,5 + 2 =2,5	✓ A 0,5 ✓A 2 ✓ CA 2,5 AO : Full marks	(3)
3.3	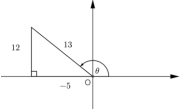cot θ − sec θ = ⁻⁵/₁₂ − ¹³/₋₅ = ¹³¹/₆₀ ≈2,18	✓A diagram in correct quadrant ✓A values of sides ✓ CA cot θ = ⁻⁵/₁₂ ✓CA sec θ = ¹³/₋₅ ✓2,18	(5)
3.4	(tan²θ + 1)(1−cos²θ) =sec²θ × sin²θ = 1 × sin²θ cos²θ =tan²θ	✓A sec²θ ✓A sin²θ ✓A 1 cos²θ ✓A tan²θ	(4)
3.5	sin (180° + x).tan135° sec(180° − x) .cos (360° − x) = (−sin x)(−1) (−sec x )(cos x) = sin x −1 = − sin x	✓A sin x ✓ A −1 ✓ A −sec x ✓ A cos x ✓ A −1 ✓ CA −sin x	(6)
			[22]

QUESTION 4


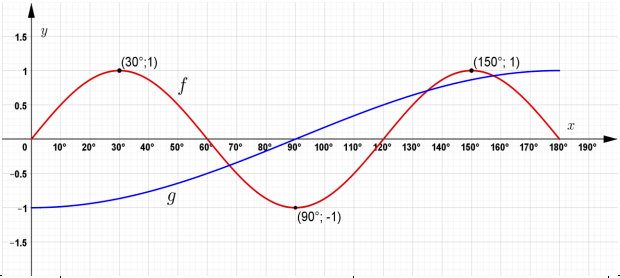4.1		f: ✓A x-intercept ✓A turning points ✓A shape ✓A start and end point ✓A x-intercept	(5)
4.2	120° OR period = 360°= 120° 3	✓ A	(1)
4.2.2(a)	90° ≤ x ≤ 180°	✓CA interval ✓ CA notation	(2)
4.2.2(b)	0° ≤ x ≤ 60° OR 90° ≤ x ≤ 120°	✓ CA interval 1 ✓ CA notation ✓ CA interval 2 ✓ CA notation	(4)
4.2.2(c)	x = 90° and x = 180°	✓CA 90° ✓CA 180°	(2)
			[14]

QUESTION 5


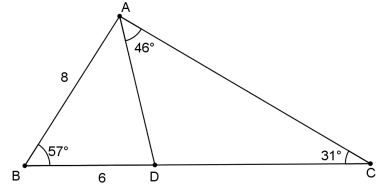5.1	Area Δ ABD = ½ad sin B =½ × 6 × 8 sin 57° =20,13 sq units	✓ F ✓ SF ✓CA	(3)
5.2	AD² = AB² + BD² − 2AB.BDcosB =8² + 6² − 2 × 8 × 6 cos 57° =47,714... AD ≈ 6,91 units	✓F ✓SF A ✓CA ✓R	(4)
5.3	CD = AD sin CAD sin C CD = 6,91 sin 46° sin 31° CD = 6,91 sin 46° sin 31° ≈ 9,65 units	✓F ✓SF A ✓S CA ✓CA	(4)
			[11]

QUESTION 6

6.1	Bisect the chord	✓ A	(1)
6.2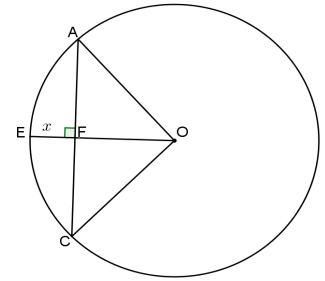
6.2.1	AO = x + 7	✓A	(1)
6.2.2	AF = 24 units (line from centre ⊥ to chord0 AO² = AF² + OF² (pyth) ∴ (x+7)² = 24² + 7² ∴ x² + 14x + 49 = 625 ∴ x² + 14x − 576 = 0 ∴ (x+32)(x−18) = 0 ∴ x≠ −32 or x = 18	✓ST ✓RE ✓M ✓ST CA ✓ST CA	(5)
6.3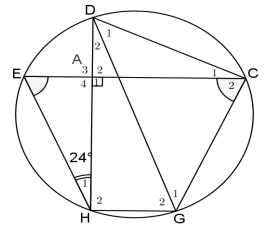
6.3.1	E = 66° (Int ∠s of Δ ∴ C₂ = 66° (given) D = 66° ( ∠s in same seg	✓ST RE ✓ST ✓ST ✓RE	(4)
6.3.2	HGC = 114° (opp ∠s of cyclic quad)	✓ST ✓ RE	(2)
6.3.3	C₁ = 24° ( ∠s in same seg) ∴ C = 90° ∴ DG is a diameter (chord subtends 90°) OR ∴DG is a diameter ( converse ∠ in semi-circle	✓ST ✓ RE ✓RE	(3)
			[16]

QUESTION 7

7.1	tangent to the circle	✓A	(1)
7.2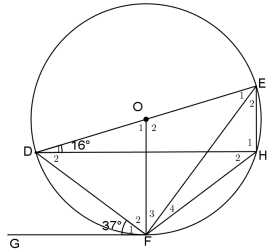
7.2.1	H₂ = 37° (tan-chord)	✓ST ✓ RE	(2)
7.2.2	F₂ = 53° rad ⊥ tangent)	✓ST ✓ RE	(2)
7.2.3	D = 53° (∠ opp equal sides: DO and FO radii O₂ = 106° (ext ∠ of Δ) OR D = 53° (∠ opp equal sides: DO and FO radii O₂ = 106° (∠ at centre = 2 × ∠ at circumference)	✓ST ✓ RE ✓ST ✓ RE OR ✓ST ✓ RE ✓ST ✓ RE	(2)
7.2.4	E₂ = D₂ (∠ s in same segm.) E₂ = 53°−16° = 37°	✓ST ✓ RE ✓ST	(3)
			[10]

QUESTION 8

8.1	Parallel	✓A	(1)
8.2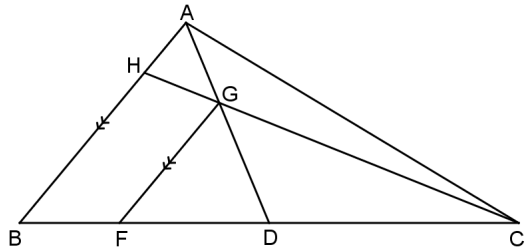
8.2.1	BF = AG (line II to one side of Δ) FD GD =½	✓ST ✓ RE ✓ST	(3)
8.2.2	CG = CF (line II to one side of Δ) CH CB CF = CD + DF CB CD + DB = 3 + 2 (D midpoint) 3 + 3 CG = 5 CH 6	✓ST ✓ RE ✓ST ✓ST	(3)
8.3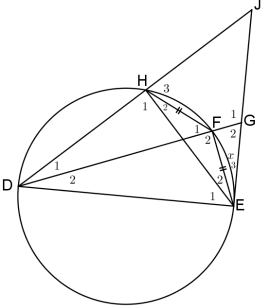
8.3.1	D₂ = x (tan-chord) H₂ = x (∠s in same seg) E₂ = x (∠s opp equal sides) OR D₂ = x (tan-chord) H₂ = x tan-chord) E₂ = x (∠s opp equal sides)	✓ST ✓ RE ✓ST ✓ RE ✓ST ✓ RE OR ✓ST ✓ RE ✓ST ✓ RE ✓ST ✓ RE	(5)
8.3.2	In ΔDFE and Δ DEG: D₂ (common) F₂ = 90° ( ∠ in semi-circle) E = 90° (tan ⊥ radius ∴ ΔDFE///ΔDEG (AAA)	✓ST ✓ RE ✓ST ✓ RE ✓ST ✓ RE ✓ RE	(6)
			[18]

QUESTION 9


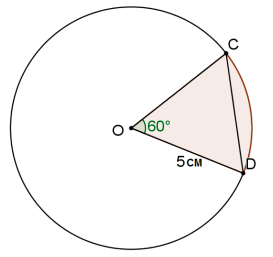9.1	s = rθ = (5) (60° × ^π/_180° =^5π/₃ ≈ 5,24cm	✓F ✓ SF A × ^π/_180° ✓M ✓CA	(4)
9.2	Area of sector = ^rs/₂ Opp van sektor = = ²⁵/₆ π ≈13cm² OR Area of sector = r²θ 2 Opp van sektor = = ²⁵/₆ π ≈13cm²	✓F ✓ SF A ✓CA ✓R OR ✓F ✓ SF A ✓CA ✓R	(4)
9.3(a)	OCD = ODC (∠s opp = sides CD = 5cm (equiangularΔ)	✓ST ✓ST AO: Full marks	(2)
9.3(b)	4h² − 4dh + x² = 0 4h² − 4(10)h+(5)² = 0 4h² − 40h + 25 = 0 = 40 ± √ 1200 8 =0,67 or 9,33 ∴ required height = 0,67cm	✓F ✓ SF A ✓ S CA ✓ CA ✓C	(5)
			[15]

QUESTION 10

10.1.1	180rpm = 180 rev × 1 min = 3 rps 1 min 60 sec	✓ conversion ✓ SA AO: Full marks	(2)
10.1.2	n = 3rps v = πDn r = 6 ⇒ d = 12 v = π × 12 × 3 = 36πcm/s	✓F ✓SF A ✓CA	(3)
10.1.3	w = ^v/_r = ^36π/₆ = 6π rad/s	✓F ✓SF A ✓CA	(3)
10.2	V_cylinder = πr²h 1l = π(12cm)²h 1000cm³ = 144πh cm² h = 2,2 cm	✓F ✓ A 1l = 1000 cm³ ✓SF A ✓CA	(4)
			[12]

QUESTION 11

11.1	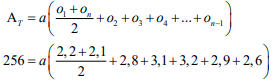= 16,75a a = 15,28 OR = 16,75a a = 15,28	✓F ✓SF A ✓CA ✓ value of a OR ✓F ✓SF A ✓CA ✓ value of a	(4)
11.2	Length of straight edge = 15,28 × 6 = 91,68m	✓M ✓ CA	(2)
			[6]
	TOTAL		150

Last modified on Friday, 18 February 2022 07:24