INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of 10 questions.
2. Answer ALL the questions.
3. Clearly show ALL calculations, diagrams, graphs, et cetera, that you have used in determining your answers.
4. You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
5. If necessary, ALL answers should be rounded off to TWO decimal places, unless stated otherwise.
6. Number the answers correctly according to the numbering system used in this question paper.
7. Diagrams are NOT necessarily drawn to scale.
8. An information sheet with formulae is attached.
9. Diagram sheets are attached for QUESTION 3.4 and QUESTION 8.1.5. Write your name in the spaces provided and hand in the diagram sheets with your ANSWER BOOK.
10. Write neatly and legibly.

QUESTIONS

QUESTION 1
1.1 Solve for x:
1.1.1 x (x − 5) = 6  (4)
1.1.2 -2x² - 4x - 1 = 0   (correct to ONE decimal place) (3)
1.1.3     , also represent the solution on a number line.(4)
1.2 Diagram A below shows a ticker timer, tape and a trolley.
Diagram B shows the top view of the tape with the results recorded by the ticker timer on the tape, as dots.
Diagram A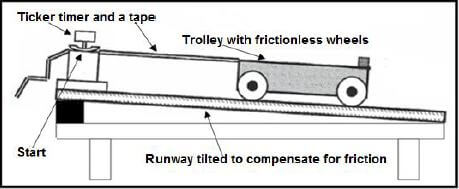

Diagram B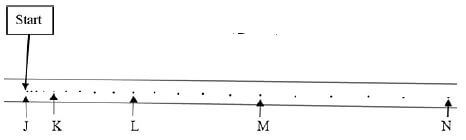

• Each dot on the tape corresponds to ONE second lapse by the timer.
• 5 dot intervals are indicated by points K, L, M and N from start position, J, in Diagram B.

1.2.1 How many seconds were recorded by the timer on the tape from J to N? (1)
1.2.2 Convert the time from J to N into hours. (1)
1.2.3 Hence, express the hours in QUESTION 1.2.2 in scientific notation. (1)
1.3 Solve the following equations simultaneously:

x = 2  and x² + xy + y = 2 (6)
y

1.4 Given: 2x² + bx + c = 0

1.4.1 If a = ¹/₂b and b= ¹/₂c calculate and evaluate the values of b and c. (2) 
1.4.2 Hence, without solving the equation, describe the nature of roots of 2x² + bx + c = 0 (2)

1.5 Write 41 as a binary number. (2) [26]

QUESTION 2
2.1 Simplify the following WITHOUT using a calculator:

2.1.1   (4)
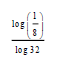2.1.2  (3)

2.2 Given: x = √2 and y = √3
Determine, without using a calculator, the numerical value of 2(x - y)(x + y) (3)
2.3 Solve for x if:  (8)
2.4 Solve for x and y if  3x - 5yi = -3 (3)
2.5 Write z =√3 - 2i in the form r (cos θ + isin θ)   (6) [27]

QUESTION 3
Given: ƒ(x) = 3^x - 4
3.1 Write down the equation of the asymptote of ƒ. (1)
3.2 Determine the x-intercept of ƒ. (3)
3.3 Determine the y-intercept of ƒ. (2)
3.4 Sketch the graph of ƒ on the ANSWER SHEET provided. Clearly show all the asymptotes and intercepts with the axes. (3)
3.5 Write down the range of ƒ. (1) [10]

QUESTION 4
In the diagram drawn below, is a linear function defined by f (x) = x + 2 and a semi-circle defined by g(x) = √r² - x²
ƒ and g intersect at point A and B respectively.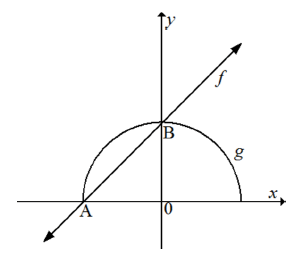

Determine:
4.1 The coordinates of point B (1)
4.2 The equation of the semi-circle, g (2)
4.3 The domain of g (2)
4.4 The value(s) of x for which ƒ(x) < g(x) and ƒ(x) >0 (2) [7]

QUESTION 5
The diagram below shows sketch graphs of functions defined by m(x) = ^p/_x + q ; x # 0 and h(x) = -x² + 4x - 3
A and B (1; − 1) are points on m(x) and h(x) cut the y-axis at C.

5.1 Determine the coordinates of C, the y-intercept of h. (2)
5.2 Determine the value of p. (2)
5.3 Write down the equation of m(x) (1)
5.4 Determine the coordinates of D, the turning point of h. (4)
5.5 Calculate the length of DE. (2) [11]

QUESTION 6
6.1 Determine the effective interest rate, compounded monthly, if the nominal interest rate is 6,2% per annum. (3)
6.2 A milling machine loses its value on a straight-line depreciation to R40 000 after 3 years. If the depreciation rate is 10% p.a., determine the original cost price of the machine. (4)
6.3 Water Drilling Project invested R280 000 for 10 years in an account to buy cash a borehole drilling machine, as shown in the picture below.

• The investment accumulates interest rate of 10% per annum, compounded half yearly for the first 6 years of the investment.
• After 6 years the company withdrew R150 000 from the investment account.
• The interest rate decreased from 10% to 7% per annum compound interest for the remaining 4 years of investment.
• The cost price of the borehole drilling machine is expected to be approximately R450 000 after 10 years.
  Calculate how much money will be in the investment account after 10 years. (6) [13]

QUESTION 7
7.1 Determine the derivative of f(x) = -2x + 2 by using first principles. (5)
7.2 Evaluate: 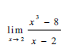    (3)
7.3 Determine:

7.3.1   (4)
7.3.2    (3)       [15]

QUESTION 8
8.1 G iven : f(x) = (1 - 2x)(x² - 4)   

8.1.1 Write down the y-intercept of ƒ. (1)
8.1.2 Determine the x-intercepts of ƒ. (3)
8.1.3 Write ƒ(x) in the form of ƒ(x) = ax³ + bx² + cx + d (1)
8.1.4 One of the turning points of ƒ is (−1;−9). Determine the coordinates of the other turning point of ƒ. (5)
8.1.5 On the ANSWER SHEET provided, sketch the graph of f. Clearly show all the coordinates of the turning points and intercepts with the axis. (4)

8.2 Determine the value(s) of a, if the average gradient of g(x) = 2x² - x - 3 between x = a and x = 4 is 9.  (5)    [19]

QUESTION 9
The driver of a motor car fills the petrol tank of his car to full capacity in a petrol station, to undertake a journey that requires a minimum of 25 ℓ of fuel to drive.
Unfortunately, he knocks his car on the corner of the road pavement as he leaves the petrol station resulting into a leakage from an opening in his petrol tank.
The picture below shows the damaged petrol tank of the car.

The equation, V(t) = t² - 9t + 35 represents the amount of petrol lost over time (t) in minutes.
Determine:
9.1 The amount of petrol in the tank before the leakage (2)
9.2 The amount of petrol that leaked out after 1 minute (2)
9.3 The time it took for maximum petrol to leak out of the tank (3)
9.4 The maximum amount of petrol that leaked (2) [9]

QUESTION 10
10.1 Determine the integral:

10.2 The graph of ƒ and g defined by ƒ(x) = -x + 4 and g(x) = ²/_x respectively, intersect at x = 0,59 and x = 3,41, as shown in the diagram below.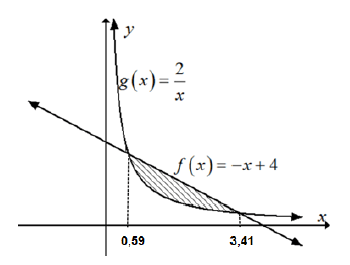

10.2.1 Determine the area bounded by the graph of ƒ(x) = -x + 4 and the x-axis, between x = 0,59 and x = 3,41. (6)
10.2.2 If it is given that the area bounded by the graph of g and the x-axis between x = 0,59 and x = 3,41 is equal to 3,51 square units, calculate the striped area between the graphs of ƒ and g. (3)
[13]
TOTAL: 150

INFORMATION SHEET: TECHNICAL MATHEMATICS

ANSWER SHEETS

NAME: ............................................................
SCHOOL: ............................................................
QUESTION 3.4

ANSWER SHEET

NAME:
SCHOOL:
QUESTION 8.1.5