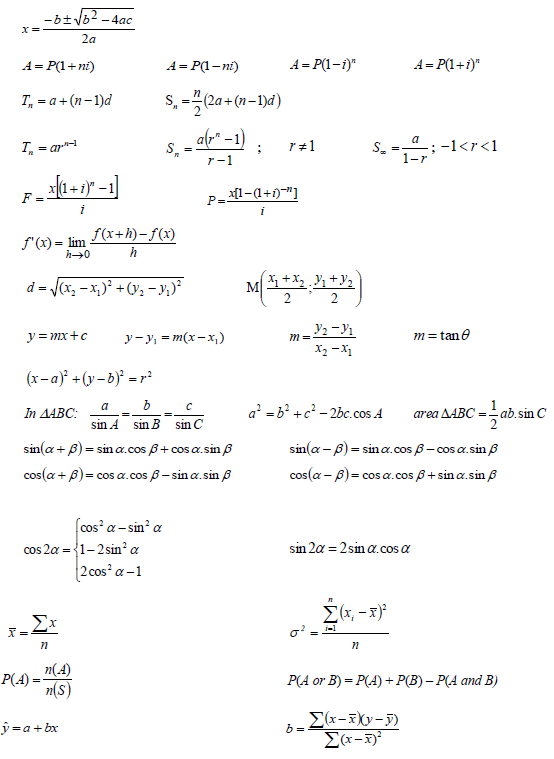Mathematics P1 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupINSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of ELEVEN questions. Answer ALL the questions.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answer.
- You may use an approved scientific calculator (non-programmable and non graphical), unless stated otherwise.
- Answers only will NOT necessarily be awarded full marks.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- Number the answers correctly according to the numbering system used in this question paper.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 x2 - 3x − 4 = 0 (3)
1.1.2 2x2 − x − 7 = 0 (correct to TWO decimal places) (3)
1.1.3 5x+1 − 5x = 2500 (3)
1.1.4 (x − 3)(x + 1) < 12 (4)
1.2 Solve the following equations simultaneously:
2x = y + 1
3x2 − xy − y2 = 1 (6)
1.3 Given that ƒ(x) = x2 − 2px + 8 + 2p has two equal roots and p < 0, determine the coordinates of the turning point of h, if h(x) = f (x) – 3. (5) [24]
QUESTION 2
2.1 Given the quadratic number pattern: 3 ; 1 ; −3 ; −9 ; …
2.1.1 Write down the next 2 terms of the pattern. (1)
2.1.2 Determine Tn, the ntℎ term of the pattern, in the form Tn = an2 + bn + c. (4)
2.1.3 Which term of the pattern has a value of −809? (3)
2.2 Given the arithmetic sequence: −1 ; 1 ; 3 ; 5 ; …
2.2.1 Determine T53, the 53rd term of the sequence. (2)
2.2.2 Determine the sum of the first 29 terms of the sequence. (2)
2.2.3 Hence, write your answer in sigma notation. (2)
2.3 In an arithmetic sequence, T4 = 2x + y and T10 = 8x − 2y. Determine the first term of the sequence in terms of x and y. (5) [19]
QUESTION 3
Given that: 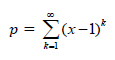
3.1 Determine the values of x for which p converges. (2)
3.2 Calculate the value of p when x = 2/3 (4) [6]
QUESTION 4
Given: ![]()
4.1 Write down the equations of the asymptotes of ƒ. (2)
4.2 Calculate the x and y intercepts of ƒ. (3)
4.3 Draw a neat sketch of ƒ, clearly indicating all intercepts with the axes and any asymptotes. (4)
4.4 Given that h is a reflection of f in the x-axis, determine the equation of the axis of symmetry of h having a positive gradient. (4) [13]
QUESTION 5
The diagram below shows the graphs of ƒ(x) = x2 − 7x − 8 and g(x) = mx + c. P and R are x-intercepts of ƒ, and V is the x-intercept of g. S is the turning point of ƒ. ƒ and g intersect on the y-axis at Q and also at T(9; 10).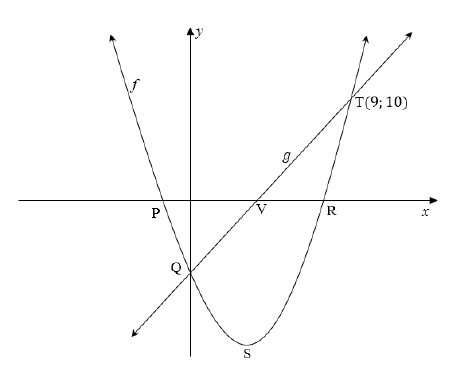
5.1 Write down the coordinates of Q. (1)
5.2 Determine the equation of g. (3)
5.3 Write down the equation of f in the form y = a(x + p)2 + q. (2)
5.4 Hence, or otherwise, determine the coordinates of S, the turning point of f. (2)
5.5 Determine the coordinates of a point W, on f , such that the average gradient between T and W is 1. (5)
5.6 Determine the values of x for which ƒ(x). g(x) < 0. (4) [17]
QUESTION 6
Given: ƒ(x) = logmx
6.1 Determine the value of m, if the point (64;3)lies on ƒ. (2)
6.2 Determine the equation of ƒ−1 in the form y =… (2)
6.3 Draw a neat sketch of ƒ−1, showing all intercepts with the axes. Indicate at least one other point on your graph. (2)
6.4 Write down the range of h if: ℎ(x) = ƒ−1(x) − 2 (1) [7]
QUESTION 7
7.1 Kamva bought a motorbike valued at R40 000. After 5 years the value of the motorbike had depreciated to R26 700, at a rate of r % p.a. on the reducing balance method, compounded annually. Calculate r, the rate of depreciation. (3)
7.2 A bank granted Nathan a loan for R1 200 000 to buy a house. He agreed to repay the loan over a period of 15 years at an interest rate of 11,5% p.a. compounded monthly. He made his first payment at the end of the first month after the loan was granted.
7.2.1 Calculate Nathan’s monthly instalment. (3)
7.2.2 Due to unforeseen circumstances, Nathan could not pay his 76th, 77th, 78th, 79th and 80th instalments. He resumed his payments at the end of the 81st month.
- Calculate the outstanding balance at the end of the 80th month. (5)
- If Nathan continues paying the same monthly instalment, how many months will it take him to pay the balance outstanding at the end of the 80th month? (4) [15]
QUESTION 8
8.1 Determine ƒ′(x) from first principles if ƒ(x) = 3 − 2x2(5)
8.2 Determine:
8.2.1 ![]() (4)
(4)
8.2.2 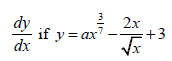 (3) [12]
(3) [12]
QUESTION 9
The diagram below shows the graph of y = g′(x) where g(x) = ax3 + bx2 + cx + d. The graph g′(x) cuts the y-axis at (0; 1) and the x-axis at (−13; 0) and (1; 0).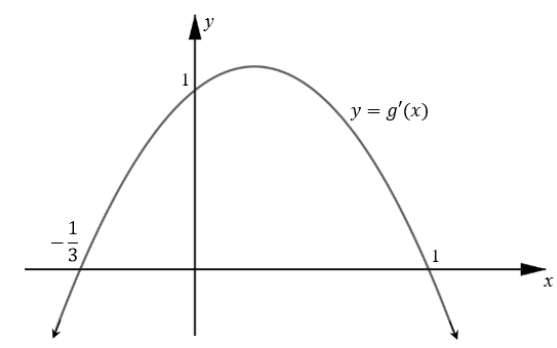
9.1 Write down the x-coordinate(s) of the stationary point(s) of g. (2)
9.2 Determine the x-coordinate of the point of inflection of g. (2)
9.3 Determine the values of x for which g is an increasing function. (2)
9.4 Determine the equation of g′(x) in the form: g′(x) = px2 + qx + r. (4)
9.5 Given that:
- g(x) + 1 passes through (0;0)and
- g′(x) = −3x2 + 2x + 1
Show that for g(x), a = −1, b = 1, c = 1 and d = −1. (5) [15]
QUESTION 10
Two numbers are such that their sum is 18. One of the numbers is multiplied by the square of the other. Calculate the numbers that make this product a maximum. [7]
QUESTION 11
11.1 A school has 530 learners. Each learner is expected to choose his/her summer extra-curricular activity from the following:
- Athletics
- Cricket
- Tennis
The choices for 2019 were recorded in the following partially completed table:
| Athletics | Cricket | Tennis | Total | |
| Girls | 120 | a | 57 | 288 |
| Boys | b | 108 | 28 | 242 |
| Total | 226 | 219 | 85 | 530 |
11.1.1 Determine the values of a and b. (2)
11.1.2 A learner is chosen at random. Determine the probability that:
- It is a boy who plays cricket (2)
- It is a girl or not a tennis player (3)
11.2 Consider the letters of the word: NUMERATOR.
11.2.1 How many 9 letter word-arrangements can be formed, if repetition of letters is allowed? (1)
11.2.2 How many 9 letter word-arrangements can be formed, if all 4 vowels are never together and repetition of letters is not allowed? (3)
11.2.3 An 8 letter word-arrangement is made from the word NUMERATOR. All the vowels must be included in this word-arrangement and repetition of letters is not allowed. What is the probability that all odd-number spaces are occupied by vowels? (4) [15]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS