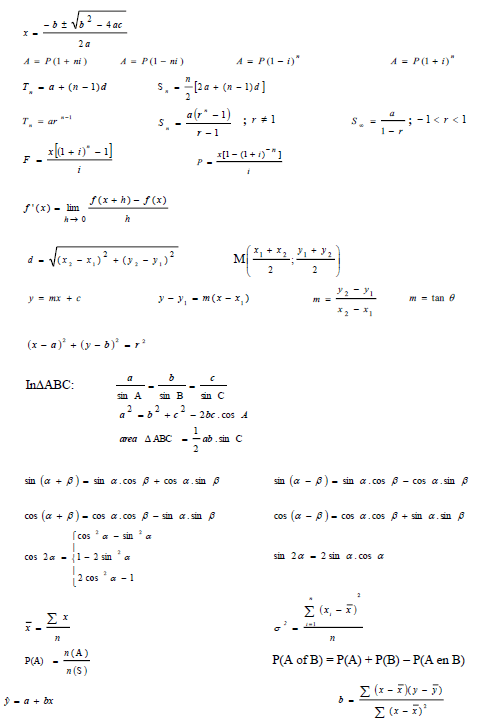Mathematics P2 Grade 12 Questions - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupINSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
The table below shows the height, in metres, of 80 giraffes.
1.1 Calculate the estimated mean height of the giraffes. (2)
1.2 The height range of 4,8 ≤ ℎ < 5,0 m, consisted entirely of 7 young male giraffes. The mean of the heights of the 7 young males was calculated to be 4,86 m. However, it was noticed that the height of one of the young males was incorrectly recorded as 4,98 m but should have been 4,89 m. Calculate the new mean of the 7 young males. (3)
1.3 Would you expect the standard deviation of the individual heights of the 80 giraffes to be more or less than the standard deviation of the individual heights of the 7 young male giraffes? Explain your answer. (2) [7]
QUESTION 2
| Cocoa solids are used to make chocolate. A student is investigating the relationship between the percentage of cocoa solids in a 100g slab of chocolate and the price of the slab (in rands). The data obtained is shown in the table below. |  |
| chocolate brand | A | B | C | D | E | F | G | H |
| x (% of cocoa) | 10 | 20 | 30 | 35 | 40 | 50 | 60 | 70 |
| y (price in rand) | 6,50 | 10,20 | 9,40 | 24,00 | 11,20 | 16,80 | 20,50 | 24,20 |
2.1 Use the grid in the ANSWER BOOK to represent this data in a scatter plot. (2)
2.2 Determine the equation of the least squares regression line for this data. (3)
2.3 Draw the least squares regression line in the ANSWER BOOK on the same grid used in QUESTION 2.1. (2)
2.4 Calculate the correlation coefficient for the percentage of cocoa solids and the price of the chocolate slab. (1)
2.5 Comment on the relationship between the percentage of cocoa solids and the price of the chocolate slab. (1)
2.6 The student believes one brand of chocolate is overpriced.
2.6.1 Identify the chocolate brand which is over-priced. (1)
2.6.2 Estimate by how much more this slab of chocolate is overpriced. (3) [13]
QUESTION 3
In the diagram below, ∆ABC is shown with coordinates of A (4; – 3) and B (4 ; 6) given. AB intersects the x-axis at D and AC intersects the y-axis at E.
The coordinates of E are ![]() . BC intersects the y-axis at R. P is a point on the y-axis.
. BC intersects the y-axis at R. P is a point on the y-axis.
DE ∥ BC.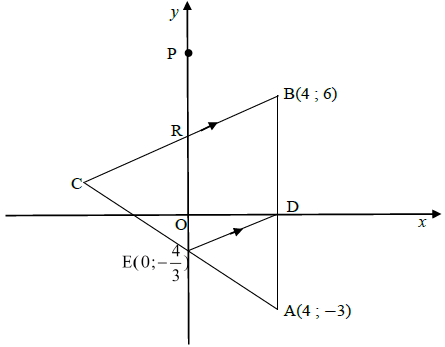
3.1 Write down the coordinates of D. (1)
3.2 Determine the gradient of DE. (2)
3.3 Calculate PR̂B. (4)
3.4 Calculate the length of DE in simplest surd form. (2)
3.5 Determine the ratio AD: AB in its simplest form. (2)
3.6 Hence, or otherwise, calculate the length of BC. (3)
3.7 Determine:
3.7.1 The midpoint of DE (2)
3.7.2 The equation of the perpendicular bisector of DE in the form y = mx + c (3)
3.8 Does this perpendicular bisector pass through A? Justify your answer. (2) [21]
QUESTION 4
The diagram below shows a circle having centre M which intersects the x-axis at A and B and the y-axis at D and C. PCQ is a tangent to the circle at C, the point of contact on the y-axis. P lies on the x-axis.
The equation of the circle is: x2 + y2– 6x – 16 = 0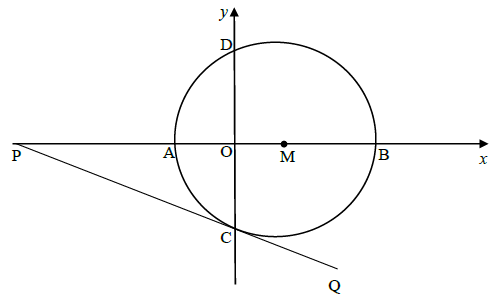
4.1 Show that the coordinates of M are (3; 0) and that the radius is 5 units. (3)
4.2 Determine:
4.2.1 The coordinates of B (3)
4.2.2 The coordinates of C (2)
4.3 If the length of PM is 81/3 units, calculate the length of PC. (3)
4.4 Calculate the angle subtended by the chord DC at B, i.e. find DB̂C. (4)
4.5 If the given circle is moved 2 units right and 1 unit up, determine the equation of the tangent to the circle in its new position passing through point C'. (4) [19]
QUESTION 5
DO NOT USE A CALCULATOR FOR THIS QUESTION.
5.1 Complete the following identities:
5.1.1 cos 2 A + sin 2 A = … (1)
5.1.2 cos 2 A − sin 2 A = … (1)
5.2 P(2 ; k) is a point in the Cartesian plane such that OP = 3 units and reflex angle TÔP = θ, as shown in the diagram below,
5.2.1 Calculate the value of k (leave your answer in surd form). (2)
5.2.2 Hence, determine the value of the following:
- tan (θ – 180º) (2)
 (4)
(4)
5.3 Determine, without the use of a calculator, the value of:
sin (−200º).cos 310º + tan (−135º).cos 380º.sin 230º (6)
5.4 Prove the following identity:
sin 2θ + cos (2θ – 90º) = 4 sin θ cos θ (3)
5.5 Solve for x if:
10 sin x + 10 sin x + 1 = 110 for − 360º ≤ x ≤ 360º (5) [24]
QUESTION 6
The graph below shows part of the function f (x) = sin 2x for 0º ≤ x ≤ 180º.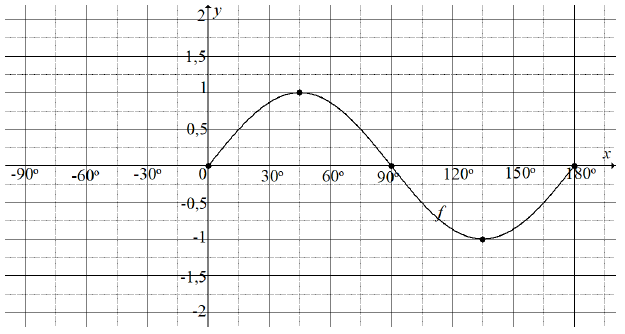
6.1 On the grid provided in the ANSWER BOOK, complete the graph of f for the interval − 90º ≤ x ≤ 180º. (1)
6.2 On the same grid, draw the graph of g (x) = cos (x – 30º) for the interval − 90º ≤ x ≤ 180º. Clearly show the intercepts with the axes, the coordinates of the turning points and the end points of the graph. (4)
6.3 Calculate the solutions to the equation:
sin 2x = cos (x – 30º) for – 90º ≤ x ≤ 90º(6) [11]
QUESTION 7
The diagram below shows a vertical netball pole PB. Player A is standing on the base line of the court and the angle of elevation from A to the top of the pole P is yº. A second player is standing in the court at C, and the angle of elevation from C to P is xº. Points A, B and C are in the same horizontal plane. BA is k metres; AB̂C = 100º.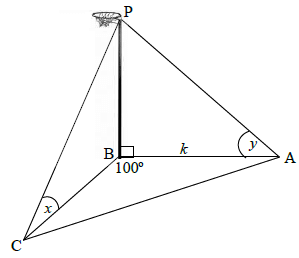
7.1 Show that BC = k.tan y (3)
tan x
7.2 Calculate the length of AC if BC = 4,73 m and k = 3 m. (3) [6]
Give reasons for your statements in QUESTIONS 8, 9, and 10.
QUESTION 8
8.1 In the given diagram, A, B, C, D and E are points on the circle.
BE is a diameter. Ê3 = 62º and B̂1 = 50º.
BD produced meets AE produced at F.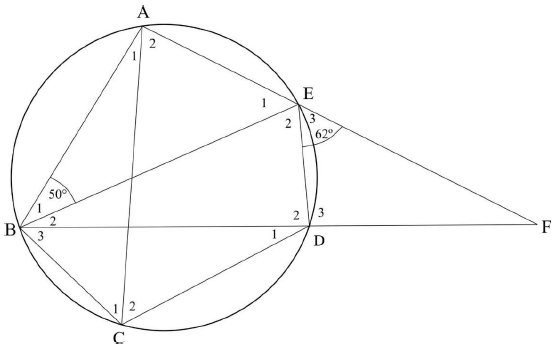
Determine, with reasons:
8.1.1 BÂE (2)
8.1.2 Ê1(2)
8.1.3 Ĉ1(2)
8.1.4 Ĉ2(2)
8.1.5 AB̂D (2)
8.2 Complete the following theorem statement: The angle between the tangent to a circle and the chord drawn from the point of contact is … (1)
8.3 In the diagram below, PRQ is a tangent to the circle SUR at R. SU, SR and UR are drawn. Lines from S and U produced meet at T outside the circle.
R̂1 = x ; Ŝ2 = y and ST̂U = x + y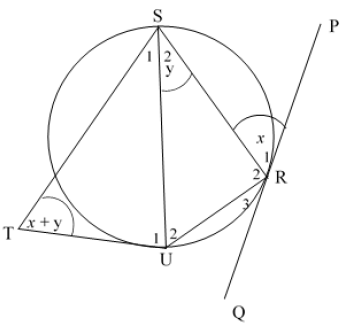
Prove that STUR is a cyclic quadrilateral. (5)
8.4 The diagram below shows a circle centre M passing through the points R, P, Q and T. RT is the diameter. PQ is a chord such that PQ ∥ RT and MN ⊥ PQ.
PQ = 16 units, MN = 6 units.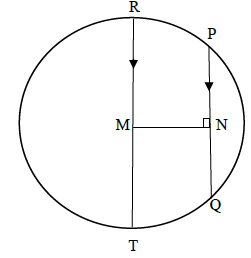
Determine the length of RT. (4) [20]
QUESTION 9
In the diagram below, ABCD is a parallelogram. AD and AC are produced to E and F respectively so that EF ∥ DC. AF and DB intersect at O.
AD = 12 units; DE = 3 units; DC = 14 units; CF = 5 units.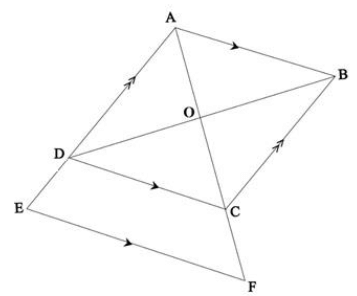
9.1 Calculate, giving reasons, the length of:
9.1.1 AC (3)
9.1.2 AO (1)
9.1.3 EF (3)
9.2 Prove that area  (3) [10]
(3) [10]
QUESTION 10
10.1 For the triangles shown below,
prove that if P̂ = Ŝ and Q̂ = T̂ and R̂ = Û then
ST = SU (6)
PQ PR
10.2 In the diagram below, O is the centre of a semi-circle ACB. S is a point on the circumference and T lies on AC such that STO ⊥ AB. Diameter AB is produced to P, such that PC is a tangent to the semi-circle at C. Let Ĉ1 = x.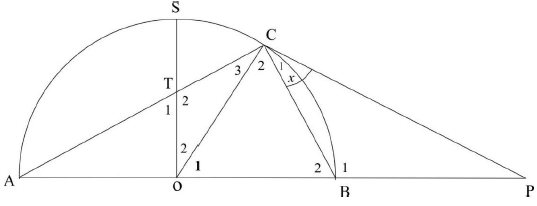
10.2.1 Write down, with reasons, 2 other angles equal to x. (3)
10.2.2 Prove that ∆TOC ⦀ ∆BPC (5)
10.2.3 Prove that TO.PC = OB.BP (2)
10.2.4 If BP = OB, show that 3OC2 = PC2(3) [19]
TOTAL: 150