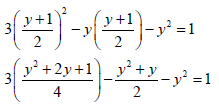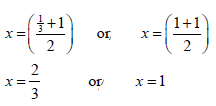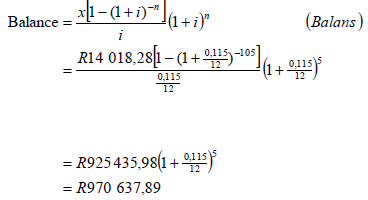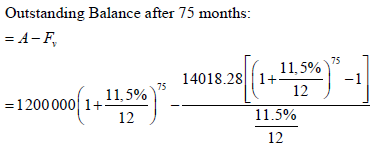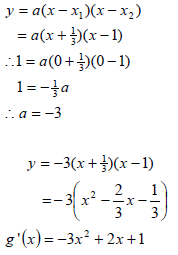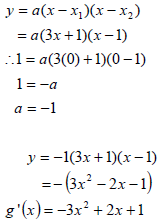Mathematics P1 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupNOTE:
- If a candidate answers a question TWICE, mark the FIRST attempt ONLY.
- Consistent accuracy applies in ALL aspects of the marking guideline.
- If a candidate crossed out an attempt of a question and did not redo the question, mark the crossed-out attempt.
- The mark for substitution is awarded for substitution into the correct formula.
MARKING SCHEMES
| QUESTION 1 | ||
| 1.1.1 | x2 - 3x - 4 = 0 (x + 1)(x - 4) = 0 x = -1 or 4 Answerd only: (2/3) OR can use quadratic formula 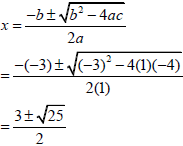 ∴ x = 4 or x = -1 | √ Factors √ x = -1 √ x = 4 √ correct substitution √ √ answers (3) |
| 11.2.2 | 2x2 - x - 7 = 0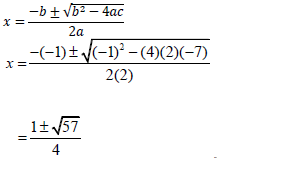 penalise 1 mark for incorrect rounding off x = 2,14 or -1,64 | √ substitution √ x = 2,14 √ x = -1,64 |
| 1.1.3 | 5x+1 - 5x = 2500 5x.51 - 5x = 2500 5x(5 - 1) = 2500 5x.4 = 2500 5x = 625 5x = 54 ∴ x = 4 | √ factorisation √ 5x = 625 √ x =4 |
| 1.1.4 | (x - 3)(x + 1) < 12 x2 - 2x - 3 - 12 < 0 x2 - 2x - 15 < 0 (x - 5)(x + 3) < 0 OR 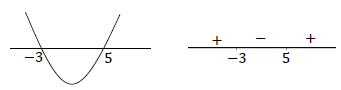 -3 < x < 5 OR x∈(-3;5) | √ standard form √ factorisation √√ -3 < x < 5 (accuracy) |
| 1.2 | y = 2x - 1 .......... (1) OR x = y + 1 .......(1) | √ y = 2x - 1
OR
√ x = y + 1 |
| 1.3 | f(x) = x2 - 2px + 8 + 2p OR b2 - 4ac = 0 | √ b2 - 4ac = 0
√ p values
√ b2 - 4ac = 0 |
| 2.1.1 | 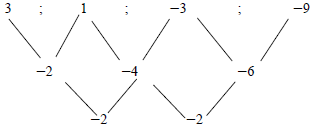 -17;-2 | √ both terms |
| 2.1.2 | 2a = -2 3a + b = -2 a + b + c = 3 ∴ a = -1 3(-1) + b = -2 -1 + 1 + c = 3 ∴ b = 1 ∴ c = 3 Tn = -n2 + n + 3 | √ a = -1 √ b = 1 √ c = 3 √ Tn = -n2 + n + 3 |
| 2.1.3 | -n2 + n + 3 = -809 n2 - n - 812 = 0 (n - 29)(n + 28) = 0 ∴ n = 29 | √ equating Tn to -809 √ factors √ choosing n = 29 |
| 2.2.1 | Tn = 2n - 3 T53 = 2(53) - 3 = 103 OR T53 = a + 52d = -1 + 52(2) = 103 | √ substitution into T53 √ answer √ substitution into T53 √ 103 |
| 2.2.2 | 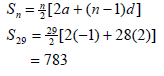 | √ substitution into correct formula √ 783 |
| 2.2.3 | √ √ 2n - 3 | |
| 2.3 | T4 = a + 3d and T10 = a + 9d ∴ T10 - T4 = 6d 6d = (8x - 2y) - (2x + y) = 6x - 3y ∴ d = x - ½y T4 = a + 3d 2x + y = a + 3(x - ½y) 2x + y = a + 3x - 3/2y ∴ a = 5/2y - x | √ T10 - T4 = 6d √ 6d = (8x - 2y) - (2x + y) √ d = x - ½y √ substitution √ value of a |
| QUESTION 3 | ||
| 3.1 | T1 = (x - 1) | √ -1 < r < 1 √ answer |
| 3.2 | When: 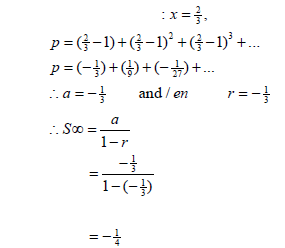 | √ substituting for x √ values for a and r √ substituting into S∞ formula √ answer |
| QUESTION 4 | ||
| 4.1 | x = -3 y = 1 | √ x = -3 √ y = 1 |
| 4.2 | 1 + 2 = 0 x + 3 2 = -1 x + 3 2 = -x - 3 x = -5 y = 1 + 2 0 + 3 = 5/3 | √ substitution √ x -intercept √ y-intercept |
| 4.3 | 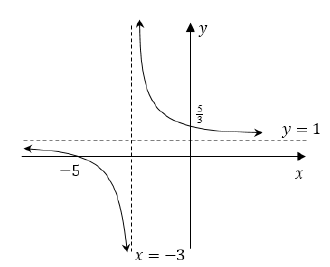 | √ asymptotes |
| 4.4 | h(x) = -2 - 1 OR h(x) = -2 - 1 | √ h(x) = -2 - 1
√ h(x) = -2 - 1 |
| QUESTION 5 | ||
| 5.1 | (0;-8) | √ answer |
| 5.2 | y = mx + c OR mTQ = 10 - (-8) | √ c = -8 √ substituting T(9;10) into equation of line √ equation |
| 5.3 | y = x2 - 7x - 8 = x2 - 7x + (-7/2)2 - 8 - (-7/2)2 = (x - 7/2)2 - 81/4 | √ completing the square √ equation |
| 5.4 | (7/2 ; -81/4) | √ x-coordinate √ y-coordinate |
| 5.5 | Ave gradient OR f'(x) = 2x - 7 | √ method
√ x2 - 7x - 8 - (10) = 1
√ equating to 1
|
| 5.6 | x2 - 7x - 8 = 0 ∴ x < -1 or 4 < x < 8 | √ x intercepts of f √ x intercept of g √ x < -1 accuracy √ 4 < x < 8 accuracy |
| QUESTION 6 | ||
| 6.1 | f(x) = logmx 3 = logm64 m3 = 64 m3 = 43 ∴ m = 4 | √ substitution √ answer |
| 6.2 | f(x) = log4x ∴ f-1 : x = log4x y = 4x | √ interchanging x and y √ answer |
| 6.3 | 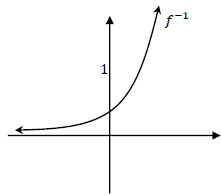 | √ y-intercept √ shape and asymptote |
| 6.4 | y > -2 OR y∈ (-2; ∞) | √ answer OR √ answer |
| QUESTION 7 | ||
| 7.1 | 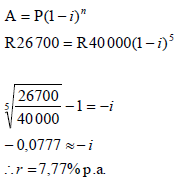 | √ substitution into correct formula √ simplification √ value for r |
| 7.2.1 | 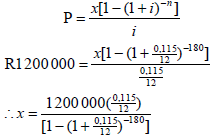 = R14 018,28 | √ i = 0.115/12 and n =180 √ substituting into correct formula √ answer |
| 7.2.2 (a) |
OR
= 2 453 828, 34 - 1528 392,76 Outstanding balance after 80 months; = 925 435,58 [1 + 11,5%]5 | √ ? = 105 for P and √ ? = 75 for both formulae
√ P(1 + 0,115)5 |
| 7.2.2 (b) | 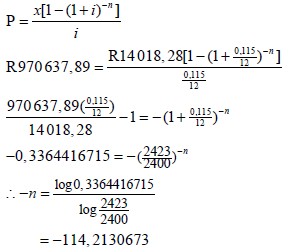 ∴ n = 115 months | √ P = R970 637,89 √ substituting into correct formula √ correct use of logs √ final answer |
| QUESTION 8 | ||
| 8.1 | 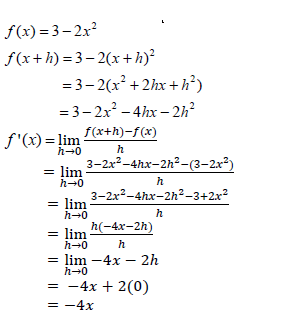 | √ 3 - 2x2 - 4hx - 2h2 √ substitution √ simplification √ factorisation √ answer |
| 8.2.1 | 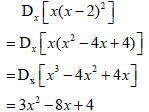 | √ x3 - 4x2 + 4x √ 3x2 √ - 8x √ +4 |
| 8.2.2 | 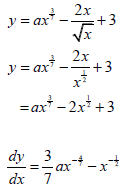 | √ -2x½ √ 3/7ax4/7 √ -x-½ (derivative of constant must be zero to get 3rd mark) |
| QUESTION 9 | ||
| 9.1 | x = -1/3 and x = 1 | √ x = -1/3 √ x = 1 |
| 9.2 | x = (1 + (-1/3)) ÷ 2 = 1/3 | √√ answer |
| 9.3 | g(x) is increasing when g'(x) > 0 -1/3 < x <1 OR x∈ (-1/3 ;1) | √√ answer |
| 9.4 |
OR
| √ substituting all intercepts
√ substituting all intercepts |
| 9.5 | g(x) = ax3 + bx2 + cx + d g'(x) = 3ax2 + 2bx + c = -3x2 + 2x + 1 ∴ 3a = -3 2b = 2 c = 1 ∴ a = -1 b = 1 ∴ y = -x3 + x2 + x + d + 1 0 = -03 + 02 + 0 + d + 1 ∴ d = -1 | √ g'(x) = 3ax2 + 2bx + c √ 3a = -3 √ 2b = 2 √ a = -1; b = 1; c = 1 √ substitute (0;0) into g(x) + 1 |
| QUESTION 10 | ||
| 10.1 | Let the two numbers be x and y : or y = 18 - 6 = 12 | √ x + y =18
|
| QUESTION 11 | ||
| 11.1.1 | a = 111 b = 106 | √ answer √ answer |
| 11.1.2 (a) | P(a boy who plays crickcet) = 108 or 54 530 265 | √ numerator √ denominator |
| 11.1.2 (b) | P(A or B) = P(A) + P(B) - P(A and B) OR P(girl or not tennis) | √ formula
√ method |
| 11.2.1 | 99 or 387 420 489 | √ 99 (1) |
| 11.2.2 | If vowels are together: 6! × 4! ∴ if vowels are not together: 9! - (6! × 4!) = 345 600 | √ 6! × 4! √ subtracting from 9! √ answer (3) |
| 11.2.3 | Vowels in odd spaces: = 4 × 5 × 3 × 4 × 2 × 3 × 1 × 2 = (4 × 3 × 2 × 1) × (5 × 4 × 3 × 2) = 4! × 120 = 2880 ∴ probability = 2880 (9 × 8 × 7 × 6 × 5 × 4 × 3 × 2) = 2880 362880 = 1 126 | √ 4! × 120 √ vowels in odd spaces (9 × 8 × 7 × 6 × 5 × 4 × 3 × 2) √ answer (4) [15] |
TOTAL: 150