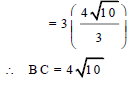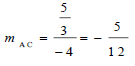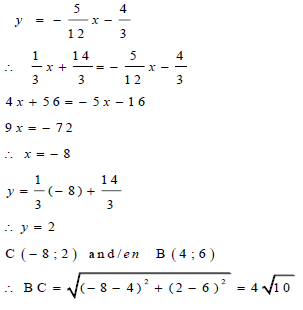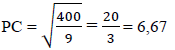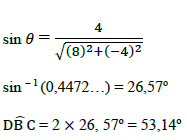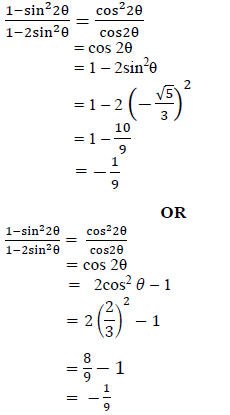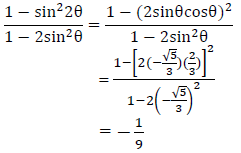Mathematics P2 Grade 12 Memorandum - NSC Exams Past Papers and Memos September 2019 Preparatory Examinations
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMARKING SCHEME
| QUESTION 1 | |||
| 1.1 | x = 420,8 80 = 5,26 | √ 420,8 80 √ answer | (2) |
| 1.2 | total of heights = 4,86 × 7 = 34,02 error = 4,98 - 4,89 = 0,09 new total heights = 33,93 new mean = 33,93 = 4,85m 7 | √ error = 0,09 √ new total √ answer | (3) |
| 1.3 | Standard deviation of individual heights of the 80 giraffes would be bigger than that of 7 males. There is a bigger spread of heights among population of juveniles and adults and babies. | √ bigger/larger standard deviation √ bigger spread of heights | (2) |
| [7] | |||
| QUESTION 2 | |||
| 2.1 | 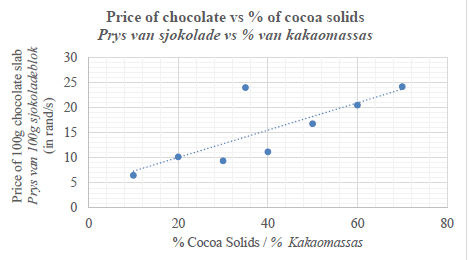 | √√ all points plotted correctly | (2) |
| 2.2 | y = a + bx a = 4,64 b = 0,27 y = 4,64 + 0,27x | √ value of a √ value of b √ equation | (3) |
| 2.3 | see line in 2.1 | √ correct gradient √ correct line | (2) |
| 2.4 | r = 0,78 | √ r = 0,78 | |
| 2.5 | fairly strong positive correlation in the % of cocoa and the price | √ correct description of r | (1) |
| 2.6.1 | Brand D OR (35;24) | √ answer | |
| 2.6.2 | y = 4,64 + 0,27(35) =R14,09 Overpriced by .R24,00 - R14,09 = R9,91 | √ substitution √ R14,09 √ R9,91 | (3) |
| [13] | |||
| QUESTION 3 | |||
| 3.1 | D(4;0) | √ answer | (1) |
| 3.2 | 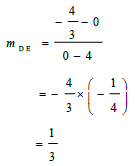 | √ substitution √ answer | (2) |
| 3.3 | Angle of inclination of DE = tan -11/3 = 18,43º ODE = 18,43º (vert.opp. ∠ s) OED = 71,57º (complementary ∠ s) ∴ PRB = 71,57º (corr. ∠ e: DE II BC) | √ tan -11/3 √ 18,43º √ answer √ reason | (4) |
| 3.4 | 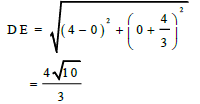 | √ substitution √ answer | (2) |
| 3.5 | AD = 3 = 1 AB 9 3 | √ ratios √ simplified answer | (2) |
| 3.6 | ΔABC III ΔADE OR equation of BC equation of AC | √ ratio of corresponding sides
OR √ equation of BC √ equation of AC | (3) |
| 3.7.1 | midpoint of DE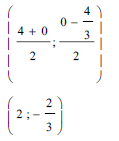 | √√ coordinates | (2) |
| 3.7.2 | mbisector = -3 Equation of bisector 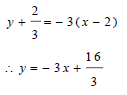 | √ gradient of bisector √ substitution √ equation | (3) |
| 3.8 | LHS = -3 RHS = -3(4) + 16/3 = - 20/3 = -62/3 ≈ -6,66 LHS # RHS No, bisector does not pass through A | √ substitution √ conclusion | (2) |
| [21] | |||
| QUESTION 4 | |||
| 4.1 | x2 - 6x + y2 = 16 (x - 3)2 + (y - 0)2 = 16 + 9 (x - 3)2 + (y - 0)2 = 25 Hence centre (3;0) Radius = √25 = 5 | √ completing the square √ final form √ taking square root | (3) |
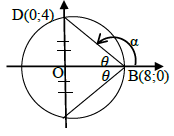
| 4.2.1 | y = 0 : hence (x - 3)2 = 25 x - 3 = ± 5 x = 3 ± 5 B (8 ; 0) OR 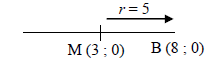 | √ equating = 0 OR √√√ use of horizontal distance | (3) |
| 4.2.2 | x = 0 : then (-3)2 + y2 = 25 OR using pythagoras : | √ equating x to 0 √ coordinates of C OR √ use of pythagoras √ coordinates of C | (2) |
| 4.3 | MCP = 90º OR POC = 90º | √ radius ⊥ tangent
| (3) |
| 4.4 |
OR
OR tan DBO = 4 = 1 | √ gradient of BD √ calculation of α √ angle θ √ doubling the angle OR √ sin definition √ use of arcsin √ angle θ √ doubling the angle OR √ tan ratio √ use of arctan to find angle √ angle √ doubling the angle | (4) |
| 4.5 | New circle centre OR Gradient of MC = 4/3 | √ coordinates of M and C OR √ gradient of MC | (4) |
| [19] | |||
| QUESTION 5 | |||
| 5.1.1 | 1 | √ answer | (1) |
| 5.1.2 | cos 2A | √ answer | (1) |
| 5.2.1 | 32 = 22 + k2 k = -√5 | √ distance formula pythagoras Thm √ answer with correct sign | (2) |
| 5.2.2 (a) | tan (θ -180º) tan θ = -√5 2 | √ reduction √ answer | (2) |
| 5.2.2 (b) |
OR
| √ 1 – sin22θ = cos2 2θ √ sin22θ = (2sinθcosθ)2 √ substitution for sin θ √ substitution for cos θ √ answer | (4) |
| 5.3 | sin (−200º).cos 310º + tan (−135º).cos 380º .sin 230º = sin (20º)(cos 50º) + (tan45º)(cos 20º)(−sin50º) = sin 20º cos 50º – (1)cos 20º sin 50º = sin (20º – 50º) = sin ( − 30º) = − ½ | √√√√ reductions to acute angles √ sin expansion √ answer | (6) |
| 5.4 | LHS= sin 2? + cos (2? – 90o) = sin 2? + sin 2? = 2 sin 2? = 2(2sin ? cos ?) = 4 sin ? cos ? = RHS/RK | √ cos (2θ – 90º) = sin 2θ √ simplification √ expansion | (3) |
| 5.5 | 10sin? + 10sin?.101=110 10sin?(1+10)=110 10sin?=101 ∴ sin x = 1 ∴ x = − 270º or/of x = 90º | √ split into product of 2 bases √simplification / factorisation √division by 11 √ equating the exponents √ both solutions | (5) |
| [24] | |||
| QUESTION 6 | |||
| 6.1 | 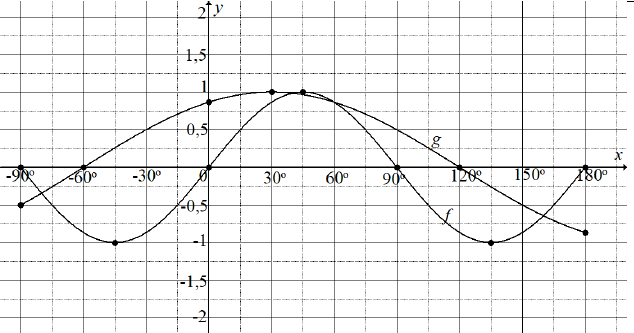 | √ completing f(x) = sin 2x graph | (1) |
| 6.2 | See graph in 6.1 | g(x) = cos (x – 30º) √ y intercept √ end points √ turning point √x intercepts | (4) |
| 6.3 | sin 2 x = sin (90º – ( ? – 30º)) sin 2 ? = sin (120º – ?) 2 ? = 120º − ? + k.360º or/of 2 ? = 180º – (120º − ?) + k. 360º 3 ? = 120º + k. 360º or/of ? = 60º + k. 360º ∴ ? = 40º + k. 120º or/of ? = 60º + k. 360º ; k ? Z k = 0 : ? = 40º ; 60º k = − 1 : ? = – 80º | √ co-ratio on RHS √ simplification √√ = 40º + k. 120º √ x = 60º + k. 360º √√ solutions | (6) |
| [11] | |||
| QUESTION 7 | |||
| 7.1 | tan y = PB | √ use of tan ratio √ PB = k.tan y √ BC = PB tan x | (3) |
| 7.2 | (AC)2 = (4,73)2 + (3)2 – 2(4,73)(3)( cos 100º) AC = 6,03 m | √ use of cosine rule √correct substitution in cosine rule √ answer | (3) |
| [6] | |||
| QUESTION 8 | |||
| 8.1.1 | BÂE = 90º ( ∠ in a semi-circle ) | √ statement / S √ reason / R | (2) |
| 8.1.2 | Ê1 = 40º ( sum of ∠ s of Δ ) | √ statement / S √ reason / R | (2) |
| 8.1.3 | C1 = 40º (∠s subtended by AB OR ∠s in the same segment) | √ statement / S √ reason / R | (2) |
| 8.1.4 | Ĉ2 = 62º (ext. ∠ of cyclic quad.) | √ statement / S √ reason / R | (2) |
| 8.1.5 | AB̂D = 62º (∠s subtended by AD OR ∠s in the same segment OR ext. ∠ of cyclic quad.) | √ statement / S √ reason / R | (2) |
| 8.2 | equal to the angle in the alternate segment/ | √ answer | (1) |
| 8.3 | R.T.P / Te Bewys: STUR cyclic OR R̂2 = 180º – (x + y) (3 ∠ s Δ) | √ statement / S √ reason / R √ S & R √ S & R √ opp. ∠ s of quad, supplementary | (5) |
| 8.4 | PN = NQ = 8 units (line from the centre ⊥ chord) M P2 = 62 + 82 (Pyth. Theorem) ∴ MP = 10 units MP = RM = MT = 10 (radii) ∴ RT = 20 units | √ S & R √ S & R √ S & R √ answer | (4) |
| [20] | |||
| QUESTION 9 | |||
| 9.1.1 | AD = AC n (prop theorem; DC II EF) DE CF 12 = AC 3 5 20 = AC | √ S & R √ Substitution √ answer | (3) |
| 9.1.2 | AO = 10 (diagonals of a parallelogram bisect) | √ answer | (1) |
| 9.1.3 | 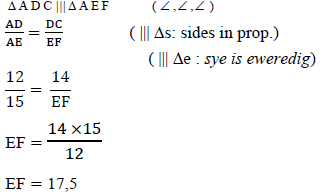 | √ S & R √ statement / S √ answer | (3) |
| 9.2 |  | (Area => Oppervlakte) OR √use of area rule | (3) |
| [10] | |||
| QUESTION 10 | |||
| 10.1 | 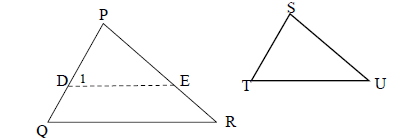 | (6) | |
| Construction: Mark D on PQ and E on PR such that PD = ST and PE = SU. Join DE. Proof: In ΔPDE and ΔSTU P ̂= Ŝ (given) PD = ST (construction) PE = SU (construction) ΔPDE ≡ ΔSTU (SAS) ∴ D̂1 = T ( ≡ Δ′?) But: Q̂ = T (given) ∴ D̂1 = Q̂ ∴ DE || QR (corr. ∠ s =) ∴ PD = PE (prop. theorem; DE || QR) PQ PR ∴ ST = SU PQ PR | √construction √ S & R √ D̂1 = T̂ √ D̂1 = Q̂ √ reason for lines∥ √ prop. theorem;DE || QR ;DE||QR | ||
| 10.2.1 | Â = x (tan chord thm) Ĉ3 = x (angles opp. = sides) | √ statement(S) √ reason(R) √ S & R | (3) |
| 10.2.2 | R.T.Ps: ΔTOC ⦀ Δ BPC ACB = 90º ( ∠ in the semi-circle) Proof : Ĉ3= Ĉ1 = ? (proved) T̂2 = 90º + ? (ext. ∠ of Δ) B̂1 = 90º + ? (ext. ∠ of Δ) ∴ T̂2 = B̂1 ∴ Ô2 = P̂ (sum of ∠ s in Δ) ∴ ΔTOC ⦀ Δ BPC (∠ , ∠ ,∠ ) OR ACB = 90º ( ∠ in the semi-circle) B2 = 90° − ? (sum of ∠s in Δ) ∴ P = 90° − 2? (ext. ∠of Δ) O1 = 2? (∠ at centre = 2 × ∠ at circum.) ∴ O2 = 90° − 2? (SO ⊥ AB) ∴ O2 = P ?3 = ?1 = ? (proved above) ∴ ΔTOC|||ΔBPC(∠, ∠, ∠) | √ S & R OR √ S & R | (5) |
| 10.2.3 | R.T.P : TO.PO = OB.BP Proof : TO = OC BP PC But OC = OB (radii) ∴ TO = OB BP PC ∴ TO.PC = OB.BP | √sides in prop. √ S | (2) |
| 10.2.4 | in ΔOPC: OP2 = OC2 + PC2 (pyth.theorem) But : OB = OC = BP (radii) ∴ (20C)2 = OC2 + PC2 4OC2 = OC2 + PC2 ∴ PC2 = 3OC2 | √ S & R √ OB = OC = BP √(2OC)2 = OC2 + PC2 | (3) |
| [19] | |||
| TOTAL: | 150 | ||