PHYSICAL SCIENCES PAPER 1 GRADE 12 QUESTIONS - NSC EXAMS PAST PAPERS AND MEMOS MAY/JUNE 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupPHYSICAL SCIENCES PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE EXAMINATIONS
MAY/JUNE 2021
INSTRUCTIONS AND INFORMATION
- Write your centre number and examination number in the appropriate spaces on the ANSWER BOOK.
- This question paper consists of TEN questions. Answer ALL the questions in the ANSWER BOOK.
- Start EACH question on a NEW page in the ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Leave ONE line between two subquestions, e.g. between QUESTION 2.1 and QUESTION 2.2.
- You may use a non-programmable calculator.
- You may use appropriate mathematical instruments.
- Show ALL formulae and substitutions in ALL calculations.
- Round off your FINAL numerical answers to a minimum of TWO decimal places.
- Give brief motivations, discussions, etc. where required.
- You are advised to use the attached DATA SHEETS.
- Write neatly and legibly.
QUESTION 1: MULTIPLE-CHOICE QUESTIONS
Various options are provided as possible answers to the following questions. Choose
the answer and write only the letter (A–D) next to the question numbers (1.1 to 1.10) in
the ANSWER BOOK, e.g. 1.11 E.
1.1 A constant net force acts on an object moving in a straight line. Which ONE of the following quantities associated with the object will remain constant during the motion?
- Velocity
- Momentum
- Acceleration
- Kinetic energy (2)
1.2 The weight of an object on the surface of the Earth is w. What will be the weight of the object on the surface of another planet of the SAME mass as that of the Earth, but TWICE the radius of the Earth?
- ¼w
- ½w
- 2 w
- 4 w (2)
1.3 The diagram below shows a cricket player moving his hands downwards from position 1 to 2 to 3 while catching a ball.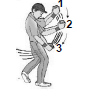
Which ONE of the following statements CORRECTLY explains why the cricket player moves his hands downwards?
- The impulse on the ball is decreased.
- The change in momentum of the ball is increased.
- The change in momentum of the ball is decreased.
- The time it takes to change the momentum of the ball is increased. (2)
1.4 Consider the motion of a small stone thrown vertically upwards until it reaches its maximum height.
Ignore the effects of friction.
Which ONE of the following combinations of graphs CORRECTLY shows how the momentum p and the gravitational potential energy U of the stone change with time?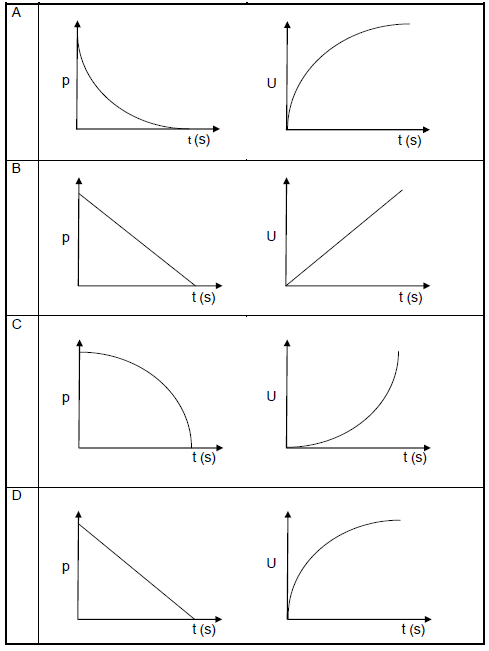
1.5 A boy and a girl, having DIFFERENT masses, are initially at rest at point P. They slide down different paths of a water slide, as shown in the diagram below.
Ignore the effects of friction.
Consider the statements below regarding the boy and the girl:
- Only conservative forces act on both the boy and the girl while they are sliding downwards.
- The boy and the girl each have the same gravitational potential energy at point P.
- On reaching point Q, the speed of the girl is equal to that of the boy.
Which of the above statements is/are CORRECT?
- I only
- I and III only
- II and III only
- I, II and III (2)
1.6 An astronomer observes that the light spectrum of a star has been blue shifted.
How have the observed frequency of light from the star and the distance between the star and Earth changed?
| OBSERVED FREQUENCY OF LIGHT | DISTANCE BETWEEN THE STAR AND EARTH |
| A. Increased | Increased |
| B. Increased | Decreased |
| C. Decreased | Increased |
| D. Decreased | Decreased |
(2)
1.7 A small negative point charge (q) is situated halfway between two identical spheres, P and Q, carrying IDENTICAL charges, as shown below.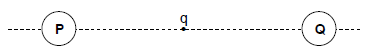
Sphere P exerts an electrostatic force of magnitude F on sphere Q. What is the magnitude of the net electrostatic force experienced by the point charge?
- Zero
- ½F
- F
- 2F
1.8 Consider the statements below regarding AC power and DC power:
- AC voltage can be changed during AC power transmission.
- DC power transmission requires transformers.
- AC power transmission is more energy efficient.
Which of the above statement(s) is/are CORRECT?
- I only
- II only
- I and III only
- II and III only (2)
1.9 In the circuit diagram below, all resistors are IDENTICAL. Ignore the internal resistance of the cell and the resistance of the connecting wires.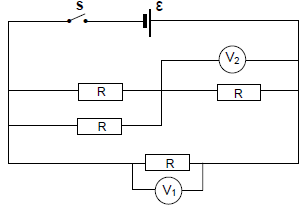
When switch S is CLOSED, the reading on voltmeter V1 is 3 V.
What will be the reading on voltmeter V2?
- 1 V
- 1,5 V
- 2 V
- 3 V (2)
1.10 Some of the energy levels of an atom are represented in the diagram below.
E0 represents the ground state energy.
Which ONE of the energy transitions below represents the absorption of light of the lowest frequency by the atom?
- E0 to E4
- E1 to E3
- E3 to E4
- E0 to E3 (2)
[20]
QUESTION 2 (Start on a new page.)
An 8-kg block, on a rough horizontal surface, is connected to a 2-kg block by a light inextensible string passing over a frictionless pulley, as shown below. The 8-kg block moves at a constant speed when pulled by a 29,6 N horizontal force to the right. The frictional force acting on the 8-kg block is 10 N.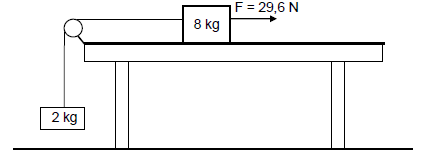
2.1 State Newton's Second Law of Motion in words. (2)
2.2 Draw a labelled free-body diagram for the 8-kg block. (5)
2.3 Calculate the tension in the string. (3)
The 29,6 N horizontal force is now increased to 50 N.
2.4 Apply Newton's Second Law to EACH block and calculate the:
2.4.1 Magnitude of the acceleration of the 8-kg block (5)
2.4.2 Tension in the string (2)
[17]
QUESTION 3 (Start on a new page.)
A ball, of mass 0,06 kg, is thrown vertically upwards from the balcony of a building, 3 m above the ground. The ball reaches a maximum height h above the ground, as shown in the diagram below.
Ignore the effects of air resistance.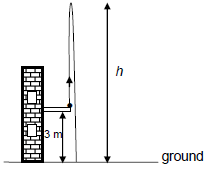
3.1 Name the force acting on the ball while it is in free fall. (1)
The velocity-time graph below represents the motion of the ball from the instant it is thrown upwards until it hits the ground.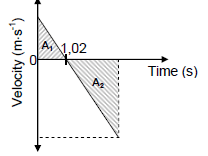
3.2 Write down the acceleration of the ball at time t = 1,02 s. (2)
3.3 Consider the areas A1 and A2 shown in the graph above. Write down the numerical value represented by the DIFFERENCE in areas A1 and A2. (1)
3.4 Calculate the:
3.4.1 Speed at which the ball is thrown upwards (3)
3.4.2 Height h (4)
After hitting the ground, the ball bounces vertically upwards and reaches a new maximum height in 1,1 s.
3.5 Calculate the work done by the ground on the ball while the ball is in contact with the ground. (6)
[17]
QUESTION 4 (Start on a new page.)
A simple rocket system consists of two parts, A of mass 3m, and B of mass 2m, as shown in the diagram below. B is stacked on top of A.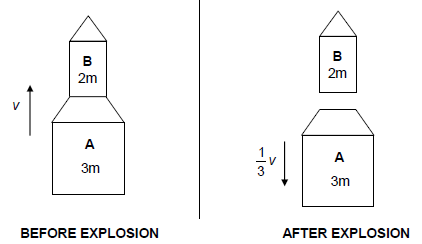
4.1 State the principle of conservation of momentum in words. (2)
The rocket is travelling vertically upwards at a constant speed v when an internal explosion causes A to move DOWNWARDS at a speed
Ignore ALL external forces on the rocket.
4.2 Calculate the velocity of B in terms of v immediately after the internal explosion. (5)
The graph below shows the average force exerted by A on B during the internal explosion as a function of time.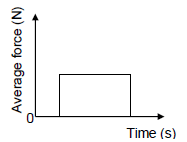
4.3 Name the physical quantity represented by the area under the graph. (1)
4.4 Redraw the graph in your ANSWER BOOK. On the same set of axes, sketch the graph of the average force that B exerts on A as a function of time. (2)
[10]
QUESTION 5 (Start on a new page.)
A demolition ball is used by a crane to break the wall of a building.
The demolition ball, of mass 1 250 kg, is lifted by the crane to a point R at a height of 5,8 m above its lowest position in 60 s.
Ignore air friction.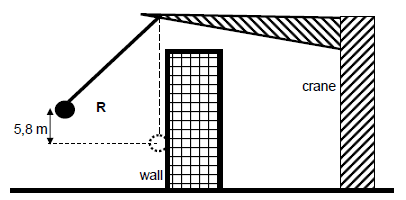
5.1 Define the term power in words. (2)
5.2 Calculate the average power dissipated by the crane in lifting the demolition ball to point R.(3)
The demolition ball is released from point R and strikes the wall at the lowest point of its swing. The ball then moves 0,25 m HORIZONTALLY into the wall before coming to rest.
5.3 Define the term conservative force. (2)
5.4 Is the force which the wall exerts on the ball a CONSERVATIVE or a NON-CONSERVATIVE force? (1)
5.5 State the energy conversion that takes place during the downward swing of the demolition ball. (1)
5.6 Using energy principles, calculate the magnitude of the average force exerted on the ball while it moves into the wall. (5)
[14]
QUESTION 6 (Start on a new page.)
A learner in a car, moving at a constant speed of 10 m·s-1 along a straight horizontal road, records the frequency of sound emitted by a distant stationary source.
The learner then repeats the recording of the frequency of the sound when the car travels at a new constant speed of 20 m·s-1.
The graph below, not drawn to scale, is obtained from the results.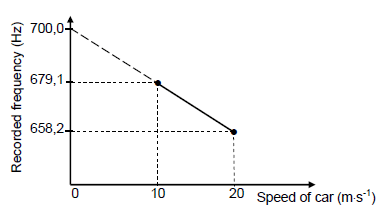
6.1 State the Doppler effect. (2)
6.2 Use the graph to answer the following questions.
6.2.1 Write down the frequency of the sound emitted by the stationary source.
Give a reason for the answer. (2)
6.2.2 In which direction is the car moving relative to the source?
Choose from TOWARDS or AWAY.
Give a reason for the answer. (2)
6.2.3 Calculate the speed of sound in air.(5)
[11]
QUESTION 7 (Start on a new page.)
Two charged spheres, R and S, are both stationary on a smooth, insulated surface inclined at an angle of 25° to the horizontal. Sphere S, of mass 0,01 kg and carrying a charge of –6 x 10-9 C, is connected to a 0,03 m long, light inextensible string attached to point P at the top of the incline.
Sphere R, carrying a charge of +5 x 10-9 C, is held such that the distance between the centres of the spheres is r, as shown in the diagram below.
Ignore the effects of friction.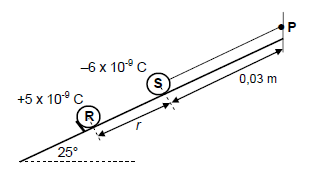
Sphere R exerts an electrostatic force of magnitude 1,2 x 10-3 N on sphere S.
7.1 State Coulomb's law in words. (2)
7.2 Calculate the distance r between the spheres. (3)
7.3 Draw a labelled free-body diagram for sphere S. (4)
7.4 Calculate the:
7.4.1 Tension in the string (4)
7.4.2 Net electric field at point P (5)
[18]
QUESTION 8 (Start on a new page.)
Three resistors are connected to a battery with an unknown emf and unknown internal resistance r, as shown below.
Ignore the resistance of the connecting wires.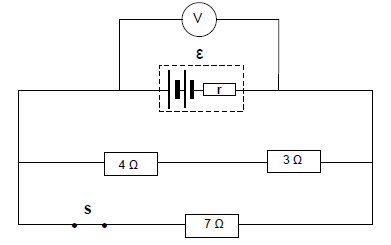
8.1 In the definition of the emf of a battery given below, (a) and (b) represent missing words or phrases.
The emf of the battery is the maximum (a) … supplied by a battery per (b) …. passing through it.
Write down (a) and (b) in your ANSWER BOOK and next to each the missing word or phrase. (2)
With switch S CLOSED, the voltmeter reads 2,63 V.
8.2 Calculate the equivalent external resistance of the circuit. (4)
Switch S is now OPENED and the voltmeter reads 2,8 V.
8.3 Calculate:
8.3.1 The internal resistance of the battery (8)
8.3.2 The emf of the battery (2)
[16]
QUESTION 9 (Start on a new page.)
The diagram below is a simplified representation of an AC generator. The coil is rotated in a clockwise direction in the magnetic field.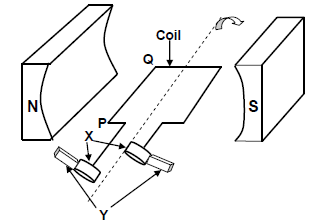
9.1 Write down the name of component X. (1)
9.2 Write down the function of component Y. (1)
9.3 Use the relevant principle to explain why an emf is induced in the coil when the coil is rotated in the magnetic field. (2)
9.4 The coil rotates CLOCKWISE from the position shown in the diagram. In which direction will current be induced in segment PQ of the coil?
Choose from 'P to Q' or 'Q to P'.(2)
The output voltage versus time graph below was obtained for the above generator.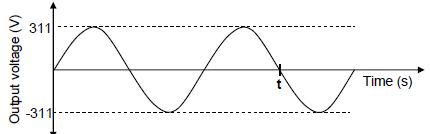
The output voltage is generated at a frequency of 50 Hz.
9.5 Calculate the time t indicated in the above graph. (3)
9.6 The generator is now connected to an appliance with a resistance of 100 Ω. Calculate the energy dissipated when the appliance is in operation for ONE minute.(5)
[14]
QUESTION 10 (Start on a new page.)
When light of various frequencies is incident on the metal cathode of a photocell, photoelectrons are emitted from the surface of the cathode.
The graph below shows the relationship between the maximum kinetic energy (Ek(max)) of an emitted photoelectron and the wavelength of the incident light.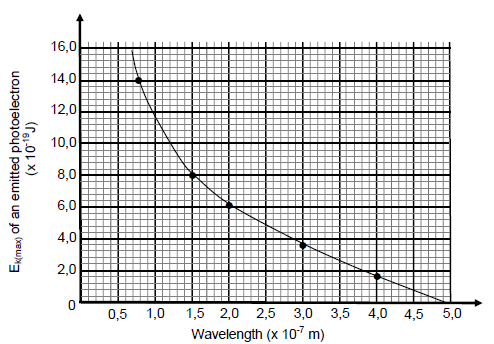
10.1 Use the graph to determine the maximum kinetic energy of the emitted photoelectron when the wavelength of the incident light is 1,0 x 10-7 m. (1)
10.2 What relationship between the maximum kinetic energy of the emitted photoelectron and the wavelength of the incident light can be deduced from the graph? (2)
10.3 Define the term work function in words. (2)
10.4 Use the graph to calculate the work function of the metal used as cathode of this photocell. (4)
10.5 Calculate the maximum kinetic energy of the emitted photoelectron when the wavelength of the incident light is 0,5 x 10-7 m. (4)
[13]
TOTAL: 150
DATA FOR PHYSICAL SCIENCES GRADE 12
TABLE 1: PHYSICAL CONSTANTS
NAME | SYMBOL | VALUE |
Acceleration due to gravity | g | 9,8 m•s-2 |
Universal gravitational constant | G | 6,67 × 10-11 N•m2•kg-2 |
Speed of light in a vacuum | c | 3,0 × 108 m•s-1 |
Planck's constant | h | 6,63 × 10-34 J•s |
Coulomb's constant | k | 9,0 × 109 N•m2•C-2 |
Charge on electron | e | -1,6 × 10-19 C |
Electron mass | me | 9,11 × 10-31 kg |
Mass of earth | M | 5,98 × 1024 kg |
Radius of earth | RE | 6,38 × 103 km |
TABLE 2: FORMULAE
MOTION
| vf = vi + aΔt | Δx = ViΔt + ½aΔt2 or Δy = ViΔt2 + ½aΔt2 |
Vf2 = Vi2 + 2aΔx or Vf2 = vi2 + 2aΔy | Δx = [Vi + Vf]Δt or Δy = [Vi + Vf]Δt |
FORCE
Fnet = ma | p= mv |
fsmax = µsN | fk = µkN |
FnetΔt = Δp | w =mg |
F = Gm1m2 | g = G M |
WORK, ENERGY AND POWER
W =FΔxcosθ | U= mgh or EP = mgh |
K = ½mv2 or Ek = ½mv2 | Wnet = ΔK or Wnet = ΔEk ΔK = Kf −Ki or ΔEk =Ekf − Eki |
Wnc= ΔK + ΔU or Wnc= ΔEk + ΔEp | P = W Δt |
Pav = Fv |
WAVES, SOUND AND LIGHT
v = f λ | T =1/f |
fl = v ± vl fs fl = v ± vl fb | E = hf or E = h c |
E = W0 + Ek where | |
ELECTROSTATICS
| F = kQ1Q2 r2 | E = KQ |
E = V | E = F |
V = W | n = Q |
ELECTRIC CIRCUITS
R = V | emf (ε) = I(R + r) |
RS = R1 + R2 + ....... | q = I Δt |
W = Vq | P= W |
ALTERNATING CURRENT
I rms = Imax | Paverage = VrmsIrms |