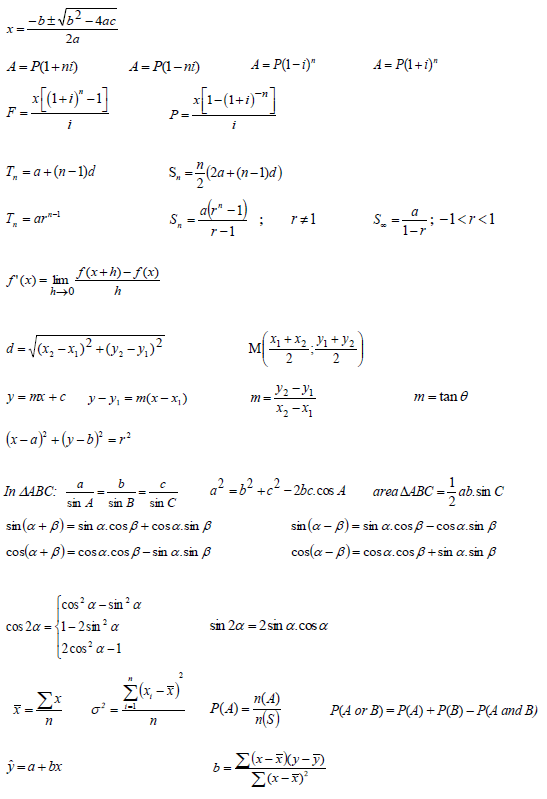INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of ELEVEN questions. Answer ALL the questions.
2. Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answer.
3. You may use an approved scientific calculator (non-programmable and non- graphical), unless stated otherwise.
4. Answers only will not necessarily be awarded full marks.
5. If necessary, round off answers to TWO decimal places, unless stated otherwise.
6. Diagrams are NOT necessarily drawn to scale.
7. Number the answers correctly according to the numbering system used in this question paper.
8. An information sheet with formulae is included at the end of the question paper.
9. Write neatly and legibly.

QUESTIONS

QUESTION 1
1.1 Solve for x:
1.1.1 x² + 2x -15 = 0 (3)
1.1.2 3x² + x -1 = 0 (correct to TWO decimal places) (3)
1.1.3 x(x - 3) ≥ -2 (4)
1.1.4 √43 - x - x +1 = 0 (5)
1.2 Solve simultaneously for x and y:                2 y - x = 3 and  y² + 3x = 2xy         (5)

1.3 The roots of a quadratic equation are given as follows: 

Determine the value(s) of p for which the equation will have non-real roots. (4)
[24]

QUESTION 2
2.1 Given the quadratic number pattern: -16 ; -16 ; -12 ; -4 ; ...
2.1.1 Write down the next term of the pattern. (1)
2.1.2 Determine the general term of the pattern in the form T_n = an² + bn + c     (4)
2.1.3 Calculate the value of the 38th term of the pattern. (2)
2.1.4 Determine which two consecutive terms of the pattern will have a difference of 400. (3)
2.2 Given the arithmetic series: 2 + 5 + 8 + . . . +89 = k , calculate:
2.2.1 the number of terms in the series. (2)
2.2.2 the value of k . (3)
[15]

QUESTION 3
3.1 Given that in a geometric sequence T₉ = 768 and T₁₃ = 12288 . Determine the value(s) of the common ratio and the first term of the sequence. (3)
3.2 The sum to infinity of a convergent geometric series is ⁵⁴/₁₉ . The sum to infinity of the same series calculated from the 3rd term is ²⁴/₁₉ .
3.2.1 Calculate the sum of the first two terms of the series. (1)
3.2.2 Show that: (1)
3.2.3 Determine the value of r, if r > 0  (4)
[9]

QUESTION 4
The diagram below shows the graphs of and g(x) = b^x , where b > 0. A and C are x and y-intercepts of f respectively, while D is the y-intercept of g. is a point that lies on g.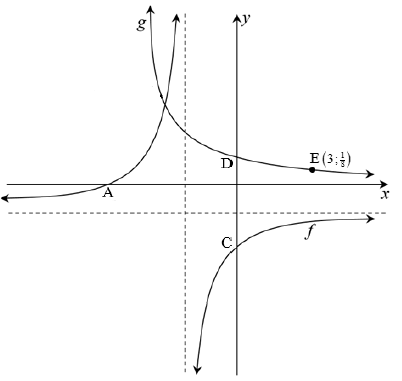

4.1 Write down the coordinates of D. (1)
4.2 Write down the equations of asymptotes of f. (2)
4.3 Write down the domain of f. (2)
4.4 Determine the value of b. (2)
4.5 Determine the coordinates of A and C. (3)
4.6 Write down the equation of g ^-1, in the form y = ... (2)
4.7 Determine the values of x for which:
4.7.1 f (x).g(x) > 0 (2)
4.7.2 g ^-1(x) ≥ 3 (2)
[16]

QUESTION 5
The diagram below shows the graph of f (x) = -x² - 2x + 8 . R and S are x-intercepts and V the y-intercept of f . T is the turning point of f.

5.1 Determine the length of RS. (4)
5.2 Determine the coordinates of T. (3)
5.3 The gradient of the tangent to the graph f at a point W is equal to 2.
5.3.1 Determine the coordinates of W. (4)
5.3.2 Determine the equation of a straight line, g , which is perpendicular to the tangent and passing through V. (2)
5.4 The graph of f is shifted one unit to the right and then reflected in the x-axis to produce a new function h. Determine the equation of h in the form:
h(x) = ax² + bx + c.   (4)
[17]

QUESTION 6
6.1 Eli bought a laptop 4 years ago. The value of the laptop depreciates from R9 670,00 on a reducing-balance method to its current value of R5 509,70. Calculate the annual rate of depreciation of the laptop. (3)
6.2 Mr Duda decided to save money towards his son’s tertiary education as follows:

• He paid R600 per month into an account that paid 8,7% interest p.a. compounded monthly.
• His first payment was at the end of January in which his son started Grade 1 and the last payment at the end of December when his son completed his Grade 12. His son did not repeat any grade.
• He withdrew all his savings one month after his last payment.

Calculate the amount that was in his account by the time Mr Duda withdrew all the savings.  (4)
6.3 Pilisa takes out a loan to buy a car that costs R350 000. The bank offers her an interest rate of 9,3% p.a. compounded monthly and a payment period of 6 years. Her first instalment is due at the end of the first month after taking the loan.
6.3.1 Calculate Pilisa’s monthly instalment. (3)
6.3.2 Calculate the balance of her loan after the 40th payment was made. (3)
6.3.3 Pilisa decides to increase her monthly instalment to R7 000 per month after her 40th payment. How long, after the 40th payment, will it take her to pay up the loan? (4)
[17]

QUESTION 7
7.1 Determine f '(x) from first principles if f (x) = 5 - 2x² . (5)
7.2 Determine:
7.2.1  (3)

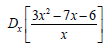7.2.2 (4)
[12]

QUESTION 8
8.1 The diagram below shows the graph of f (x) = 2x³ + bx² + cx + d. Points J(–1 ; 0), K( ½ ; 0) and L(3 ; 0) are the x-intercepts and G the y-intercept of f. M and N are the turning points and H the point of inflection of f.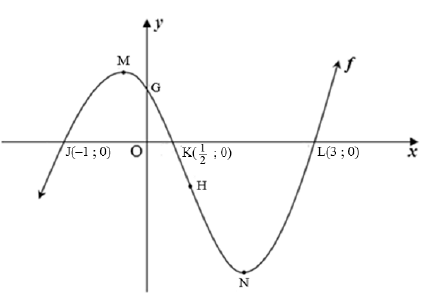

8.1.1 Determine the values of b, c and d in the equation of f. (4)
8.1.2 If it is given that f (x) = 2x³ - 5x² - 4x + 3 , determine the coordinates of N, the minimum turning point of f. (4)
8.1.3 For which values of x , is:

1. f' (x) < 0? (2)
2. f concave down ? (3)

8.2 If g(x) = px³ + qx² + rx is a cubic function that further satisfies the following conditions:

• p < 0
• g '(m) = g(m) = 0, where m > 0

Draw a sketch graph of g clearly indicating one of the turning points of g in terms of m and all intercepts.  (3)
[16]

QUESTION 9
The diagram below shows a solid triangular prism. The triangle is right-angled with a height of 8x metres, a base of 15x metres, and a hypotenuse of 17x metres as indicated on the diagram. The length of the prism is y metres and the total surface area of the prism is 5 760 m².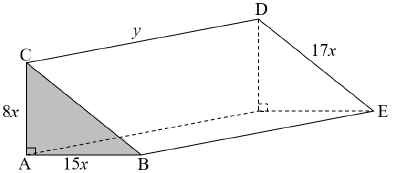

9.1 Show that    (2)
9.2 Hence, show that the volume of the prism can be expressed as:  V(x) = 8640x -180x³.  (2)
9.3 Determine the value of x for which the volume of the prism will be a maximum. (4)
[8]

QUESTION 10
10.1 A and B are two independent events such that P(A) = 0,2 and P(not B) = 0,45. Determine:
10.1.1 P(B) (1)
10.1.2 P(A or B) (3)
10.2 Asanda travels to school on her bike or by taxi. The probability that she travels by taxi is x. If she uses her bike, the probability that she will be late for school is ²/₅ and if she travels by taxi, the probability that she will be late is ¹/₂. Determine the value of x if the probability that Asanda is not late for school is ⁸/₁₅ . (4)
[8]

QUESTION 11
In a certain province vehicle number plate codes have the following format:
@ @ @ # # # (three letters followed by 3 digits) where @ represents a letter of the alphabet and # a digit from 0 to 9. For each number plate code that is assigned to a vehicle, the following conditions must be met:

• All letters except E, G and O can be used and no letter can be repeated.
• No number plate code can start with a vowel.
• All digits can be used, and each digit can be repeated.

11.1 How many vehicles can be assigned a number plate code according to this system? (3)
11.2 Calculate the probability that a number plate code chosen from the number plates in QUESTION 11.1 at random contains only one vowel and ends with
an even digit. (5)
[8]

TOTAL: 150

INFORMATION SHEET: MATHEMATICS