Mathematical Literacy Paper 2 Questions - Grade 12 September 2021 Preparatory Exams
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupINSTRUCTIONS AND INFORMATION
- This question paper consists of FIVE questions.
- Use the ANNEXURE in the ADDENDUM to answer the following questions:
- ANNEXURE A for QUESTION 2.1
- ANNEXURE B for QUESTION 4.1
- Answer ALL the questions.
- Number the questions correctly according to the numbering system used in this question paper.
- Maps and diagrams are NOT necessarily drawn to scale, unless stated otherwise.
- Round off ALL the final answers appropriately according to the context used, unless stated otherwise.
- Indicate units of measurement, where applicable.
- Start EACH question on a NEW page.
- Show ALL calculations clearly.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1
South Africans require the following tablets to boost their immune systems during winter. The pictures below show two types of prescriptions to use namely vitamin C and Zinc capsules:
The table below shows the types of essential vitamins adults consume daily to keep their immune system strong.
NOTE: Adults use 2 capsules daily per prescription. |
Study the table above and answer the questions that follow.
1.1.1 Write as a ratio in simplified form the Zinc mg per tablet to Vitamin C mg per tablet. (2)
1.1.2 Calculate how many milligrams of Zinc an adult takes per week. (3)
1.1.3 Mr Smith purchased the Vitamin C tablets on the 28th February 2021. He decided to use the medicine as prescribed daily from the next day. Determine by which date he will need a refill of Vitamin C tablets. (3)
1.1.4 Determine the total number grams of Zinc contained by an entire bottle of Zinc. (3)
1.2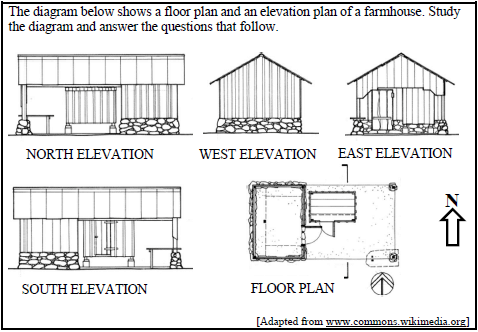
1.2.1 Explain the meaning of ‘North Elevation’ on the diagram. (2)
1.2.2 Refer to the diagram above. Define the following terms respectively:
- A floor plan (2)
- An elevation plan (2)
1.2.3 Use the scale of 1 : 100 to determine the actual length in centimetres on the plan if the measured length is 5 cm. (2)
1.3
Mr Dudley, a farmer, travels from his farm to the city once a week. The distance from the city to his farm is 90 km. He plans to buy 4 boxes of tiles to replace some broken tiles in his kitchen. |
1.3.1 Convert 90 km to mm. (2)
1.3.2 Calculate the number of tiles packed in ONE box, if the area of 1 tile is 0,36 m2 and the tiles are sold at 1,44 m2 per box. (2)
1.3.3 Mr Dudley takes 1,125 hours to travel to town. Convert this time to hours, minutes, and seconds. (3)
[26]
QUESTION 2
2.1
The Fisher family, consisting of the wife, husband and son, plans to spend the festive season with friends in Gqeberha (Port Elizabeth) and then proceed to Johannesburg.
A map of South Africa and all the national routes are shown on ANNEXURE A. |
Study the map on ANNEXURE A to answer the questions that follow.
2.1.1 Write down the names of TWO towns they will be passing through on their trip to Port Elizabeth. (2)
2.1.2 Give TWO general directions used when travelling from Cape Town to Johannesburg via Port Elizabeth. (4)
2.1.3 State TWO advantages of using national roads. (4)
2.1.4 Use the bar scale on ANNEXURE A to calculate the actual distance between Cape Town and Port Elizabeth. Show ALL calculations. Give your answer to the nearest km. (4)
2.1.5 The Fisher family is travelling at an average speed of 100 km/h. Prove by means of calculations whether they will be able to reach Port Elizabeth at the planned time.
The following formula may be used: Distance = Average Speed x Time (7)
2.2
The price of petrol is 1 642 cents per litre. Mr Fisher drives a Jeep Wrangler with a fuel capacity of 75 litres. The Jeep has a fuel consumption of 7,6 litres per 100 km. |
2.2.1 Calculate the amount of petrol that will be used for a return trip to Port Elizabeth. (4)
2.2.2 Determine the petrol cost for the return trip in rands (R) from Cape Town to Port Elizabeth. (3)
[28]
QUESTION 3
3.1
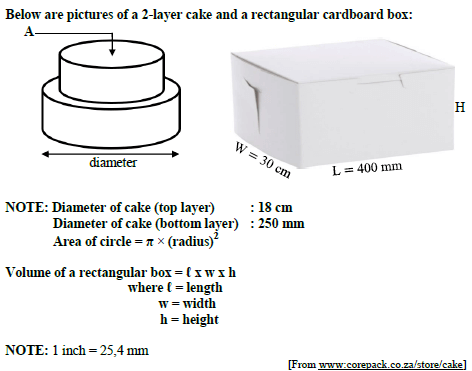
Mr Johnathan and his wife decided to arrange a birthday party for their only daughter. They purchased a two layered round chocolate cake at a bakery. The diameter of the bottom layer is 250 mm and the diameter of the top layer is 18 cm.
|
Refer to the diagram above and answer the questions that follow.
3.1.1 Determine A, the area indicated on the top layer of the chocolate cake in square millimetres (mm2). Give your answer to the nearest whole millimetres. (5)
3.1.2 A ribbon will be wrapped around the circumference of the bottom layer cake and must overlap by 50 mm. Calculate the length of the ribbon in mm.
You may use the formula:
Circumference = 2 × π × radius where π = 3,142 (4)
3.1.3 The volume of the rectangular cardboard box is 42 000 cm3. Determine the height of the box in cm. (4)
3.1.4 Mr Johnathan’s cousin in England claims that the diameter of the bottom layer cake is more than 10 inches. Verify with the necessary calculation if his claim is valid or not. (3)
3.1.5 According to the baker at the bakery, the height of the bottom layer of the cake is 64% of the radius. Calculate the height of the bottom layer in mm. (3)
3.1.6 The recipe for the chocolate cake needs flour to sugar in a ratio of 7 : 3. Determine the number of cups of flour needed if 6 cups of sugar are used. (3)
3.1.7 Mr Johnathan’s wife plans to bake a similar one-layer chocolate cake for a tea party. She received the recipe from a friend in the United Kingdom. According to the recipe, the baking temperature should be at 365 °F (Fahrenheit). Determine the temperature in degrees Celsius. Give your answer to the nearest 10 degrees Celsius.
You may use the following formula: °C = (°F – 32°) ÷ 1,8 (3)
3.2
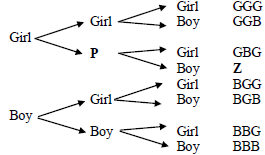
Mr Johnathan and his wife plan to have two more children. Study the diagram below:
|
3.2.1 Identify the type of diagram shown above. (2)
3.2.2 Write down the appropriate items for P and Z. (2)
3.2.3 Determine the probability for Mr Johnathan and his wife of:
- Getting at least two girls (as a fraction in simplified form) (3)
- Getting a boy, then a girl, then a boy (as a percentage) (2)
[34]
QUESTION 4
4.1
ANNEXURE B shows the drawing of the floor plan of a low-cost house. Study the floor plan and answer the questions that follow. |
4.1.1 Identify the feature you will find upon entering the bathroom. (2)
4.1.2 Write down the number of windows facing southwards. (2)
4.1.3 Determine the length of the interior bathroom wall (excluding the door) that is not given, if the door takes up a space of 860 mm. (6)
4.2
The kitchen and bathroom should be tiled. The floor tile dimension is 500 mm x 500 mm. When buying tiles, you need to buy 5% more to cater for breakages. A tiling company charges R8 186,09 for labour and can get the tiles at R249,90 per box.
|
Refer to the information above to answer the questions that follow.
4.2.1 Calculate the total area that must be tiled in m2. (9)
4.2.2 The building manager made the statement that 150 tiles are needed to complete tiling for the kitchen and bathroom. Verify with a calculation whether his statement is valid or not. (7)
4.2.3 The tiling company charged R24 795,00 for the cost of tiles and labour. The manager of the low-cost housing claims that the tiling company's quotation is exceptionally high. Verify, with the necessary calculations, whether the manager's claim is valid or not.
NOTE: Each box has 4 tiles. (6)
[32]
QUESTION 5
5.1
A young rugby player is concerned about his weight. He weighs himself before joining a gymnasium and calculates that his BMI (Body Mass Index) is 25,1 kg/m2. He has a height of 175 cm. The table below shows the weight status versus the BMI ranges. TABLE 2: WEIGHT STATUS ACCORDING TO BMI
|
Refer to the table provided above and answer the questions that follow.
5.1.1 Use the information above to calculate his current weight (mass). You may use the formula below:
BMI = Mass in kg (4)
(Height × Height) in metres
5.1.2 Write down the young player’s current weight status. (2)
5.1.3 Provide advice to him on how to improve his BMI status. (2)
5.2
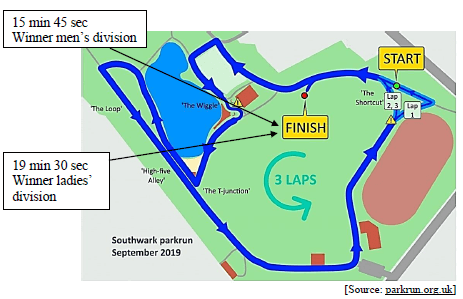
The map of Southwark Park Run course is shown below. Runners are required to complete 3 laps to finish the race. A parkrun is a 5 000 m distance run. On a certain Saturday, Douglas Cameron was the winner of the men's division with a time of 15 min 45 seconds. Sarah Caroll, a fellow park run tourist at Southwark Park was the winner of the lady’s division with a time of 19 min 30 seconds.
|
Study the information and map above and answer the questions that follow.
5.2.1 If the total distance is 5 000 m, determine the length of 1 lap in kilometres. (3)
5.2.2 Douglas Cameron was very unfit when he started off participating in park runs and did not complete all his laps initially. He claims that he completed a total distance of 23,33 km for his first 5 park runs. Prove by calculation whether his statement is valid. Refer to the table below.
TABLE 3: SUMMARY OF DOUGLAS CAMERON’S PARK RUN RACES (5)
Date of park run | Distance in metres | Number of laps completed |
07/09/2019 | … | 2 |
14/09/2019 | … | 2 |
21/09/2019 | 5 000 | 3 |
28/09/2019 | 5 000 | 3 |
05/10/2019 | 5 000 | 3 |
5.2.3 Sarah Caroll made the statement that the difference in minutes between her average time per lap of 6,5 minutes (6 min 30 sec) and Douglas’ average time per lap is less than 2 minutes. Verify with the necessary calculations whether her statement is valid. (5)
5.3
James decided to distribute candles to local churches. He would like to pack cylindrical candles into a rectangular container for distribution. Each candle is 11 cm high and measures 8 cm in diameter.
|
Study the picture and diagram above and answer the questions that follow.
5.3.1 James realises that he can pack the candles on top of each other if he places a support that is 10 mm thick, between the layers. The container that he uses is 24 cm high, 16 cm wide and 24 cm long. Calculate how many candles he can pack into this container. (5)
5.3.2 James prints a label that covers the sides of the container. Calculate the area of the label in m2. You may use the following formula:
Area of all sides = 2 (length × height) + 2 (width × height) (4)
[30]
TOTAL: 150