Technical Mathematics Paper 1 Questions - Grade 12 September 2021 Preparatory Exams
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupINSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of NINE questions.
- Answer ALL the questions.
- Answer QUESTION 4.1.5 and QUESTION 7.4 on the ANSWER SHEETS provided. Write your name and school name in the spaces provided on the ANSWER SHEETS and hand in the ANSWER SHEETS with your ANSWER BOOK.
- Number the answers correctly according to the numbering system used in this question paper.
- Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise. If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is attached at the back of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
1.1 Solve for x:
1.1.1 21x2 +13x = 0 (2)
1.1.2 x + 5 = 7 (correct to TWO decimal places) (4)
x
1.1.3 –5x2 – 4x + 1 ≥ 0 (3)
1.2 Solve the following systems of equations simultaneously: 2x+ y = 1 and x2 + y2 + 2x - 6y = 9 (7)
1.3 The speedometer below shows the speed of a car travelling at 110 km/h.
1.3.1 Express 110 km/h in m/s, if 1m = 1 000 km. (1)
1.3.2 Write the solution in QUESTION 1.3.1 above, in Scientific Notation. (1)
1.4 Convert 315 to binary notation, WITHOUT using a calculator. (2)
[20]
QUESTION 2
2.1 Given: (x - √23)(x - √23) = 0
2.1.1 Write down the number of root(s) the above equation has. (1)
2.1.2 Hence, or otherwise, describe the nature of the root(s). (3)
2.2 The sketch below represents the graph of a function f defined by f (x) = ax2 + bx+3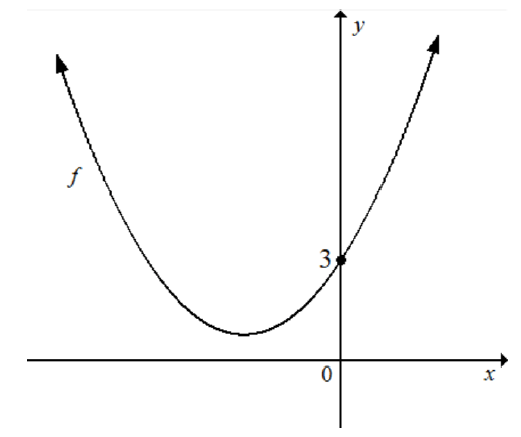
Use the graph above to answer the following questions.
Given:
| OPTION | Value of a | Value of b |
| P | 1 | 3 |
| Q | ½ | 3 |
| R | -1 | 3 |
| S | 1 | -3 |
Using the information given in the table above, choose any option(s) that will satisfy the condition that the roots of f are imaginary. (2)
[6]
QUESTION 3
3.1 Simplify without using a calculator.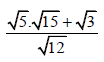 (4)
(4)
3.2 Show (without using a calculator) that: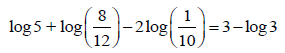 (5)
(5)
3.3 Solve for n:
3.22n +1 – 8n – 1 = 4n (4)
3.4 The accompanying graph shows an Argand diagram of a complex number, z, with point P (5 ; – 3):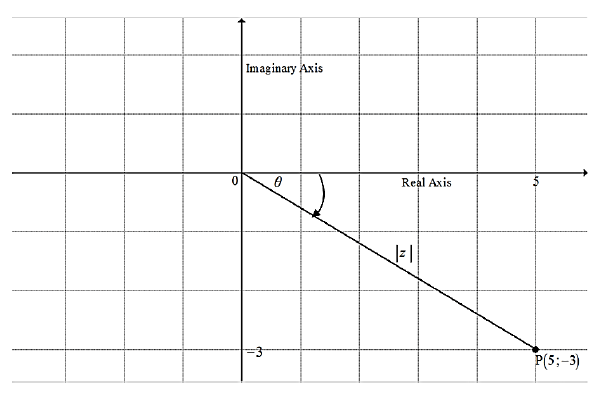
3.4.1 Write down the complex number in rectangular form, z = a + bi (1)
3.4.2 Calculate the modulus of z. (2)
3.4.3 Express the complex number as z = r cisθ (4)
3.5 Solve for x and y if: (2 - 3i)i + 7y + 9 =11 + 13ix (5)
[25]
QUESTION 4
4.1 Given the functions f (x) = 2x -1 and k (x) = 1 - 1
x
4.1.1 Determine the coordinates of the x-intercept of f . (3)
4.1.2 Write down the equation of an asymptote of f. (1)
4.1.3 Write down the equations of asymptotes of k. (2)
4.1.4 Determine the x-intercept of k. (2)
4.1.5 Sketch the graphs of f and k on the ANSWER SHEET provided, indicating the asymptote(s) and intercept(s) of the graphs. (5)
4.1.6 Write down the domain of k. (1)
4.1.7 Write down the range of f. (2)
4.2 Sketched below are the graphs of g (x) = a( x - p)2 + q and h( x) = √9 - x2 .
- Points A, B and C are the intercepts of h.
- x = – 1 and point C are the x-intercepts of the graph of g.
- Point D is the y-intercept of g.
- E(p ; – 4) is the turning point of g.
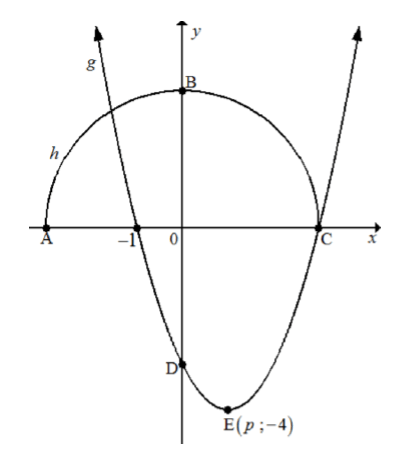
4.2.1 Write down the numerical value of q. (1)
4.2.2 Determine the coordinates of C. (2)
4.2.3 Calculate the numerical value of p, the x-coordinate of point E. (2)
4.2.4 Determine the numerical value of a. (3)
4.2.5 Hence, or otherwise, determine the coordinates of D. (1)
4.2.6 Determine the values of x ≥ 0 for which h (x) > g (x). (2)
[27]
QUESTION 5
5.1 Determine the effective interest rate of 4,5% nominal interest rate per annum, compounded monthly. (3)
5.2 The table below shows pressure readings over time taken on a car tyre using a pressure gauge, as shown in FIGURE 1. The pressure readings are taken over a period of 5 minutes. Pressure is measured in kilo Pascals (kPa).
The graph, with A as the y-intercept, alongside in FIGURE 2, represents the points recorded in the table below.
TIME (Minutes) | PRESSURE (kPa) |
0 | 350 |
1 | 210 |
2 | 126 |
3 | 75,6 |
4 | 45,36 |
5 | 27,216 |
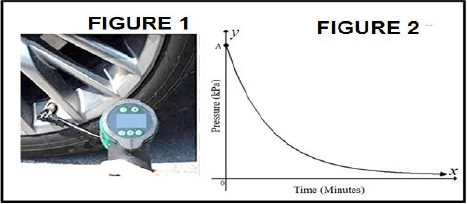
5.2.1 Write down the y-coordinate of point A as shown in the graph. (1)
5.2.2 Which rate best describes the change in pressure over 5 minutes?
Hint: Refer to the table or FIGURE 2. (1)
- Compound increase
- Simple interest
- Compound depreciation
- Straight Line Depreciation
5.2.3 Hence, or otherwise, determine the rate at which the tyre pressure changes over 5 minutes. (4)
5.3 An amount of R50 000 is invested at an interest rate of 6,5% per annum, compounded quarterly for the first 5 years of the investment. The interest rate then changes to 5% per annum, compounded monthly for the remaining 3 years of the investment. Determine the amount of money accumulated by the investment at the end of the 8-year investment period. (5)
[14]
QUESTION 6
6.1 Determine the derivative of f (x) = 13ax - 2b by using FIRST PRINCIPLES. (5)
6.2 Determine:
6.2.1 dy if x(-6x + y) = x3 (4)
dx
6.2.2 ![]() (4)
(4)
6.3 Determine the average gradient of g (x) = x2 + 3x – 4 between x = – 2 and x = 1. (3)
[16]
QUESTION 7
Given: f (x) = – x3 + 6x2 – 11x + 6
7.1 Write down the y-intercept of f. (1)
7.2 Determine the x-intercepts of f. (4)
7.3 Determine the coordinates of the turning points of f. (5)
7.4 Sketch the graph of f on the ANSWER SHEET provided, showing all the intercepts and the turning points of f. (5)
7.5 Determine the possible value(s) of x for which h(x) = –11x + q is a tangent to f . (4)
[19]
QUESTION 8
The diagram below shows, a quick industrial reaction between hydrogen gas and nitrogen gas, in the presence of a catalyst, to produce liquid ammonia known as the Haber process. The amount of ammonia produced is proportional to the temperature at that particular time. The heat of reaction is a function of time, ?(?) = −2?2 + 20? + 400; ? ≥ 0 measured in ºC and time (t) in seconds.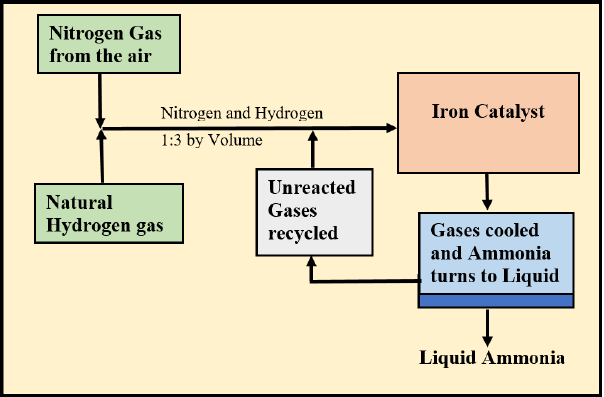
Determine:
8.1 The heat at the start of the reaction (1)
8.2 The heat (H) after 3 seconds (2)
8.3 The time taken to change from freezing temperature to maximum temperature (8)
[11]
QUESTION 9
9.1 Determine the following integrals:
9.1.1 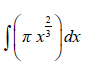 (2)
(2)
9.1.2 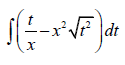 (3)
(3)
9.2 The sketch below shows the shaded area bounded by the curve of the function defined by f (x) = x3 – x and the x-axis between points x = – 1 and x = 1.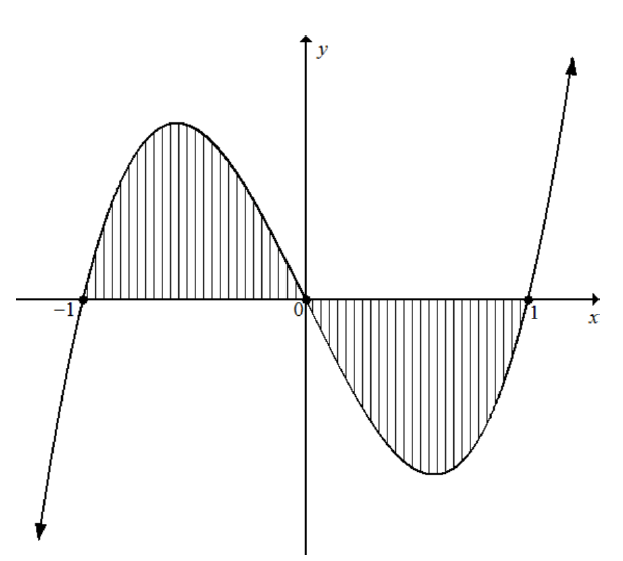
Determine (showing ALL calculations) the shaded area bounded by the curve f and the x-axis between the points where x = − 1 and x = 1. (7)
[12]
TOTAL: 150
INFORMATION SHEET: TECHNICAL MATHEMATICS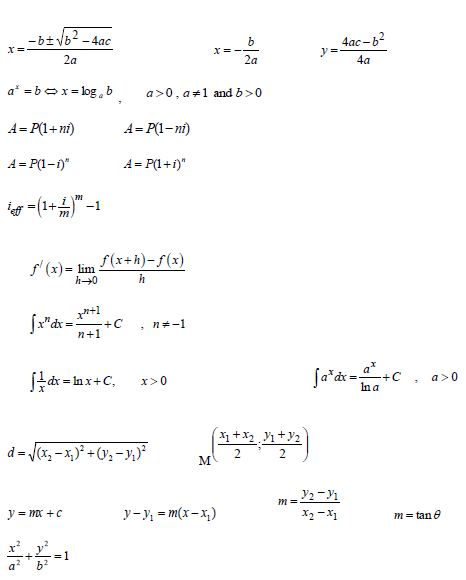

ANSWER SHEET
SURNAME: ………………………………….. NAME: ……………………………………….
SCHOOL: ………………………………………. CLASS: ………………………………………
QUESTION 4.1.5
ANSWER SHEET
SURNAME: …………………………………….. NAME: ……………………………………….
SCHOOL: ………………………………………. CLASS: ………………………………………
QUESTION 7.4