INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of ELEVEN questions.
2. Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
3. Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining the answers.
4. Answers only will NOT necessarily be awarded full marks.
5. You may use an approved scientific calculator (non-programmable and non- graphical) unless stated otherwise.
6. If necessary, round off your answers to TWO decimal places, unless stated otherwise.
7. Diagrams are NOT necessarily drawn to scale.
8. An information sheet with formulae is attached at the back of the question paper.
9. Write neatly and legibly.

QUESTIONS

QUESTION 1
In the diagram below, A(−5; 0), B(−2; ?), C(3; −4) and D are points on the Cartesian plane. AO ∥ BC and the inclination of DC is ?. BC cuts the ?-axis at E.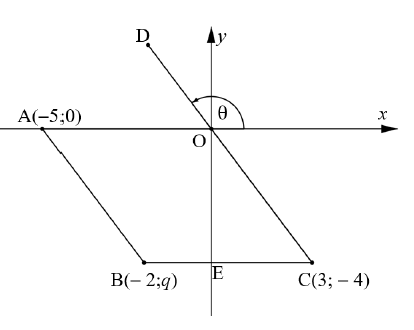

Determine:
1.1 The value of ? (1)
1.2 The length of AB (2)
1.3 The size of ? (3)
1.4 The type of quadrilateral represented by ABCO (4)
[10]

QUESTION 2
2.1 Consider the equations of the circle ?² + ?² = 25 and straight line ? − ? − 1 = 0
Determine:
2.1.1 The coordinates of the points of intersection of the line and the circle (7)
2.1.2 Whether the point (3; 2) lies inside, or outside, or on the circle (3)
2.1.3 The equation of the tangent to the circle at point (−4; 3) in the form ? = … (4)
2.2 Plot the graph of the ellipse 36?² + 49?² = 1 764 on the grid provided in the SPECIAL ANSWER BOOK. (4)
[18]

QUESTION 3
3.1 If  = 210,5° and B̂ = 122,3°, determine the values of the following correct to ONE decimal place:
3.1.1 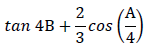 (2)
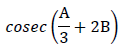3.1.2 (3)

3.2 Consider 12???A = 5 and 90° < Â < 360° . Determine the value of the following, without the use of a calculator:
3.2.1 ?????²A (5)
3.2.2 ???A − ?i?A (3)
3.2.3 Determine the size of  , with the use of a calculator. (3)
[16]

QUESTION 4
4.1 Simplify:            ?i?(? − ?). ?????(2? − ?). ???(? + ?)   (8)
                                          ???(2? − ?). ???(2? − ?) 
4.2 Prove the identity:
    ????     − ???? = ????  (5)
1 − ?i??
[13]

QUESTION 5
Given ƒ(?) = sin(? − 30°) and ?(?) = ???3? for ? ∈ [0°; 180°]
5.1 Use the set of axes provided in the SPECIAL ANSWER BOOK to draw sketch graphs of the curves of f and g for ? ∈ [0°; 180°]. Clearly show ALL intercepts with the axes, coordinates of all turning points and end points of both curves. (6)
5.2 Use the graphs drawn in QUESTION 5.1, or otherwise, to determine the following:
5.2.1 The period of g (1)
5.2.2 The value(s) of ? ∈ [0°; 180°] for which:

1. ƒ(?) = ?(?) (2)
2. ƒ(?). ?(?) ≥ 0 (2)

[11]

QUESTION 6
The diagram below shows a vertical rectangle, ABCD. B, E, F and C are on the same horizontal plane. AB ⊥ BE, DC ⊥ BF, BÊA = 60°, BĈE = 30°, DC = 8 cm and EC = 9 cm. EF = ? and CÊF = ?. B, C and F are collinear.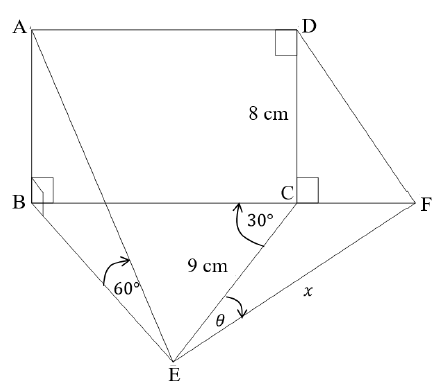

6.1 Write down the length of AB, stating a reason. (2)
6.2 Determine the length of BE, round off to the nearest integer. (2)
6.3 Determine the size of EB̂C, round off to the nearest degree. (3)
6.4 Determine the area of ∆BCE. (3)
6.5 Determine the length of CF, to the nearest integer, if ? = 25° and ? = 10 cm. (3)
[13]

QUESTION 7
7.1 Complete the following statement:  “The angle subtended by an arc at the centre of a circle is …”   (1)
7.2 The diagram below shows a circle with centre ?. ?, ? and ? are points on the circumference of the circle. OD = OE and BÔE = 48°. DE is a tangent at ?.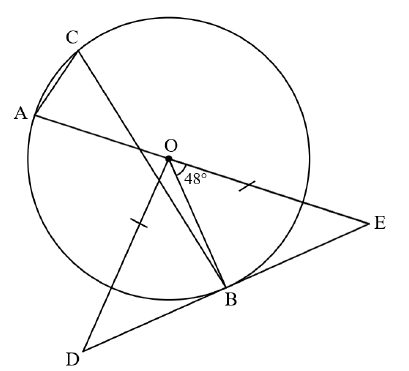

Determine, stating reasons, the size of the following angles:
7.2.1 AÔB (1)
7.2.2 Ĉ (2)
7.2.3 A?̂D (3)
7.2.4 AÔD (2)
7.2.5 If the diameter of the circle is 10 cm and OE = 7 cm, determine the length of BE. (3)
[12]

QUESTION 8
8.1 Complete the following statement:  “The opposite angles of a cyclic quadrilateral are …” (1)
8.2 Circle PQRST is drawn below. PŜQ = 58°, ̂P = 72°, Û = 22° and T̂ = ?.

8.2.1 Write down, stating reasons, the size of the following angles in terms of ?:

1. QŜR (2)
2. PQ̂R (3)

8.2.2 Determine the value of ?. (2)
[8]

QUESTION 9
9.1 Name TWO conditions for triangles to be similar. (2)
9.2 In the diagram below, C, E and D are points on the circumference of a circle. CF is a tangent to the circle at C. FĈD = 52°.

9.2.1 Prove that ∆CDF ∆ECF. (4)
9.2.2 Hence, show that CF2 = EF. FD. (2)
9.2.3 If EF = 15 cm and ED = 6 cm, determine the length of CF to the nearest integer. (4)
9.2.4 Determine CD : EC in simplified form. (2)
9.2.5 Further, if EĈD = 44°, explain whether CE is a diameter of the circle. (2)
[16]

QUESTION 10
10.1 In the diagram below EC and BG are the arc lengths of circle sectors with different radii, that both subtend an angle of 30°. The radii, AG, of the smaller sector is 4 cm and BE is 5 cm.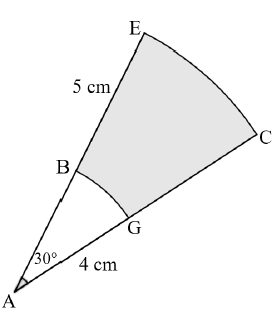

10.1.1 Convert  to radians. (2)
10.1.2 Determine the arc length of BG. (3)
10.1.3 Determine the area of sector AEC. (3)
10.1.4 Hence, determine the area of the shaded area BECG. (4)
10.2 Two pulleys are connected by a belt so that one pulley rotates. The linear speeds of the belt and both pulleys are the same. The radius of the smaller pulley is 3 cm, and the radius of the larger pulley is 15 cm. The smaller pulley is turning at 120 revolutions per minute.

10.2.1 Determine the angular velocity of the smaller pulley. (3)
10.2.2 Hence, determine the linear velocity of the smaller pulley. (3)
10.2.3 Hence, determine the angular velocity of the larger pulley. (3)
10.3 In the diagram below, FG is the diameter of the circle, with a length of 10 cm. CD is a chord of the circle with a length of 8 cm. CD divides the circle into two segments.

Determine the height of the smaller segment.  (5)
[26]

QUESTION 11
11.1 Consider the irregular figure below.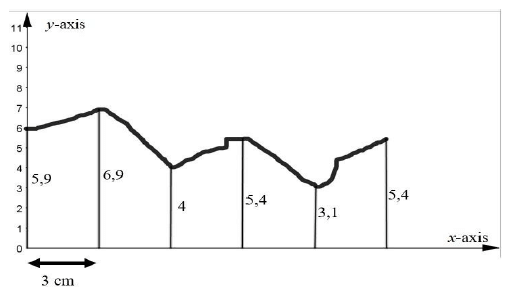

Determine the area of the figure by using the mid-ordinate rule. (4)
11.2 Mr Hlazo wants to collect rainwater from his roof, in a cylindrical tank, to irrigate his garden. The tank needs to be painted. The diameter of the tank is 1,85 ? and the outer height of the tank is 2,5 ?. The tank has an opening at the top with a diameter of 1 ?.

The following formulae may be used:

• Total surface area of a right cylinder = 2??² + 2??ℎ
• Volume of a right cylinder = (??²) × ℎ?i?ℎ?

Calculate the surface area of the cylindrical tank that will be painted. (3)
[7]
TOTAL: 150

INFORMATION SHEET