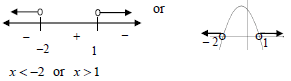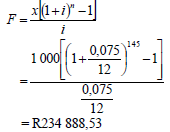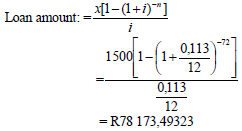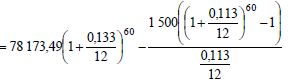MATHEMATICS PAPER 1 GRADE 12 MEMORANDUM - NSC EXAMS PAST PAPERS AND MEMOS NOVEMBER 2020
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE
MEMORANDUM
NOVEMBER 2020
NOTE:
- If a candidate answers a question TWICE, only mark the FIRST attempt.
- Consistent accuracy applies in all aspects of the marking memorandum.
REMEMBER: (A) next o the description of a tick implies accuracy mark
QUESTION 1
1.1.1 | x 2 - 6x = 0 | common factor |
1.1.2 | x2 + 10x + 8 = 0 | substitution into the correct formula |
1.1.3 | (1- x)(x + 2) < 0 | critical values |
1.1.4 | x +18 = x - 2 | squaring both sides (m) |
| 1.2 | x + y = 3 OR | y subject of the formula OR |
| 1.3 | n200 < 5300 OR OR OR | (n2)100 < (53 )100 n2 < 125 11 (3) OR OR OR |
QUESTION 2
2.1 | 7 ; x ; y ; –11 ; … OR OR | 7 + 3d = –11 OR OR |
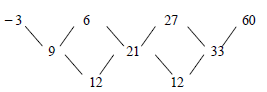
2.2.1 | -3 ; 6 ; 27 ; 60 ; … | second difference |
| 2.2.2 | T50 = 6(50)2 - 9(50) | substitute 50 |
| 2.2.3 | 9 ; 21 ; 33 ; … | a and d |
| 2.2.4 | - 3 + Sn = 21060 OR | - 3 + Sn = 21060 equation standard form answer (4) equation |
| [17] |
QUESTION 3
3.1 |
| 12 + 4 + 4/3 +... or 36(1/3) |
3.2 | a = 4.32- p | expression for a |
[8] |
QUESTION 4
| 4.1.1 | x = 1 y = 2 | x = 1 y = 2 (2) |
| 4.1.2 | y = mx + c or or = -(x -1) + 2 | substitution of m = –1 and (1 ; 2) answer(2) |
| 4.1.3 | 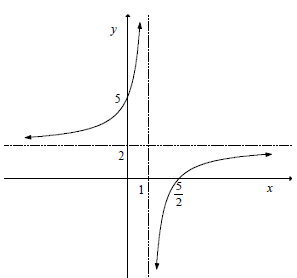 | vertical asymptote: x = 1 and horizontal asymptote: y = 2 x-intcept: 5/2 y-intercept: 5 shape (A) |
| 4.2.1 | (–5 ; –8) | x = - 5 y = - 8 (2) |
| 4.2.2 | y ≥ - 8 or [-8;∞] | answer |
| 4.2.3 | m = –5 n = g(–5) = ½(-5) + 9/2 = 2 | m = –5 substitution n = 2 |
| 4.2.4 | 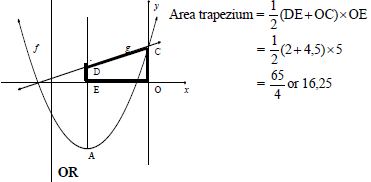 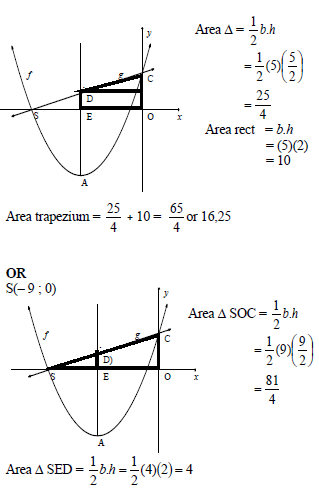 | method or or |
| 4.2.5 | g-1: x = ½y + 9/2 g-1: y = 2x - 9 | changing x and y answer |
| 4.2.6 | f (x) =½(x + 5)2 - 8 OR | f / (x) OR |
| [23] |
QUESTION 5
5.1 | A(0 ; 1) | answer (1) |
5.2 | 9 = 3-x | equating |
5.3 | x ∈(0;∞) or x > 0 | answer (2) |
5.4 | h(x) = 27.3 -x | h(x) = 3-(x-3) |
5.5 | 27 < 1 3-x+3 < 1 OR | 3x > 27 or 3-x+3 < 30 OR |
[12] |
QUESTION 6
6.1.1 |
| n = 145 |
6.1.2 | A = P(1+ i)n | substitution into the correct formula |
6.2 | A = P(1- i)n | substitution into the correct formula |
6.3.1 |
| 72 |
6.3.2 |
Amount paid: R1 500 x 60 = R90 000 OR | substitution (A) OR |
| [16] |
QUESTION 7
Penalty of – 1 for notation only in 7.1
7.1 | f (x) = 2x2 - 1 | 2x2 + 4xh + 2h2 -1 |
7.2.1 | d (5√x2 + x3) | x2/5 |
7.2.2 | f (x)= 4x2 - 9 f / (x) = 1 | (2x - 3)(2x + 3) |
[12] |
QUESTION 8
8.1 | -1 < x < 2 | answer (2) |
8.2 | x = -1 + 2 | method |
8.3 | From the graph x > ½ | answer |
8.4 | g (x) = ax3 + bx2 + cx | g / (x) = 3ax2 + 2bx + c |
8.5 | g /(½) = 6(½)2 + 6(½) + 12 | max gradient at x =½ |
[15] |
QUESTION 9
9.1 | Total surface area = 2?w + 2wh + 2?h | 2?w + 2wh + 2?h |
9.2 | 5 = 3w2h | h = 5 |
[10] |
QUESTION 10
10.1 | 1010 or 10 000 000 000 | answer (2) |
10.2.1 | 8 × 10 × 10 x 8 × 8 × 10 x 2 × 10 × 10 × 10 | 8 × 10 × 10 |
10.2.2 | Probability = 1,024 x 109 | 1,024 x 109 |
[7] |
QUESTION 11
| 11 | 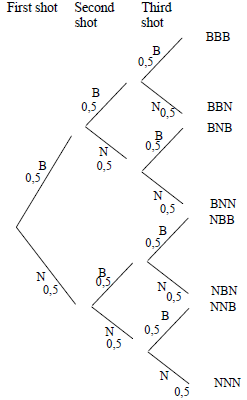 | |
| 11.1 | P (Bull’s eye first shot and second shot) | two 0,5’s |
11.2 | P (Bull’s eye at least twice in 3 shots) | 0,5 × 0,5× 0,5 |
11.3 | Person shoots first: | (0,5) + (0,5)3 |
[8] | ||
TOTAL: 150