MATHEMATICS PAPER 2 GRADE 12 QUESTIONS - NSC EXAMS PAST PAPERS AND MEMOS NOVEMBER 2020
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupMATHEMATICS PAPER 2
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2020
INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 10 questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers correct to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTION 1
A Mathematics teacher was curious to establish if her learners' Mathematics marks influenced their Physical Sciences marks. In the table below, the Mathematics and Physical Sciences marks of 15 learners in her class are given as percentages (%).
| MATHEMATICS (AS %) | 26 | 62 | 21 | 33 | 53 | 76 | 32 | 59 | 43 | 33 | 49 | 51 | 19 | 34 | 85 |
| PHYSICAL SCIENCES (AS %) | 34 | 67 | 28 | 46 | 65 | 76 | 26 | 73 | 50 | 39 | 57 | 51 | 24 | 41 | 80 |
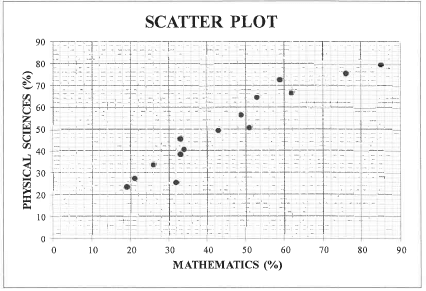
1.1 Determine the equation of the least squares regression line for the data.(3)
1.2 Draw the least squares regression line on the scatter plot provided in the ANSWER BOOK. (2)
1.3 Predict the Physical Sciences mark of a learner who achieved 69% for Mathematics. (2)
1.4 Write down the correlation coefficient between the Mathematics and Physical Sciences marks for the data. (1)
1.5 Comment on the strength of the correlation between the Mathematics and Physical Sciences marks for the data.(1)
1.6 What trend did the teacher observe between the results of the two subjects?(1)
[10]
QUESTION 2
The number of aircraft landing at the King Shaka International Airport and the Port Elizabeth Airport for the period starting in April 2017 and ending in March 2018, is shown in the double bar graph below.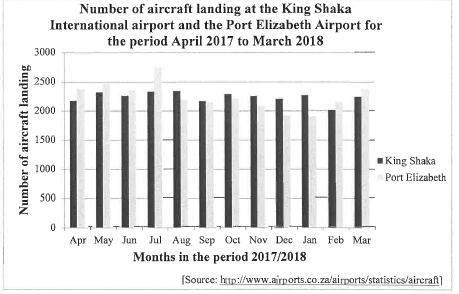
2.1 The number of aircraft landing at the Port Elizabeth Airport exceeds the number of aircraft landing at the King Shaka International Airport during some months of the given period. During which month is this difference the greatest? (1)
2.2 The number of aircraft landing at the King Shaka International Airport during these months are:
| 2182 | 2323 | 2267 | 2334 | 2346 | 2175 |
| 2293 | 2263 | 2215 | 2271 | 2018 | 2254 |
Calculate the mean for the data. (2)
2.3 Calculate the standard deviation for the number of aircraft landing at the King Shaka International Airport for the given period.(2)
2.4 Determine the number of months in which the number of aircraft landing at the King Shaka International Airport were within one standard deviation of the mean. (3)
2.5 Which ONE of the following statements is CORRECT?
- During December and January, there were more landings at the Port Elizabeth Airport than at the King Shaka International Airport.
- There was a greater variation in the number of aircraft landing at the King Shaka International Airport than at the Port Elizabeth Airport for the given period.
- The standard deviation of the number of landings at the Port Elizabeth Airport will be higher than the standard deviation of the number of landings at the King Shaka International Airport. (1)
[9]
QUESTION 3
ΔTSK is drawn. The equation of ST is y = ½x + 6 and ST cuts the x-axis at M. W(-4 ; 4) lies on ST and R lies on SK such that WR is parallel to the y-axis. WK cuts the x-axis at V and the y-axis at P(0 ; -4). KS produced cuts the x-axis at N. TSK = θ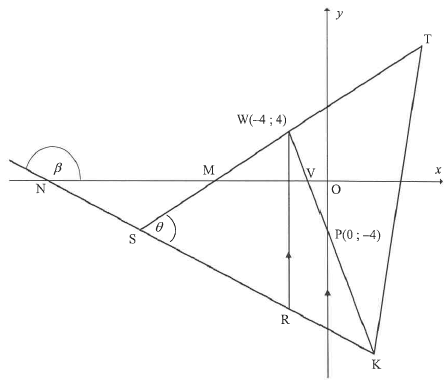
3.1 Calculate the gradient of WP.
3.2 Show that WP ⊥ ST.
3.3 If the equation of SK is given as 5y + 2x + 60 = 0, calculate the coordinates of S.
3.4 Calculate the length of WR.
3.5 Calculate the size of O.
3.6 Let L be a point in the third quadrant such that SWRL, in that order, forms a parallelogram. Calculate the area of SWRL.
QUESTION 4
M(-3 ; 4) is the centre of the large circle and a point on the small circle having centre 0 (0; 0). From N(-11 ; p) , a tangent is drawn to touch the large circle at T with NT is parallel to the y-axis. NM is a tangent to the smaller circle at M with MOS a diameter.
4.1 Determine the equation of the small circle.(2)
4.2 Determine the equation of the circle centred at M in the form (x - a)2 + (y - b)2 = r2 (3)
4.3 Determine the equation of NM in the form y = mx + c (4)
4.4 Calculate the length of SN. (5)
4.5 If another circle with centre B(-2 ; 5) and radius k touches the circle centred at M, determine the value(s) of k, correct to ONE decimal place.(5)
[19]
QUESTION 5
The graphs of f (x) = - ½-cos x and g(x)= sin(x +30°) , for the interval x∈ {0°;180°], are drawn below. A(130,9°; 0,33) is the approximate point of intersection of the two graphs.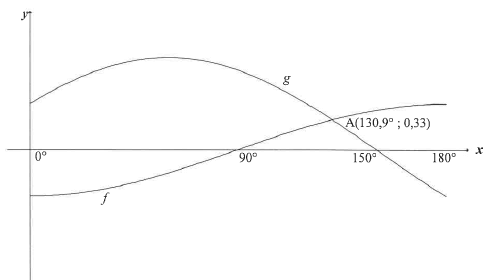
5.1 Write down the period of g. (1)
5.2 Write down the amplitude of f (1)
5.3 Determine the value of f (180°) - g(180°) (1)
5.4 Use the graphs to determine the values of x, in the interval x ∈ [0°; 180°], for which:
5.4.1 f (x - 10°) = g (x - 10°) (1)
5.4.2 √3 sinx + cosx ≥1 (4)
[8]
QUESTION 6
6.1 In the diagram, P(-5 ; 12) and T lies on the positive x-axis.POT = θ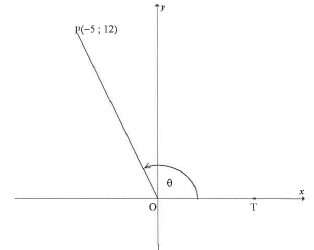
Answer the following without using a calculator:
6.1.1 Write down the value of tanθ
6.1.2 Calculate the value of cosθ
6.1.3 S(a ; b) is a point in the third quadrant such that TOS = θ +90° and OS = 6,5 units. Calculate the value of b.(4)
6.2 Determine, without using a calculator, the value of the following trigonometric expression:
sin 2x. cos(-x) + cos 2x. sin(360° - x)
sin(180° + x) (5)
6.3 Determine the general solution of the following equation:
6sin2 x + 7 cosx-3 = 0 (6)
6.4 Given: x + 1/x = 3 cos A and x2 + 1 = 2
x2
Determine the value of cos 2A without using a calculator. (5)
[24]
QUESTION 7
A landscape artist plans to plant flowers within two concentric circles around a vertical light pole PQ. R is a point on the inner circle and S is a point on the outer circle. R, Q and S lie in the same horizontal plane. RS is a pipe used for the irrigation system in the garden.
- The radius of the inner circle is r units and the radius of the outer circle is QS.
- The angle of elevation from S to P is 30°.
- RQS = 2x and PQ = √3r
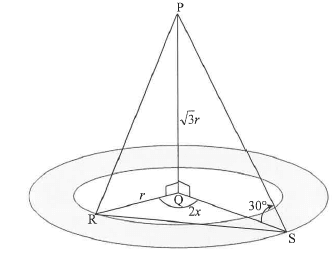
7.1 Show that QS = 3r
7.2 Determine, in terms of r, the area of the flower garden.
7.3 Show that RS = r √10 - 6 cos 2x
7.4 If r = 10 metres and x = 56°, calculate RS.
QUESTION 8
8.1 O is the centre of the circle.. KOM bisects chord LN and MNO = 26°. K and P are points on the circle with NKP = 32°. OP is drawn.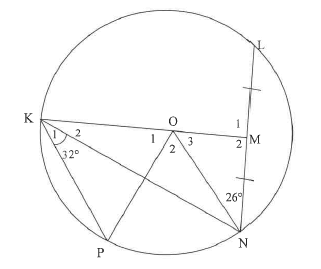
8.1.1 Determine, giving reasons, the size of:
- O2 (2)
- O1 (4)
8.1.2 Prove, giving reasons, that KN bisects OKP. (3)
8.2 In ΔABC, F and G are points on sides AB and AC respectively. D is a point on GC such that D1 = B.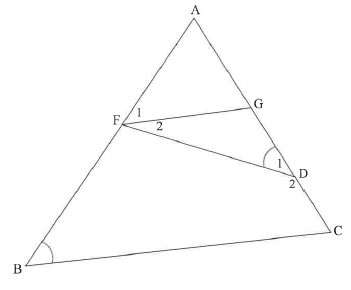
8.2.1 If AF is a tangent to the circle passing through points F, G and D, then prove, giving reasons, that FG II BC.(4)
8.2.2 If it is further given that AF/FB = 2/5 , AC = 2x - 6 and GC = x + 9, then calculate the value of x. (4)
[17]
QUESTION 9
9.1 In the diagram, 0 is the centre of the circle. Points S, T and R lie on the circle.
Chords ST, SR and TR are drawn in the circle. QS is a tangent to the circle at S.
Use the diagram to prove the theorem which states that Q ST = R.(5)
9.2 Chord QN bisects MNP and intersects chord MP at S. The tangent at P meets MN produced at R such that QN II PR. Let P1 = x .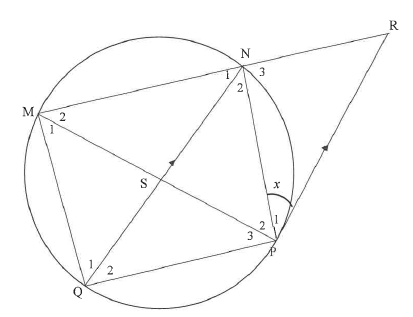
9.2.1 Determine the following angles in terms of x. Give reasons
- N2
- Q2
9.2.2 Prove, giving reasons, that MN/NR = MS/SQ
QUESTION 10
In the diagram, a circle passes through D, B and E. Diameter ED of the circle is produced to C and AC is a tangent to the circle at B. M is a point on DE such that AM I DE. AM and chord BE intersect at F.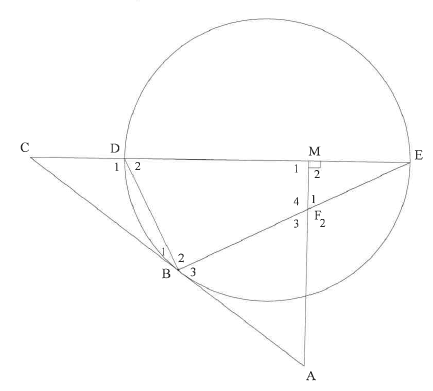
10.1 Prove, giving reasons, that:
10.1.1 FBDM is a cyclic quadrilateral (3)
10.1.2 B3 = F1 (4)
10.1.3 ACDB III ACBE (3)
10.2 If it is further given that CD = 2 units and DE = 6 units, calculate the length of:
10.2.1 BC(3)
10.2.2 DB (4)
[17]
TOTAL: 150
INFORMATION SHEET