TECHNICAL MATHEMATICS PAPER 1
GRADE 12
NATIONAL SENIOR CERTIFICATE
NOVEMBER 2020

INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of NINE questions.
2. Answer ALL the questions.
3. Answer QUESTIONS 4.1.2, 4.2 and 7.4 on the ANSWER SHEETS provided.
   Write your centre number and examination number in the spaces provided on the ANSWER SHEETS and hand in the ANSWER SHEETS with your ANSWER BOOK.
4. Number the answers correctly according to the numbering system used in this question paper.
5. Clearly show ALL calculations, diagrams, graphs, etc. that you have used in determining your answers.
6. Answers only will NOT necessarily be awarded full marks.
7. You may use an approved scientific calculator (non-programmable  and non- graphical), unless stated otherwise.
8. If necessary, round off answers to TWO decimal places, unless stated otherwise.
9. Diagrams are NOT necessarily drawn to scale.
10. An information sheet with formulae is included at the end of the question paper.
11. Write neatly and legibly.

QUESTION 1
1.1 The picture below shows a rectangular advertising board that consists of a frame and a rectangular area for placing an advertisement poster. (Note that the board is 3-dimensional.) The diagram next to the picture models the front view of the advertising board. The dimensions of the poster area are 12 metres by 3 metres. The frame has a uniform width of x metres, as shown in the diagram. The total front area of the rectangular board is 52 square metres.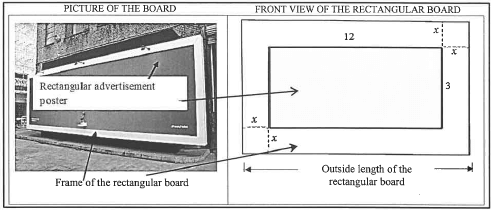

The following formula may be used:
Area of a rectangle = length x breadth
1.1.1 Write down the following in terms of x:

1. The outside length of the rectangular board(1)
2. The outside breadth of the rectangular board(1)

1.1.2 Show that the total front area (A)of the rectangular board can be expressed as A = 4x² +30x +36(2)
1.1.3 Hence, determine the outside length (in metres) of the rectangular board.(4)
1.2 Solve for x E {Real Numbers}:
1.2.1 ³/_x = 7x - 5 , x ≠ 0 (correct to TWO decimal places)(3)
1.2.2  x² + 4 > 0(1)
1.3  Solve for x and y if:  y - x = 3 and 3x² +xy - y² = - 3(6)
1.4 The following formula represents the relationship between capacitive reactance, frequency and capacitance: X_C =   1   
                                                                                                                                                                                           2πfC
Where: X_C = capacitive reactance (in ohms)
f  =  frequency (in hertz)
C = capacitance (in farads)
1.4.1 Express f as the subject of the formula.(1)
1.4.2 Hence,  determine, to the nearest  integer, the numerical value of f (in hertz) if X_c. = 63,66 ohms and C = 50 x 10^-6 farads.(2)
1.5 Given: 110011₂ and  111101₂
1.5.1 Determine the sum (in binary form) of the TWO binary numbers above. (1)
1.5.2 Hence, convert (clearly showing ALL calculations) the sum obtained in QUESTION 1.5.1 to its equivalent decimal number notation (2)
[24]

QUESTION 2
2.1 Given: 3x² + 2x + 2 = 0
2.1.1 Determine the numerical value of the discriminant ( A) of the equation (2)
2.1.2 Hence, describe the nature of the roots of the equation.(1)
2.2 Given: x² - 2p x = 3p² where p e {Real numbers}
2.2.1 Write the equation in the form axe + b x+ c = 0 (1)
2.2.2 Hence, without solving the equation, show that the roots of the equation are rational. (3)
[7]

QUESTION 3
3.1 Simplify the following WITHOUT using a calculator: 

3.1.1 log3 + log 27 (4)
          log81 - log9
3.1.2  2"√32 + 2"√2 (4)
               2"√50
3.2 Solve for x: log_x 32 + log_x 4 - log_x 16 = log₅125(5)
3.3 Two alternating-current circuits, connected in series, have impedances
Z₁ = 4 + 5i  and Z₂ = - 4 - 4i . The total impedance Z_T = Z₁ + Z₂
3.3.1 Calculate the total impedance Z_T  (1)
3.3.2 Hence, express the total impedance in the form ZT = r (cosθ+ isinθ)(4)
Show ALL calculations.
3.4 Solve for k and m  if  k = 6 + 4(i - 9) + 2mi(4)
[22]

QUESTION 4
4.1 Given functions f and  k  defined by  f (x) = - x + 4½  and  k (x) = √r² - x² respectively. Functions f and k have the same y-intercept.
4.1.1 Write down the length of the radius of k.
4.1.2 Sketch the graphs of f and k on the same set of axes provided on the ANSWER SHEET. Clearly show ALL intercepts with the axes.
4.1.3 Give the domain of k.
4.2 Sketch, on the axes provided on the ANSWER SHEET, the graph of function P defined by p(x) = ^-4/_x + q satisfying the following properties:

• x ≠ 0
• p(x) ≠ - 2
• p(-2) = 0

Clearly show the asymptoe(s) and the intercept(s) with the axes
4.3 The diagram below shows the graphs of functions g and h defined by g(x) = ax² + bx + 16  and  h (x) = k² + q  respectively.
P and U(2 ; 0) are the x-intercepts of g and R is the turning point of g.
T is the y-intercept of g.
V(-1 ; 8) is the point of intersection of the axis of symmetry of g and the asymptote of h.
S(1 ; 10) is the point of intersection of g and h.
W is the point of intersection of h and the axis of symmetry of g.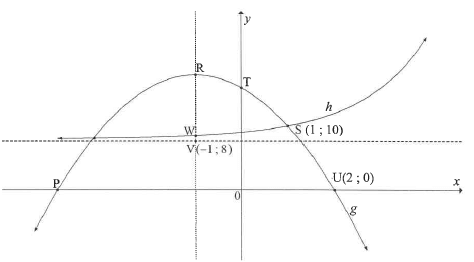

4.3.1 Write down the coordinates of:

1. T(1)
2. P(2)

4.3.2 Determine the numerical value(s) of a and b. (4)
4.3.3 Determine the y-coordinate of R. (2)
4.3.4 Show that h(x) = 2X + 8 (3)
4.3.5 Write down the range of h. (1)
4.3.6 Determine the length of VW. (3)
[27]

QUESTION 5
5.1 An artisan wants to buy a car after seeing the advertisement alongside.

5.1.1 Determine the loan amount that the artisan had to take out for this deal.(1)
5.1.2 Calculate, correct to ONE decimal place, the annual effective interest rate. (3)
5.2 An engineering company conducted an audit of the number of its unskilled workers during March 2019.
Due to the Fourth Industrial Revolution (4IR), it is estimated that by April 2023, the number of unskilled workers employed by the company will decrease at a compound rate of 5,43% per annum, to 60 unskilled workers.
Calculate how many unskilled workers were employed by the engineering company during April 2019. Show ALL calculations. (4)
5.3 Bongi received a bonus of R85 000 and decided to invest the bonus for a period of 6 years. The interest rate for the first two years was 5,4% per annum, compounded semi-annually, and for the remaining years changed to 6% per annum, compounded monthly. At the end of the 4th year, he withdrew  R20 000  from the investment account to pay his daughter's school fees.
5.3.1 Calculate the value of the investment at the end of the first two years. (2)
5.3.2 Hence, determine whether the final amount that Bongi will receive at the end of the investment period, will be more than the amount he originally invested. (6)
[16]

QUESTION 6
6.1 Determine f ^l(x) using FIRST PRINCIPLES if f (x) = ½x (4)
6.2 Determine EACH of the following:
6.2.1 dA  if  A = πr² (1)
         dr
6.2.2  D_x[(x - √x)²(5)
6.3 The equation of a tangent to the curve of function  g  defined by g(x)= ax² - x is 3x - y + 2 = 0
The point of contact of the tangent and the curve of g is  ( -1; -1) . Determine the numerical value of a. (5)
[15]

QUESTION 7
Given: Function f defined by f (x) = -(x -1)² (x + 3) = -x³ - x² + 5x - 3
7.1 Write down the y-intercept of f(1)
7.2 Determine the x-intercepts of f (2)
7.3 Determine the coordinates of the turning points of f (5)
7.4 Sketch the graph of f on the ANSWER SHEET provided. Clearly show ALL the intercepts with the axes and the turning points. (4)
7.5 Determine the values of x for which f ^/(x) > 0  (2)
[14]

QUESTION 8
8.1 The distance   (D), in metres, covered by a car in t seconds, before reaching a certain point on a straight road, is given by the equation  D(t)= - 0,5 t² + 20 t
Determine:
8.1.1 The distance covered by the car in t = 10 seconds (1)
8.1.2 The velocity of the car where t = 12 seconds (3)
8.2 The diagram below represents a wooden block in the shape of a triangular right prism.
The right-angled triangular faces have side lengths 3x cm,  4x cm and 5x cm.
The height of the wooden block is y cm.
The total surface area of the wooden block is 3 600 cm².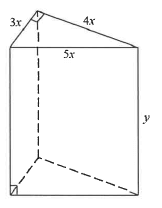

The following formulae may be used:
Volume of a right prism = (area of base) x height
Total surface area of a right prism = 2 x (area of base) + (perimeter of base) x height
8.2.1 Show that:

1. The height (in cm) of the block is represented by:
   y = 300 - x² 
             x          (3)
2. The volume (in cm³) of the block is represented by:
   V = 1 800x - 6x³
   

8.2.2 Hence, calculate the value of x  that will maximise the volume of the block.

QUESTION 9
9.1 Determine the following:
9.1.1  ∫2^xdx(2)
9.1.2 ∫(√x + ⁷/_x + 4x^-5 )dx(4)
9.2 The sketch below represents function f  defined by  f (x) = - x² - x + 6, with x-intercepts at (- 3 ; 0) and (2 ; 0).
The shaded area, bounded by the curve and the x-axis between the points  x = -1 and x = 1,  is shown in the sketch.
The area of the shaded part is ³⁴/₃ square units.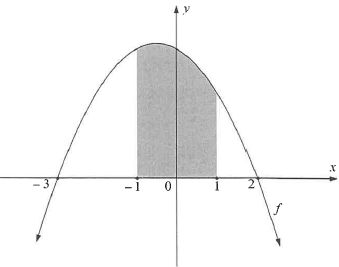

Determine whether the unshaded area, bounded by the curve and the x-axis between the points x = - 3 and x = 2,  is less than the shaded area.(7)
TOTAL:150

INFORMATION SHEET: TECHNICAL MATHEMATICS