INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of 11 questions. Answer ALL the questions.
2. Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
3. Answers only will NOT necessarily be awarded full marks.
4. You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
5. If necessary, round off answers to TWO decimal places, unless stated otherwise.
6. Diagrams are NOT necessarily drawn to scale.
7. An information sheet, with formulae, is included at the end of the question paper.
8. Number the answers correctly according to the numbering system used in this question paper.
9. Write neatly and legibly.

QUESTIONS

QUESTION 1
1.1 Solve for x, in each of the following:
1.1.1 2x ( x +1) = 0  (2)
1.1.2  2x(x - 3) =1   (correct to TWO decimal places)  (4)
1.1.3  x² - 2x -15 ≤ 0  (3)
1.1.4
(3)
1.2 Solve simultaneously for x and  y in the following equations:
x - 2 y = 3
4x² - 5xy = 3 - 6 y       (6)
1.3 The equation 3mx² - px + 5 = 0 ; m # 0 and p # 0 , has equal roots.
1.3.1 Show that f (x) = 3mx² - px + 5 has a minimum value. (4)
1.3.2 If it is further given that p < 0 , draw a sketch graph of f (x) = 3mx² - px + 5 . (2)
[24]

QUESTION 2
2.1 Determine which term of the sequence: 23; 21; 19; . . . is - 47. (2)
2.2 The first three terms of an arithmetic sequence are: 3x - 1 ; x + 5 ; 2x - 4
2.2.1 Calculate the value of x. (3)
2.2.2 Determine the number of terms of which the sum is equal to zero. (4)
2.3 Given the quadratic pattern: 25 ; 48 ; 69 ; 88 ; x ; y ; . . . Determine:
2.3.1 The values of x and y (2)
2.3.2 The general term, Tn of the quadratic pattern (4)
2.3.3 The value of the largest term of this pattern (3)
2.4 Calculate the value of a, if: 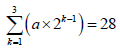   (2)
[20]

QUESTION 3
A circular disk of radius, R is cut out of paper as shown in the diagram. Two disks of radius, ½R are cut out of paper and placed on top of the first disk, as shown. Then four disks of radius, ¼R are cut out of paper and placed on top of the two disks, as shown.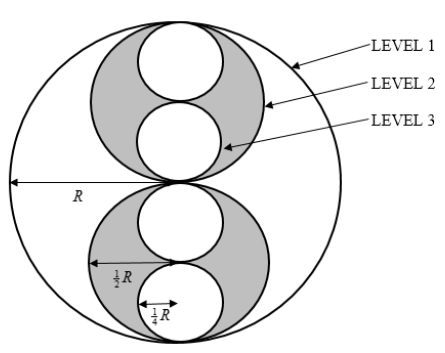

3.1 If this process can be repeated, determine the area of the disks on the fourth level only. (4)
3.2 Calculate the total area of all the disks, if the process is repeated indefinitely. (3)
[7]

QUESTION 4
Given: f (x) = -x² - 4x + 5 and g(x) = ax + q. E, M and P are the intercepts of the graphs with the axes. N is the turning point and NTD the axis of symmetry of f . T is a point on the graph of g and S is the reflection of M about the axis of symmetry.

Determine:
4.1 The coordinates of M, E and P (4)
4.2 The coordinates of N (3)
4.3 The values of a and q (2) 
4.4 The length of NT (3) 
4.5 The equation of the tangent to f at point S (5)
[17]

QUESTION 5
In the figure below, two sketch graphs are shown for: f (x) = ^k/_x , where x > 0 and g(x) = log _p x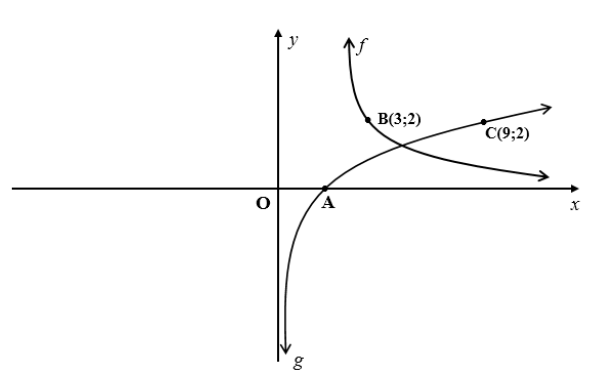

5.1 Write down the coordinates of A. (1)
5.2 Determine the values of k and p. (3)
5.3 Determine the equation of g ^-1 in the form y = ... (2)
5.4 Write down the range of g ^-1 . (2)
5.5 Solve for x if 6 - log₃x = 1   (2)
                           x   

[10]

QUESTION 6
Given: g(x) = (x + 2)(y + 3) = k ; for k > 0 , is a hyperbola with g(0) =- ⁵/₂ . Determine:
6.1 The equations of the asymptotes of g (3)
6.2 The value of k (2) 
6.3 The equation of the axis of symmetry of g which has a negative gradient (2)
[7]

QUESTION 7
7.1 Convert a nominal interest rate of 8,9% a. compounded monthly to effective interest rate per annum.      (3)
7.2 Alan retires and decides to invest R1 000 000 of his retirement lump sum. The bank offers him an interest rate of 12,6% a. compounded monthly. How long will it take for his money to double?   (4)
7.3 R60 000 is invested in an account which offers interest at 7% a. compounded quarterly for the first 18 months. Thereafter the interest rate changes to 5% p.a. compounded monthly. Three years after the initial investment, R5 000 is withdrawn from the account. How much money will be in the account at the end of 5 years?  (7)

[14]

QUESTION 8
8.1 Given  f (x) = -7x². Determine f'(x) from first principles.  (4)
8.2 Determine dy  if:
                       dx
8.2.1 y = 1 + √x   (3)
              x⁴

8.2.2 y =  x - 4   (3)
              x^½ - 2

[10]

QUESTION 9
Given: g(x) = x³ + x² -16x + 20
9.1 Show that (x +5) is a factor of g(x).  (2)
9.2 Hence, or otherwise determine the x-intercepts of g. (3)
9.3 Determine the coordinates of the turning points of g. (4)
9.4 Sketch the graph of g(x), showing clearly the intercepts with the axes and the turning points. (3)
9.5 Discuss the concavity of the graph at the y-intercept. Support your answer with relevant (3)
9.6 For which values of x will x. f'(x) ≥ 0?  (3)
[18]

QUESTION 10
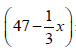The total cost of producing x cellphones per day is given by rand and each cellphone is sold for a price of rand.
10.1 Determine an expression for money raised from the sale of x (2)
10.2 How many cellphones should be made daily to maximise the profit? (5)
[7]

QUESTION 11
11.1 Given:

• P(A) = 0,5
• P(A and B) = 0, 2
• P(not B) = 0,6

11.1.1 Determine P(A or B) (3)
11.1.2 Your teacher claims that events A and B are independent. Do you agree or disagree? Justify your answer with (3)
11.2 A bag contains five red and y green marbles.
11.2.1 What is the probability that a red or a green marble will be drawn from the bag?  (1)
11.2.2. Two marbles are drawn successively without Represent this using a tree diagram. Label all the branches and write down the outcomes. (4)
11.2.3 Determine how many green marbles are in the bag if the probability of drawing two marbles of the same colour is ³¹/₆₆ .(5)
[16]

TOTAL:    150

INFORMATION SHEET: MATHEMATICS