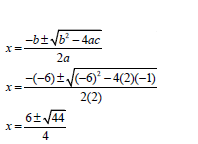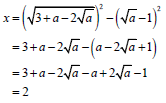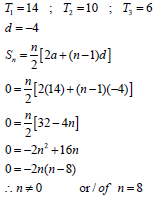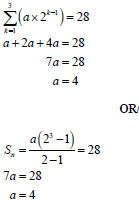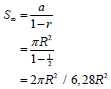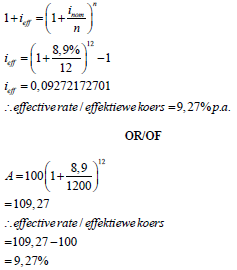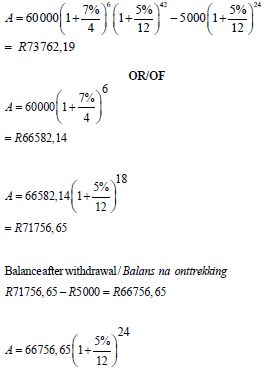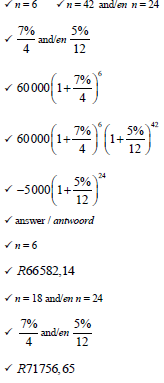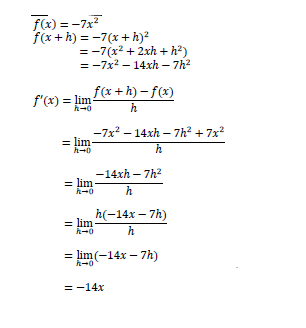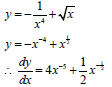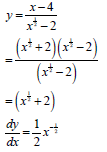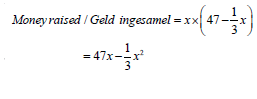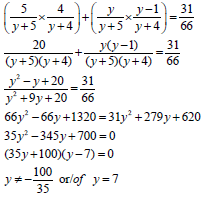QUESTION 1

1.1.1

2x(x +1) = 0
2x = 0 or x +1 = 0
x = 0 or   x = -1

x = 0
x = – 1      (2)

1.1.2

2x(x - 3) = 1  Penalise 1 mark for incorrect rounding off.
2x² - 6x - 1 = 0 

∴ x = 3,16      or      x = -0,16

standard form 
substitution 
√√ 𝑥-values    (4)

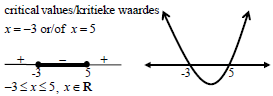
1.1.3

x2 - 2x - 15 ≤ 0
(x + 3)( x - 5) ≤ 0
critical values

OR
x ∈[-3 ; 5]  , x ∈ R

factors 
√√ -3 ≤ x ≤ 5 (accuracy)

OR

x ∈[-3 ; 5]  (3)

1.1.4

3 + a - 2√a
a - 2√a + 1
answer 

(3)

1.2

x - 2 y = 3 .......................(1)
4x² - 5xy = 3 - 6y ........................(2)
From (1) :  x = 2 y + 3 ................ (3)
(3) into (2) : 4(2y + 3)² -  5y(2y + 3) = 3 - 6y
4(4y² + 12y +  9)- 10y² - 15y - 3 + 6y = 0
16y² + 48y + 36 - 10y² - 15y - 3 + 6y = 0
6y² + 39y + 33 = 0
(6y + 33)(y + 1) =  0
y = -33 or  y =  -1
        6
y = -11
        2
x = - 8 or x = 1

x = 2y + 3
substitution
standard form 
factors 
𝑦-values 
x-values 

1.3.1

For equal roots Δ = 0
b² - 4ac = 0
(-p)² - 4(3m)(5) = 0
p² - 60m = 0
p² = 60m
∴ m > 0 ⇒ 3m > 0
∴ minimum value

Δ = 0
substitution and simplification
p² = 60 m
conclusion

(4)

1.3.2

Consider axis of symmetry
x = -b = -(+) = -ve
      2a  2(+)

method 
correct sketch 

(2)

[24]

QUESTION 2

2.1

23 ; 21 ; 19 ; . . . ; – 47
a = 23 and d = –2
T_n = a + (n - 1)d
-47 = 23 + (n - 1)(-2)
-47 = 25 - 2n
2n = 72
n = 36

substitution 
answer 

(2)

2.2.1

T₂ - T₁ = T₃ - T₂
(x + 5) - (3x -1) = (2x - 4) - (x + 5)
x + 5 - 3x + 1 = 2x - 4 - x - 5
-2x + 6 = x - 9
15 = 3x
∴x = 5

method 
substitution 
answer 

(3)

2.2.2

first term and common difference
substituting S_n , a and d
standard form 
answer 

2.3.1

25 ; 48 ; 69 ; 88 ; x ; y
1^st difference pattern :
23 ; 21 ; 19 ; 17 ; 15...
∴ x = 105 and y = 120

√ x = 105      
√ y = 120

(2)

2.3.2

2a = -2          3a + b = 23             a + b + c = 25
a = -1            3(-1) + b = 23         (-1) + (26) + c = 25
b = 26              c = 0
∴ T_n = -n² + 26n

value of a 
value of b 
value of c 
answer 
(√√√√ can be awarded at formula)

2.3.3

n = -b
     2a
T₁₃ = -(13)² + 26(13)

= -(26)       = 169
   2(-1)
= 13

method 
n = 13
answer  (T₁₃ = 169)

(3)

2.4

answer 
substitution 
answer 

[20]

QUESTION 3

3.1

A_level1 =  1 × πR²
A_{level 2} =  2 × π(½R)²  = ½πR²
A_{level 3} =  4  × π(¼R)²  = ¼πR²
A_{level 4} =  8  × π(¹/₈R)²  = ¹/₈πR² / 0,39R²

OR 

a = πR² ; r = ½
T₄ = (πR²)(½)³ = ¹/₈πR² / 0,39R²

OR

A_{level 4} =  8  × π(¹/₈R)² 
= ¹/₈πR² / 0,39R²

substitution
answer 
If this option is given:
√ 8
√ ¹/₈R
√√ answer

(4)

(4)

3.2

formula 
substitution
answer 

(3)

[7]

QUESTION 4

4.1

-x² - 4x + 5 = 0
x² + 4x - 5 = 0
(x + 5)(x -1) = 0
x = -5 or  x = 1
M(0 ; 5)
E(-5 ; 0)
P(1 ; 0)

solving for x-intercepts
M(0 ; 5)
E(-5 ; 0)
P(1 ; 0)

(4)

4.2

x = (-5 + 1) = -2      or    x = -(-4) = -2
         2                                2(-1)
y = -(-2)² - 4(-2) + 5 = 9
∴ N (-2;9)

x-value 
substitution 
y-value 

(3)

4.3

a = 1    and  q = 5

a = 1
q = 5

(2)

4.4

Length of ND = 9 (from 4.2)
y = x + 5
= -2 + 5
= 3
∴ length of TD = 3
NT = ND – TD
= 9 – 3
= 6

ND = 9

TD = 3

NT = 6

4.5

m = f'(-4)
= -2(-4) - 4
= 4
y - 5 = 4(x - 4)
y = 4x + 21

coordinates of S 
m = f'(-4)
m = 4
substitution 
answer 

[17]

QUESTION 5

5.1

A(1 ; 0)

answer 

(1)

5.2

f (x) = k
          x
2 =  k
       3
k = 6

g(x) = log p x

2 = log_p 9
p₂ = 9 ⇒ p = 3

p² = 9
p = 3

5.3

y = log₃x
g ^-1 : x = log₃y
∴ y = 3^x
Answer only: Full marks

interchanging x and y
answer 

(2)

5.4

Range of g ^-1
y > 0 ; y ∈ R

√√ answer 

(2)

5.5

6 = log₃x + 1
x  
(3 ; 1) will be a point on g
g(x) + 1 will intersect f at (3 ; 2) 
∴ x = 3

(3 ; 1) point on g 
answer

(2)

[10]

QUESTION 6

6.1

g(x) = (x + 2)( y + 3) = k
( y + 3) =        k             
                   (x + 2)
y =      k          - 3
       (x + 2)
x = -2 (vertical asymptote)
y = -3 (horizontal asymptote)

standard form 
x = -2
y = -3

(3)

6.2

substitution 
answer 

(2)

6.3

y = -(x + 2) - 3
y = -x - 5

substitution 
answer 

(2)

[7]

QUESTION 7

7.1

substitution 
answer

formula
substitution 
answer

(3)

(3) 

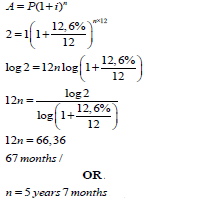substitution 

use of logs 

solving for n 

answer 

(4)

= R73762,18
Penalise 1 mark for incorrect notation in the question

subtraction
final answer

QUESTION 8

8.1

Answer only = 0 marks

−7𝑥² − 14𝑥ℎ − 7ℎ²
substitution
simplification
answer   (4)

8.2.1

√ x^-4 + x^½
√  4x^-5   √ ½ x^-½   (3)

8.2.2

(x^½ + 2)(x^½ - 2)
simplification
answer         (3)

[10]

QUESTION 9

9.1

g(-5) = (-5)³ + (-5)² -16(-5) + 20
= -125 + 25 + 80 + 20
= 0
∴ (x + 5) is a factor 

substitution 
answer

(2)

9.2

g(x) = x³ + x² -16x + 20
= (x + 5)(x² - 4x + 4)
= (x + 5)(x - 2)(x - 2)
∴ x = -5 or  x = 2 or  x = 2

(x² - 4x + 4)
(x - 2)(x - 2)
x-intercepts 

(3)

9.3

g'(x) = 3x² + 2x -16 = 0
(3x + 8)(x - 2) = 0
3x + 8 = 0 or x - 2 = 0
x = - 8 or  x = 2
        3
y = 50,81 or  y = 0

g'(x)
factors 
x-values 
y-values 

(4)

9.4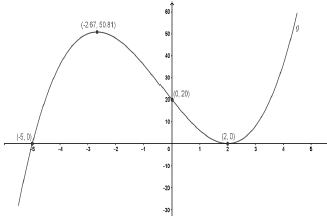

intercepts with the axes
turning points 
shape

9.5

g''(x) = 6x + 2
g''(0) = 6(0) + 2
= 2 > 0
∴ concave up / konkaaf opwaarts

OR 

g''(x) = 6x + 2 = 0
x = - ¹/₃  (x-coordinate of  point of inflection)
but :0 > -¹/₃ ⇒  concave up tothe right of - ¹/₃

g''(x)

substitution 

conclusion 

g''(x)

x = - ¹/₃

conclusion

(3)

9.6

OR

-⁸/₃ ≤ x ≤ 0  or  x ≥ 2

(3)

[18]

QUESTION 10

10.1

multiplication
answer

(2)

10.2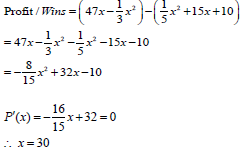

method 
substitution and simplification
answer 
P'(x) = 0
answer 

[7]

QUESTION 11

11.1.1

P( A or B) = P( A) + P(B) - P( A and B)
= 0, 5 + 0, 4 - 0, 2
= 0, 7

P(B) = 0,4
substitution
answer 

(3)

11.1.2

P( A and/en B) = 0, 2
P( A) ×  P(B)
= 0, 5 × 0, 4
= 0, 2
∴ Agree  :  P( A and B) = P( A) × P(B)

P(A) x P(B) = 0,2
answer 
reason 
(Use of independent rule)

11.2.1

P(R or G) = 1 OR (100%)

answer 

(1)

11.2.2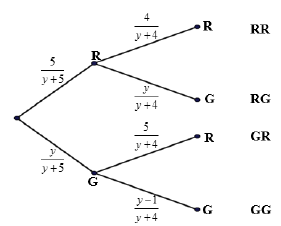

first branch with labels

second branch with labels

third branch with labels

outcomes 

(4)

11.2.3

method 
multiplying 
standard form 
factors 
answer 

[16]

TOTAL:

150