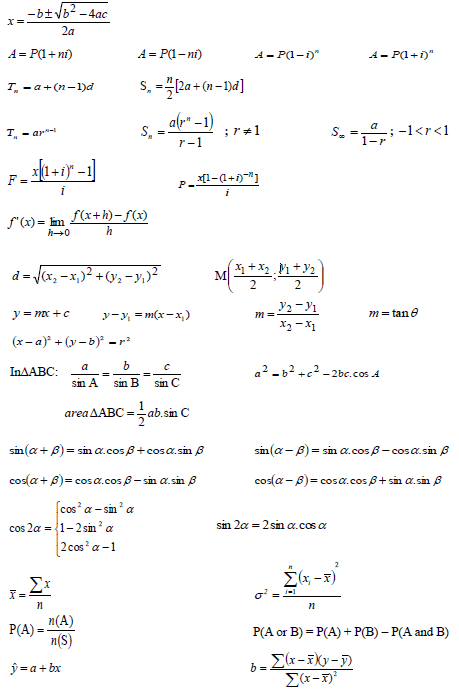Mathematics Paper 2 Questions - Grade 12 June 2021 Exemplars
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupINSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.
- This question paper consists of 11 questions.
- Answer ALL the questions in the ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in determining your answers.
- Answers only will NOT necessarily be awarded full marks.
- You may use an approved scientific calculator (non-programmable and non-graphical), unless stated otherwise.
- If necessary, round off answers to TWO decimal places, unless stated otherwise.
- Diagrams are NOT necessarily drawn to scale.
- An information sheet with formulae is included at the end of the question paper.
- Write neatly and legibly.
QUESTIONS
QUESTION 1
The box and whisker diagram below represents soccer clubs’ standings from position 1 to 14 after playing an equal number of games.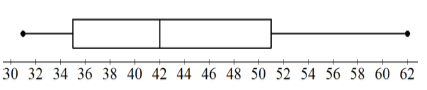
The following table is partly completed, from top (position 1) to bottom (position 14):
Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Points | a | 59 | 58 | b | 49 | 45 | c | 42 | 37 | 36 | d | 32 | 32 | e |
1.1 Write down the values of a, b, c, d and e. (5)
1.2 Comment on the skewness of the data. (1)
1.3 One commentator says the top four teams each had at least 50 points. Do you agree with the commentator or not? Justify your answer. (2)
[8]
QUESTION 2
A school organised a weekend camp for the 90 grade 12 learners doing Mathematics. Learners wrote a pre-test (test before classes started) and a post-test (test after classes finished), out of 50 marks. Below is the graph representing the data.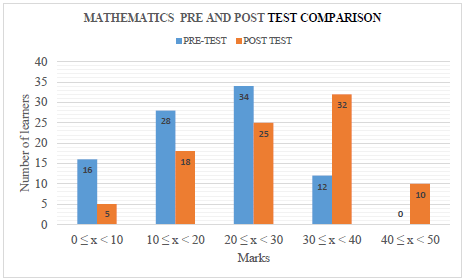
2.1 Use the graph to conclude whether the camp had a positive impact (improved performance) or not. Give a reason for your answer. (2)
2.2 Write down the modal class of pre-test marks. (1)
2.3 Is the mean mark of the pre-test greater than, less than or the same as that of the post-test? (1)
2.4 Complete the frequency and cumulative frequency table in the ANSWER BOOK.
| Marks | Frequency | Cumulative Frequency | ||
| Pre-test | Post-test | Pre-test | Post-test | |
| 0 ≤ x < 10 | ||||
| 10 ≤ x < 20 | ||||
| 20 ≤ x < 30 | ||||
| 30 ≤ x < 40 | ||||
| 40 ≤ x < 50 | ||||
(4)
2.5 Draw the cumulative frequency graphs (ogives) using the grid provided in the ANSWER BOOK. (3)
2.6 The teacher targeted to have 50% more learners to get 60% or more in post-test compared to pre-test. Determine, with the necessary calculations or justification, whether the teacher achieved the target or not. (3)
[14]
QUESTION 3
∆RPQ with vertices R(2; 6), P (– 5; 0) and Q(t; – 4) is given below. RQ is perpendicular to the x-axis and cuts the x-axis at S. O is the origin.
3.1 Write down the value of t. (1)
3.2 Determine:
3.2.1 the length of PR. Leave your answer in simplest surd form. (2)
3.2.2 the gradient of PR. (2)
3.3 Determine the size of PRQ . (5)
3.4 Determine whether ΔQPR is right angled at P or not. (4)
3.5 Determine the equation of the line parallel to PQ and passing through the origin. (3)
3.6 Determine the value of Area of ΔSPR (5)
Area of ΔPRQ
[22]
QUESTION 4
In the diagram below, the smaller circle with diameter KM passing through centre L has a tangent at M and y-intercept at N. The equation of the smaller circle is
x2 + y2 + 6x - 6y + 9 = 0
The bigger circle passes through M. The origin, O and K (– 5 ; 5) is given.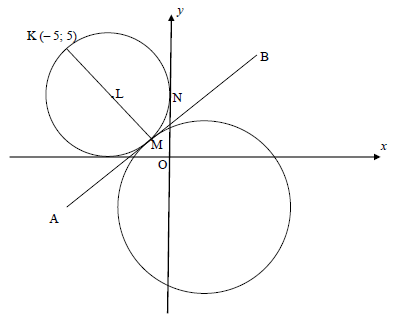
4.1 Determine:
4.1.1 the coordinates of L and the length of the radius of the smaller circle (4)
4.1.2 the coordinates of M (3)
4.1.3 the equation of tangent AMB in the form y = …. (4)
4.1.4 the coordinates of N (2)
4.2 If the coordinates of the centre of the bigger circle is a result of shifting the coordinates of L, 5 units to the right and 7 units down.
4.2.1 Write down the coordinates of the centre of the new circle. (2)
4.2.2 Determine whether the diameter of the bigger circle from a common point of contact M passes through the origin or not. (4)
[19]
QUESTION 5
5.1 Given that sin ∝ = - 5/13 and tan ß = - 3/4 where ∝, ß ∈[90º ;270º] , calculate, without the use of a calculator, the value of:
5.1.1 sin (∝+ ß) (5)
5.1.2 cos 2ß (3)
5.1.3 tan (– ∝ – 180⁰ ) (2)
5.2 Consider the identity:
sin θ - cos θ = 1
1 - cos θ sin θ sin θ
5.2.1 For which value(s) of θ , for θ∈[0º;360º] is the identity undefined? (2)
5.2.2 Prove the identity. (4)
5.3 If tan x = 3k and tan y = 2k, determine sin (x - y) in terms of k (4)
cos x.cos y
[20]
QUESTION 6
Given the functions:
f (x) = cos(x - 60º) and g(x) = sin3x for x∈[ -90º;180º]
6.1 Write down:
6.1.1 the amplitude of f (1)
6.1.2 the period of g (1)
6.2 Determine the values of x for which f(x) = g(x) for x ∈ [– 90° ; 180°] (6)
6.3 On the same set of axes, sketch the graph of f and g for x ∈[–90°; 180°] in the SPECIAL ANSWER BOOK. Show ALL intercepts with the axes as well as turning and end points. (5)
6.4 For which value(s) of x is g(x)/f(x) undefined for x ∈[–90°; 180°]? (1)
6.5 Write down the equation of h(x) if h(x) is a result of shifting f(x), 15⁰ to the left. (1)
[15]
QUESTION 7
The diagram below shows ΔABC with lengths 5, 5 and 4 units.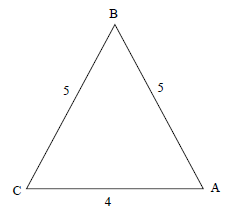
Determine the numerical value of cos A-cos B (5)
[5]
Give reasons for your statements in QUESTIONS 8, 9, 10 and 11.
QUESTION 8
In the diagram below, O is the centre of circle A, B, C and D. M is the midpoint of chord CD. Line OM is drawn. AB is the diameter. AB = 22 cm and OM = 7 cm.
Determine, with reasons, the length of CD. (5)
[5]
QUESTION 9
In the diagram below, a bigger circle PQRST intersects a smaller circle at R and S. VW is a tangent of the smaller circle at U. SUQ and TUR are straight lines.
Chords RQ, QP, PT, QT, TS and SR are also drawn. RTQ = x .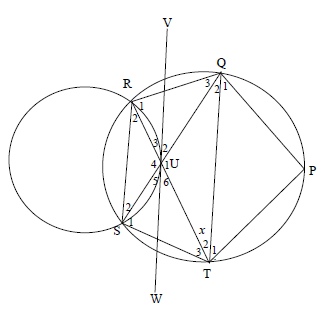
9.1 Prove, with reasons, that ΔRUS ||| ΔQUT. (3)
9.2 Determine, with reasons, THREE other angles each equal to x. (4)
9.3 If RQT = 90° – x , determine :
9.3.1 whether QT is a diameter or not. (4)
9.3.2 P (2)
9.4 If it is further given that UQ = UT, show that:
9.4.1 RS || QT (2)
9.4.2 VW is also a tangent to the circle passing through QUT at U. (2)
[17]
QUESTION 10
10.1 In the diagram below, O is the centre of circle FGH with DG a tangent at G.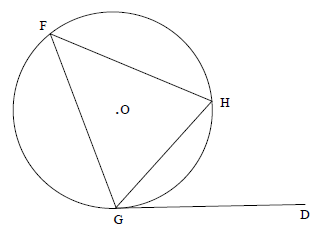
Prove the theorem which states that DGH = F. (5)
10.2 In the diagram below, O is the centre of circle LMP with tangents KL and KP at L and P respectively. OLM = 67º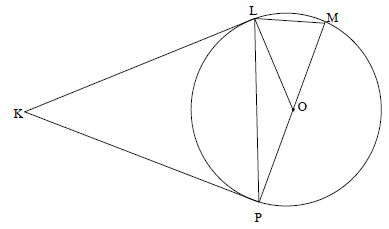
10.2.1 What type of quadrilateral is KLOP? (1)
10.2.2 Give, with reasons, 3 angles each equal to 90°. (5)
10.2.3 Prove, stating reasons, that KLOP is a cyclic quadrilateral. (2)
10.2.4 Hence, determine K . (5)
[18]
QUESTION 11
In the diagram below, ∆ABC is drawn with PQ || BC and RS || AC.
AQ : QC = 3 : 5 and BR : RA = 1 : 3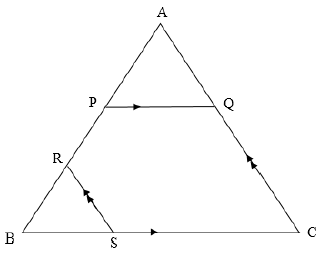
Prove that AP = PR. (7)
[7]
TOTAL: 150
INFORMATION SHEET: MATHEMATICS