INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of NINE questions. Answer ALL the questions.
2. Clearly show ALL calculations, diagrams, graphs, et cetera, which you have used in determining your answers.
3. An approved scientific calculator (non-programmable and non-graphical) may be used, unless stated otherwise.
4. If necessary, ALL answers should be rounded off to TWO decimal places, unless stated otherwise.
5. Number the answers correctly according to the numbering system used in this question paper.
6. Diagrams are NOT necessarily drawn to scale.
7. An information sheet with formulae is attached.
8. Answer QUESTION 4.2.5 and QUESTION 7.5 on the ANSWER SHEETS provided. Write your name in the space provided and hand in the ANSWER SHEETS with your answer book.
9. Write neatly and legibly.

QUESTIONS

QUESTION 1
1.1 Solve for x:
1.1.1 x² - 8x - 33 = 0 (3)
1.1.2 x² - 7x = 10 (-3x+1) (correct to TWO decimal places)  (3)
1.1.3 -2x² + 9x + 5 < 0 (4)
1.2 The diagram below is a rectangle with perimeter equal to 90 cm.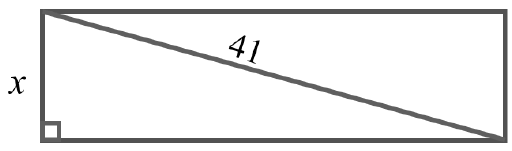

The following formula may be used: Perimeter of a rectangle = 2 (l + w)
Determine the width (x) of the rectangle if the diagonal is 41 cm. (6)
1.3 Solve for x and y simultaneously given that:
x = y+ 3 and y - x² = -2x - 3 (5)
1.4 Given: K = (1× 2³ ) + (1× 2⁵) + 2⁰
1.4.1 Simplify K. (1)
1.4.2 Hence, write K in binary form. (1)
[23]

QUESTION 2
2.1 Given: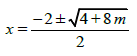

Determine the value(s) of m for which the roots will be non-real. (2)
2.2 Determine the nature of roots of ax² - bx - ¹/_a = 0; a # 0; a,b∈Q , given that b = 0. (4)
[6]

QUESTION 3
3.1 Simplify the following WITHOUT using a calculator:
3.1.1  (2)
3.1.2 log√65 + log√260 - log13 (4)
3.2 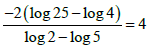(3)
3.3 Solve for x:
3.3.1 (3)
3.3.2 log₃(x - 3) - log₃ 5 =1 (3)
3.4 Determine the numerical values of x and y if x - 3(5i + 2) = 4 - 3i + yi .  (3)
3.5 Convert V = 110, 4 + 46,1i to polar form. (5)
[23]

QUESTION 4
4.1 In the diagram below, the graphs of g and h are defined by and h (x) = ^a/_x respectively. The point of intersection of g and h is A (1;3).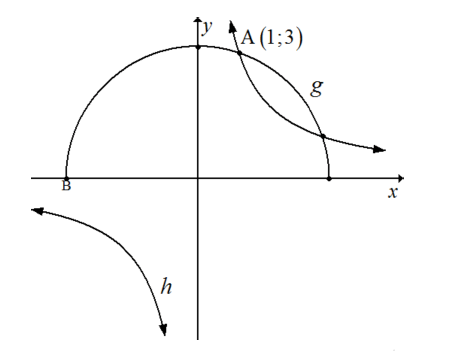

Determine:
4.1.1 The value(s) of a and r (3)
4.1.2 The range of g (2)
4.1.3 The coordinates of point B (1)
4.1.4 The equation of the asymptotes of h (2)
4.2 Given the functions f and k defined by f (x) = 2^x and k(x) = 2( x - 2)² - 2.
4.2.1 Determine the y-intercept of k (2)
4.2.2 Write down the coordinates of the turning point of k (2)
4.2.3 Determine the x-intercepts of k (4)
4.2.4 Write down the domain of f (1)
4.2.5 Sketch the graphs of f and k on the same set of axes on the ANSWER SHEET provided. Clearly show the asymptotes, intercepts with the axes and the coordinates of any turning points. (6)
4.2.6 Write down the range of k. (1)
[24]

QUESTION 5
5.1 Sam hired an angle grinder, as shown in the picture below, at a tool hire shop at a flat rate of 15% per hour plus R35.
Determine how much it will cost to hire the angle grinder for 9 hours.
(2)

5.2 The present population of a small town is 13 565. It is stated that the population grows annually at a compound growth rate of 6,5%. Determine the population size of this town after 8 years. (3)
5.3 Linzo deposited R 120 000,00 in an investment account. She further deposited R50 000,00 into the same account after 12 months. She withdraws R35 000,00 from the same account to pay for repairs to the roof of her house at the end of 2 years.

• The interest rate during the first year is 9% p.a. compounded monthly.
• Thereafter, the interest rate is changed to 8,5% p.a. compounded quarterly.

Calculate the balance of the account after 5 years.(8)
[13]

QUESTION 6
6.1 Determine f'(x) by using FIRST PRINCIPLES if f (x) = -2x+ ¼ (5)
6.2 Determine the following:
6.2.1 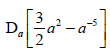 (2)
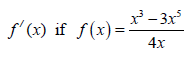6.2.2 (3)
6.2.3 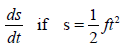 where f is a constant and f = π (2) 
6.3 Determine the numerical x-value between 2 and 8 such that the instantaneous rate of change of f (x) = 3x² is equal to the average rate of change over the interval x ∈[2;8]. (4)
[16]

QUESTION 7
Given: g(x) = x³ - 12x - 16
7.1 Show that ( x + 2) is a factor of g. (2)
7.2 Determine the x-intercepts of g. (4)
7.3 Write down the coordinates of the y-intercept of g. (1)
7.4 Determine the coordinates of the turning points of g. (6)
7.5 Sketch the graphs of g on the ANSWER SHEET provided. Show clearly the intercepts with the axes and the coordinates of any turning points. (4)
7.6 Without simplifying the equation, determine the defining equation of h if g (x) is shifted so that the local maximum coincides with (0;0 ). (1)
7.7 Determine the values of x for which g'(x) > 0 . (2)
[20]

QUESTION 8
8.1 The sum of two numbers, p and q, is 820.The greater number is p and the smaller number is q.
8.1.1 Write q in terms of p. (1)
8.1.2 Show that the product, Z, of the two numbers is given by Z = 820 p - p² . (2)
8.1.3 Determine the value of p if the product Z is a maximum. (2)
8.2 An artisan’s earning ability in rand, R, varies with the artisan’s work experience in years, x, according to the formula:
R (x) = -50x² + 3200x - 1860
8.2.1 Calculate the artisan’s earnings after 15 years’ work experience. (2)
8.2.2 Determine the maximum earnings of the artisan. (4)
[11]

QUESTION 9
9.1 Determine the integral:
9.1.1 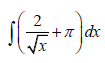 (4)
9.1.2  (4)
9.2 The sketch below shows the shaded bounded area of the curve of the function f defined by f (x) = 4x - x².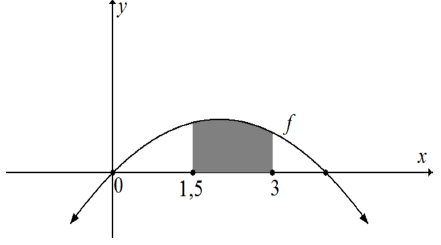

Determine (showing ALL calculations) the shaded area bounded by the curve and the x-axis between the points where x = 1, 5 and x = 3 . (6)
 [14]
TOTAAL: 150

INFORMATION SHEET: TECHNICAL MATHEMATICS P1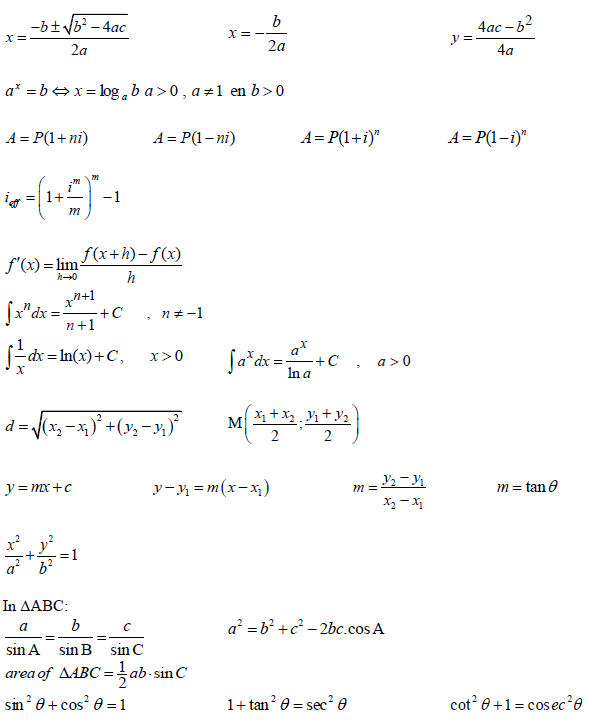

ANSWER SHEET
QUESTION 4.2.5

QUESTION 7.5