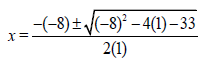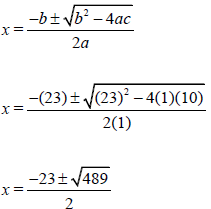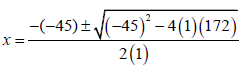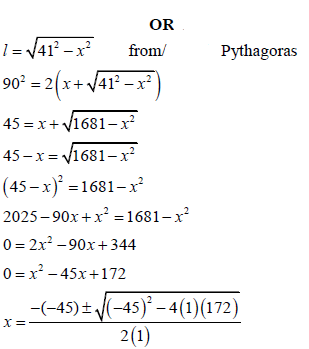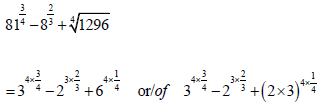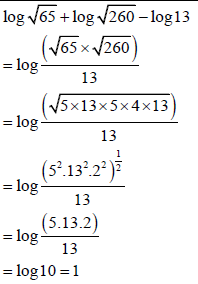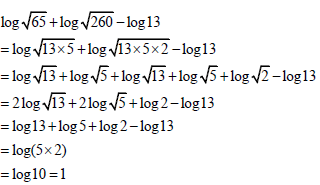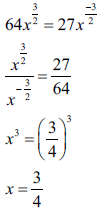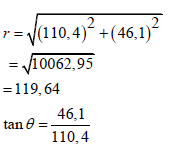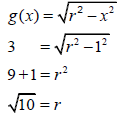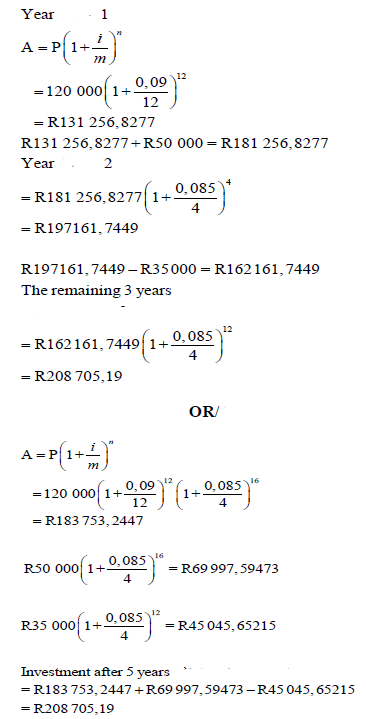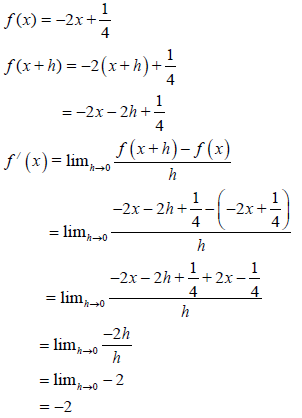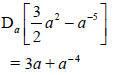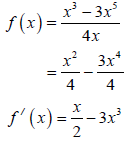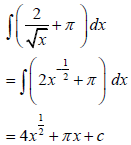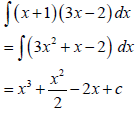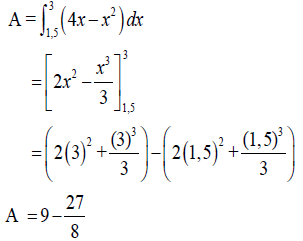Technical Mathematics Paper 1 Memorandum - Grade 12 June 2021 Exemplars

Wednesday, 23 March 2022 07:08

Technical Mathematics Paper 1 Memorandum - Grade 12 June 2021 Exemplars

More in this category: « Technical Mathematics Paper 1 Questions - Grade 12 June 2021 Exemplars Technical Mathematics Paper 2 Questions - Grade 12 June 2021 Exemplars »

Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

MARKING CODES
A	Accuracy
AO	Answer only
CA	Consistent accuracy
M	Method
R	Rounding
NPR	No penalty for rounding
NPU	No penalty for units omitted
S	Simplification
F	Correct formula
SF	Substitution in correct formula

MEMORANDUM

QUESTION 1

1.1	1.1.1	x² - 8x - 33 = 0 ( x -11)( x + 3) = 0 or ∴ x = 11 or x = -3 (8)2 2(1)  4(1)  33	🗸 Factors SF A 🗸 x = 11 🗸 x = -3 CA	(3)

	1.1.2	x² - 7x = 10 (-3x -1) x² - 7x = -30x -10 x² + 23x+10 = 0 x = - 0, 44 or x = - 22, 56	🗸S A 🗸 SF CA 🗸both values of x CA	(3)

	1.1.3	-2x² + 9x+ 5 < 0 (-2x - 1)( x - 5) < 0 C.V / K .W : - ½ and 5 Solution g : x < - ½ or x > 5	🗸 Factors SF A 🗸Critical Values CA 🗸 x< - ½ CA 🗸 x > 5 CA	(4)

1.2

P = 2(l + w)
90 = 2 (l + x)
45 - x = l
41² = x² + (45 - x)²1681 = x² + 2025 - 90x + x²0 = 2x² - 90x + 344
0 = x² - 45x + 172

x = 40, 78 or 4, 22
∴ width is 4, 22 cm

x = 40, 78 or 4, 22
∴ width is 4, 22 cm

🗸length in terms of x A

🗸M (Pyth.)       CA
🗸S       CA
🗸S       CA
🗸SF     CA
🗸width CA

🗸length in terms of x      A
🗸M (Pyth.)       CA
🗸S       CA
🗸S       CA
🗸SF     CA
🗸width / wydte            CA

(6)

1.3

x = y+ 3 and y - x² = -2x - 3
substitute x into y - x² = -2x - 3
y - ( y+ 3)² = -2(y+ 3) - 3
y - y² - 6 y - 9 = -2y - 6 - 3
- y² - 3y = 0
(- y )( y+ 3) = 0
y = 0 or y = -3
x = 0 or x = 3

🗸 Substitution A

🗸S CA

🗸 Factors SF CA

🗸 Both y-values CA

🗸 Both x-values CA

	OR x = y+ 3 and y - x² = -2x - 3 x = 3 = y and y = x² - 2x - 3 equate y: x - 3 = x² - 2x - 3 0 = x² - 3x 0 = x ( x - 3) x = 0 or x =3 y = 0 or y = -3		OR		(5)
			🗸 equating Y	A
			🗸 S	CA
			🗸 Factors	CA
			🗸 x-values	CA
			🗸 y-values	CA

1.4	1.4.1	K = 8 + 32 + 1 = 41	🗸 value of K	A	(1)

	1.4.2	41 = 1 0 1 0 0 1₂	🗸 1 0 1 0 0 1₂ From 1.4.1	CA	(1)
					[23]

QUESTION 2

2.1	Δ = b² - 4ac < 0 4 + 8m < 0 m < -½	🗸Discriminant < 0 A 🗸S CA	(2)

2.2	Δ = b² - 4ac = (-b)² - 4 (a)[-½] = 0 + 4 = 4 Roots are real, rational and unequal	🗸 SF A 🗸 S CA 🗸Real and unequal CA 🗸rational roots CA	(4)
[6]

QUESTION 3

3.1	3.1.1		🗸 Exponential form / Eksponensiële vorm 🗸 S	A CA	(2)

	3.1.2	OR	🗸Log property 🗸Exponential form 🗸S 🗸Log property OR 🗸Log property 🗸S 🗸Log property 🗸Log property	A CA CA CA A CA CA CA	(4)

3.2	-2 (log 25 - log 4) = 4 log 2 - log 5 RHS = -2 (log 5² - log 2² ) log 2 - log 5 = -2 × 2(log 5 - log 2) -(log 5 - log 2) = 4 = LHS		🗸Exponential form 🗸Log property 🗸Factors	A CA CA	(3)

3.3	3.3.1		🗸M 🗸Exponential property 🗸Exponential property	A CA CA	(3)

	3.3.2	log₃ (x - 3) - log₃ 5 = 1 log₃ ( x - 3) = log₃3 5 ( x - 3) = 3 5 x - 3 = 15 x = 18 OR log₃ (x - 3) - log₃ 5 = 1 log₃ (x - 3) = log₃ 3 + log₃ 5 log₃ ( x - 3) = log₃ (3× 5) x - 3 = 15 x = 18	🗸Log property 🗸Log property 🗸S OR 🗸Log property 🗸Log property 🗸S	A CA CA A CA CA	(3)

3.4	x - 3(5i + 2) = 4 - 3i + yi x - yi = 3(5i + 2) + 4 - 3i = 15i + 6 + 4 - 3i = 10 + 12i x = 10 y = -12 OR x - 3(5i + 2) = 4 - 3i + yi x - 15i - 6 = 4 + i (-3 + y) x - 6 - 15i = 4 + i (-3 + y) x - 6 = 4 and -15 = -3 + y x = 10 and -12 = y		🗸S 🗸x-value 🗸y-value OR 🗸S 🗸x-value 🗸y-value	A CA CA A CA CA	(3)

Related Items

3.5	V = 110, 4 + 46,1i θ = 22, 7º or θ = 180º + 22, 7º = 202, 7º z = 119, 64 cis (22, 7º) or z = 119, 64 cis 202, 7º	🗸Substitution A 🗸S CA 🗸Ratio CA 🗸 θ CA 🗸Polar form CA	(5)
[23]

QUESTION 4

4.1	4.1.1	and h(x) = ^a/_x or xy = a 3 = ^a/₁ 3×1=a ∴3 = a	🗸 SF 🗸value of r 🗸value of a	(3)

	4.1.2	0 ≤ y ≤ √10	🗸 0 and √10 CA from 4.1.2 🗸Correct notation A	(2)

	4.1.3	B(-√10;0)	🗸 Coordinates of B CA from 4.1.1	(1)

	4.1.4	y= 0 x= 0	🗸 x= 0 A 🗸 y= 0 A	(2)

4.2	4.2.1	k(x) = 2( x - 2)² - 2 k(x) = 2( x - 2)² - 2 k(0) = 2(0 - 2)² - 2 = 6 y- int. = 6 OR k(x) = 2( x - 2)² - 2 = 2(x² - 4x+ 4) - 2 = 2x² - 8x+ 6 y - intercept 6	🗸Substitution A 🗸y-int CA OR 🗸S A 🗸y-int. CA	(2)

	4.2.2	TP (2; -2)	🗸x-coordinate 🗸y-coordinate	(2)

4.2	4.2.3	k(x) = 2 ( x - 2)² - 2 = 2(x² - 4x + 4) - 2 = 2x² - 8x+ 6 x - int . ; k(x) = 0 0 = x² - 4x + 3 = ( x - 1)( x - 3) x= 1 or x= 3	🗸S A 🗸Equate to 0 CA 🗸Factors CA 🗸Both x-values CA	(4)

	4.2.4	x ∈ R	🗸 x ∈ R A	(1)

	4.2.5		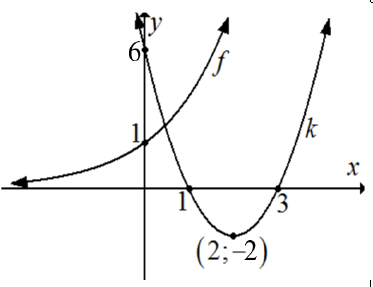f: 🗸Shape A 🗸y-intercept CA k: 🗸Shape A 🗸both x-intercepts CA 🗸y- intercept CA 🗸Turning point CA	(6)

	4.2.6	y ≥ -2	🗸 y ≥ -2 CA	(1)
[24]

QUESTION 5

5.1	A = P(1+ ni) = 35(1 + 9 × 0,15) = R82, 25	🗸SF 🗸S	A CA	(2)

5.2	A = P(1+i )ⁿ= 13 565 (1 + 0, 065)⁸= 22 450	🗸F 🗸SF 🗸S	A CA CA	(3)

5.3		🗸 SF A 🗸S CA 🗸 Sum CA 🗸 SF A 🗸S CA 🗸Difference CA 🗸SF CA 🗸S CA 🗸 SF A 🗸S CA 🗸 SF A 🗸 S CA 🗸SF A 🗸S CA 🗸S CA 🗸S CA		(8)
				[13]

QUESTION 6

6.1			🗸F A 🗸SF CA 🗸S CA 🗸S CA 🗸 f '(x) = -2 CA	(5)

6.2	6.2.1		🗸3a A 🗸a^{- 4} CA	(2)

	6.2.2		🗸S A 🗸 ^x/₂ CA 🗸 3x³ CA	(3)

	6.2.3	S = ½ ft ² ds = ft dt = πt	🗸 ft A 🗸 πt CA	(2)

6.3

6.3.3

f (x) = 3x²f'(x) = 6x
Av.grad. = f (8)- f (2)
8 - 2
= 192 - 12
8 - 2
6x = 30
x = 5

🗸6x A

🗸S CA

🗸Equating derivative and av. gradient CA

🗸 x= 5 CA

(4)

[16]

QUESTION 7

7.1	g(x) = x³ - 12x - 16 g(-2) = (-2)³ -12 (-2) -16 = 0 ∴ (x - 2) is a factor of (x)	🗸substitution by -2 A 🗸S CA	(2)

7.2	g(x) = x³ - 12x - 16 0 = ( x + 2)(x² - 2x - 8) 0 = ( x + 2)(x + 2)(x - 4) x = -2 or x = 4	🗸Equating to 0 A 🗸Quadratic factor A 🗸Factors of quadratic factor CA 🗸values of x CA	(4)

7.3	(0; -16)	🗸 y-intercept A	(1)

7.4	f(x) = x³ -12x -16 f'(x) = 3x² - 12 0 = 3x² - 12 0 = x² - 4 0 = ( x - 2)( x + 2) x = 2 or x = - 2 g (2) = (2)³ - 12(2) - 16 = -32 g (-2) = (-2)³ - (-2) -16 = 0 TP(-2; 0) and (2; -32)	🗸Derivative A 🗸0 CA 🗸Factors CA 🗸Both x values CA 🗸 (-2; 0) CA 🗸 (2; -32) CA	(6)

7.5		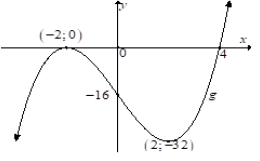🗸Shape A 🗸y-intercept CA 🗸x-intercepts CA 🗸Both turning points CA	(4)
7.6	h(x) = (x - 2)³ - 12(x - 2) -16	🗸h(x) A	(1)

7.7	-2 > x or x < 2	√ -2 > x CA 🗸 x < 2 CA	(2)
			[20]

QUESTION 8

8.1	8.1.1	q = 820 - p	🗸 q = 820 - p	A	(1)

	8.1.2	Z= pq = p (820 - p) = 820 p - p²	🗸Substitution CA 🗸S CA		(2)

	8.1.3	Z = 820 p - p²dZ = 820 - 2 p dp 0 = 820 - 2 p ∴ p= 410	🗸Derivative = 0 CA 🗸S CA		(2)

8.2	8.2.1	R ( x) = -50x² + 3200x -1860 R (15) = -50 (15)² + 3200 (15) -1860 = R34 890	🗸Substitution A 🗸S CA		(2)

	8.2.2	R (x) = -50x² + 3200x -1860 R' (x) = -100x + 3200 0 = -100x + 3200 100x= 3200 x = 32 R (x) = -50x² + 3200x - 1860 R (32) = -50 (32)² + 3200 (32) -1860 = R49340 = artisan's maximum earnings	🗸Derivative = 0 CA 🗸S CA 🗸Substitution CA 🗸S CA		(4)
					[11]

QUESTION 9

9.1	9.1.1	🗸 2x^½ A 🗸 4x^½ CA 🗸 πx A 🗸 c A	(4)
	9.1.2	🗸S A 🗸 x³ CA 🗸x² CA 2 🗸 -2x - c CA	(4)

9.2		🗸A definite integral formula A 🗸 2x² CA 🗸 -x³ CA 3 🗸Substitution in A by 3 CA 🗸Substitution in A by 1,5 CA 🗸S CA	(6)
			[14]

	TOTAL:		150

Last modified on Thursday, 31 March 2022 08:18

Published in Grade 12 June 2021 NSC Past Exam Papers and Memos