INSTRUCTIONS AND INFORMATION
Read the following instructions carefully before answering the questions.

1. This question paper consists of TEN questions.
2. Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
3. Clearly show ALL calculations, diagrams, graphs, et cetera which you have used in determining the answers.
4. Answers only will NOT necessarily be awarded full marks.
5. You may use an approved scientific calculator (non-programmable and non- graphical) unless stated otherwise.
6. If necessary, round off your answers to TWO decimal places, unless stated otherwise.
7. Diagrams are NOT necessarily drawn to scale.
8. An information sheet with formulae is included at the end of the question paper.
9. Number the answers correctly according to the numbering system used in this question paper.
10. Write neatly and legibly.

QUESTIONS

QUESTION 1
The picture below shows the inter passes amongst four soccer players in a premier league match.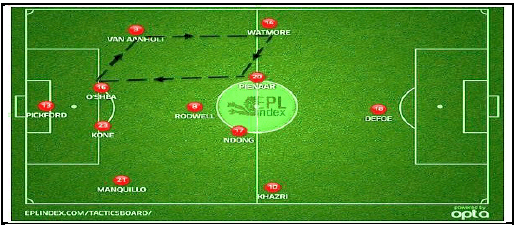

The diagram below, NOT drawn to scale, models the above situation in a Cartesian plane. The diagram below is a parallelogram with vertices A(–2 ; 2) ; B(–4 ; –1) ; C(2 ; 0) and D(4 ; 3); ? is the angle which AB forms with the x-axis.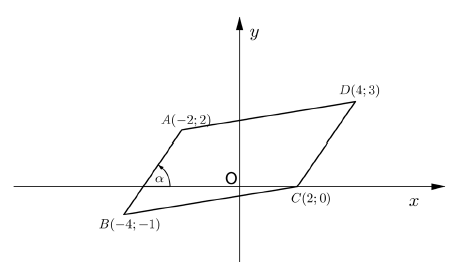

Determine:
1.1 The length of CD (Leave your answer in simplified surd form.) (2)
1.2 The equation of straight line CD in the form ? = ?? + ? (4)
1.3 The gradient of AB (1)
1.4 The size of ? (rounded off to TWO decimal places) (2)
1.5 The coordinates of M, the point of intersection of the diagonals of ABCD (2)
1.6 The equation of the straight line that is perpendicular to CD and goes through the point M. (3)
[14]

QUESTION 2
2.1 The photo below is the aerial view of a certain town. On a certain day, the community held a big function in the town hall. The noise made could be heard in a
radius of 2√2 km from the hall, centre O.

2.1.1 Calculate the equation of the circle from which the noise could be heard. (2)
2.1.2 If a car travels along the road PQ with the equation, x + y = 4 , determine the coordinates of point Q, where the passengers will be able to hear the noise from. (5)
2.1.3 After passing point Q, will the passengers be able to hear the noise? Justify your answer. (2)
2.2 The diagram below gives a schematic presentation of a cycling track. The shape of the track is given by the ellipse equation . The ellipse intersects the y-axis at B and D. N (ē; -4,8) is a point on the ellipse.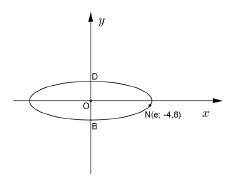

2.2.1 Write down the co-ordinates of B. (2)
2.2.2 Determine the value of e. (3)
[14]

QUESTION 3
3.1 Given: tan β = 2 ; where 90º< β < 270º.
Calculate the following with the aid of a sketch and without the use of a calculator:
3.1.1 sin β (3)
3.1.2 cot (360º - β) + 1   (2)
3.2 If θ = 72º and α = 96º, determine the following, rounded off to TWO decimal digits:
3.2.1 sin (θ + α)  (2)
3.2.2 sec α + sin ^5π/₆   (3)
3.3 If sin 24º = m , determine cos156º in terms of m. (3)
[13]

QUESTION 4
4.1 Complete the following identity: ?????²(10?) − ???²(10?) = ... (1)
4.2 Simplify the following to a single trigonometric ratio:
tan (180º - x)sin (180º + x)cos x   (7)
                  sec² x
4.3 Prove the following identity using fundamental identities and without using a sketch:
cot² x sin² x +  sin x  = 1  (3)
                      cosec x
4.4 Solve for ? ∈ [0°; 360°], rounded off to ONE decimal digit:
4.4.1 sec 2x = 2 (4)
4.4.2 2 tan (x - 30°) = -3     (5)
[20]

QUESTION 5
The diagram shows the graph of f(x) = cos 2x for x ∈[0°;360°].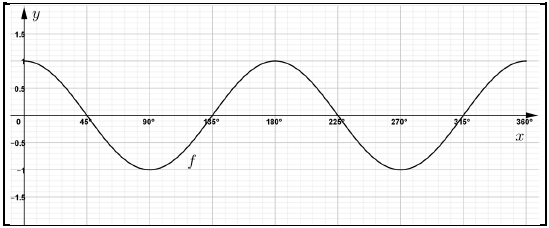

5.1 Draw, on the same set of axes in the SPECIAL ANSWER BOOK, the graph of
g(x) = sin (x - 45°) for x ∈[0°;360°].
Clearly indicate ALL the turning points, starting and end points and intercepts with the axes. (3)
5.2 Use the graphs to determine the following:
5.2.1 The amplitude of g (1)
5.2.2 The period of f (1)
5.2.3 The range of g (2)
5.2.4 f (135°) - g (135°)  (2)
5.2.5 The values of x for which f(x) = 1 for x ∈[0°;360°] (3)
5.2.6 The values of x for which f(x) < 0 for x ∈[180°;360°] (2)
5.2.7 The values of x for which f (x)g(x) ≥ 0 for x ∈[0°;360°] (2)
5.2.8 For which value(s) of x is f ́ (x) ˃ 0 for x ∈[0°;180°] (2)
[18]

QUESTION 6
6.1 Complete the following statement:
In any ∆PQR, sin P = sin Q   (1)
                         p         ...
6.2 In the diagram below, ∆ABC is drawn with D on AB. Further, BÂC = 80°, BC = 11 units, BD = 6 units and AD = 4 units.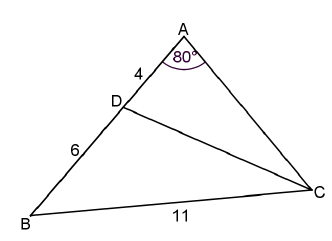

6.2.1 Calculate, rounded off to the nearest degree, the size of ABC. (4)
6.2.2 Hence or otherwise, determine the length of DC. (4)
6.2.3 Determine the area of ∆DBC. (3)
6.2.4 Determine the length of AC. (3)
[15]

QUESTION 7
7.1 Complete the following theorem:
A line drawn from the centre of a circle perpendicular to a chord … (1)
7.2 Given a circle with centre O with OR ⊥ PT, radius OB = 8 cm and PR = 2 cm.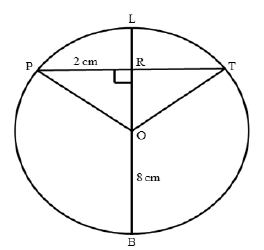

7.2.1 Determine, stating a reason, the length of PT. (3)
7.2.2 Calculate the length of LR. (4)
[8]

QUESTION 8
8.1 Complete the following theorem: Two tangents drawn to a circle from the ... outside the circle are equal in length. (1)
8.2 In the diagram below CD and DE are tangents at C and E respectively to the circle.
C, F and E lie on the circumference of the circle.
DG is parallel to FE with G on FC.
CDE = 46º and CGD = x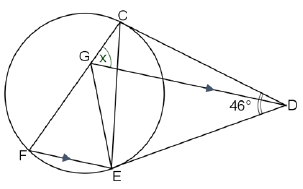

8.2.1 Determine, stating reasons, the value of x. (6)
8.2.2 Hence or otherwise show that C, G and D lie on the circumference of a circle. (2)
8.2.3 If CGED is a cyclic quadrilateral, determine, stating reasons, the size of GEF . (3)
8.2.4 Calculate the size of FGˆ E by providing at least two methods of calculating the angle. (3)
8.3 In the diagram below, BE is the diameter of the circle ABCE with centre O.
GF is a tangent to the circle at point C.
EBC = 25º and ABE = 48º .

Determine, giving reasons, the size of the following angles:
8.3.1 BÂE (2)
8.3.2 AÔE (2)
8.3.3 CÊF (2)
8.3.4 EĈF (2)
8.3.5 AĈE (2)
8.3.6 AĈG (3)
[28]

QUESTION 9
9.1 Complete the following theorem: A line drawn parallel to one side of a triangle divides the other two sides … (1)
9.2 In ΔABC below, BCisproduced to G. 

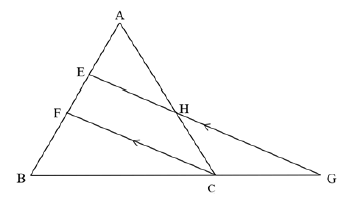
9.2.1 Complete, with reason: AE = ...  (2)
                                              EF
9.2.2 Determine the length of EF. (3)
9.2.3 If EF = 5 , determine FB.  (1)
                    2
9.2.4 Hence, or otherwise show that BG cannot be more than 3 units.  (3)
                                                          GC
[10]

QUESTION 10
In the diagram below, BCDE is a circle. Chords CB and DE are produced to meet in A.
AE = DC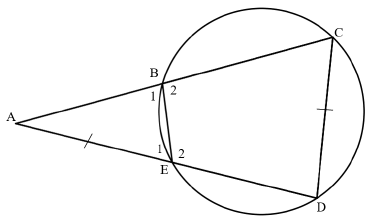

Prove that:
10.1 ΔACD ⫴ ΔAEB (4)
10.2 AC.EB = CD² (3)
10.3 Hence or otherwise, if AC = 13 cm and EB = 3 cm, calculate the length of CD. (3)
[10]

TOTAL: 150

INFORMATION SHEET