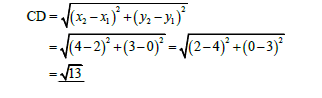ElimuZA Access to Education
Wednesday, 23 March 2022 07:09
Technical Mathematics Paper 2 Memorandum - Grade 12 June 2021 Exemplars
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupNOTE:
- Continuous accuracy (CA) applies ONLY where indicated in this marking guideline.
- Assuming values/answers in order to solve a problem is unacceptable.
MARKING CODES | |
M | Method |
A | Accuracy |
AO | Answer only |
CA | Consistent accuracy |
F | Formula |
I | Identity |
R | Rounding |
S | Simplification |
ST | Statement |
RE | Reason |
ST/RE | Statement and correct reason |
SF | Substitution into correctly the correct formula |
NPU | No penalty for omitting units |
QUESTION 1 | ||||||||
 | ||||||||
1.1 |
| √ SF | (2) | |||||
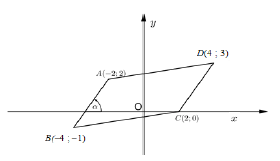
| 1.2 | mCD = y2 - y1 x2 - x1 = 3 - 0 = 0 - 3 4 - 2 2 - 4 = 3/2 Equation of CD y - y1 = m(x - x1) y - y1 = m(x - x1) y - 0 = 3/2(x - 2) OR y - 3 = 3/2(x - 4) y = 3/2x - 3 y = 3/2x - 3 | √ SF √ A √ CA gradient √ SF CA √ CA | (4) | |||||
| 1.3 | mAB = 3/2 (opp sides of II''') | √ CA | (1) | |||||
| 1.4 | tan ∝ = 3/2 ∝ = 56,31º | √ M √ CA √ CA | (2) | |||||
| 1.5 | 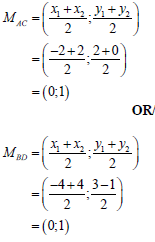 | √ SF A OR √SF A | (2) | |||||
| 1.6 | mnew line = - 1 mCD Equation of new line y - y1 = m(x - x1) y - 1 = -2/3 (x - 0) y = -2/3x + 1 | √ M CA √ SF CA √ CA | (3) | |||||
| 14 | ||||||||
| QUESTION 2 | |||
 | |||
| 2.1.1 | x2 + y2 = r2 = (2(√2)2 x2 + y2 = 8 | √ SF A √ CA | (2) |
| 2.1.2 | y = 4 - x ..... eq 1 OR x = 4 - y ..... eq 1 | √ equation1 M A OR √ equation 1 M A | (5) |
| 2.1.3 | No, 𝑂𝑄 ⊥ 𝑄𝑃 shortest distance to the centre is Q.No, 𝑂𝑄 ⊥ 𝑄𝑃 shortest distance to the centre is Q. | √ No √√ Justification | (2) |
 | |||
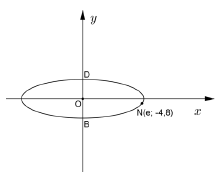| 2.2.1 | B(0;-√64) = B(0;8) | √A √A | (2) |
| 2.2.2 | 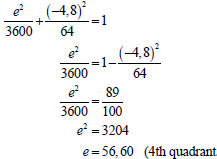 | √ SF A √ S CA √ CA | (3) |
| [14] | |||
| QUESTION 3 | |||
 | |||
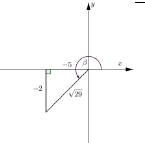| 3.1.1 | r2 = (-5)2 + (-2)2 r = √29 ∴sin β = -2 √29 | √ quadrant A √ quadran A √ value of r A √ value of ratio CA | (3) |
| 3.1.2 | cot (360º - β) + 1 = -cot β + 1 = -5/2 + 1 = -3/2 | √ -cot β I √ S CA | (2) |
| 3.2.1 | sin (θ + α) =sin (72º + 96º) = 0,21 | √ S A √ S CA AO Full marks | (2) |
| 3.2.2 | sec α + sin 5π = 1 + sin 150º 6 cos 96º = 1 + 0,5 cos 96º = -9,07 | √ 1 A cos 96º √ 0,5 √ CA AO Full marks | (3) |
| 3.3 | 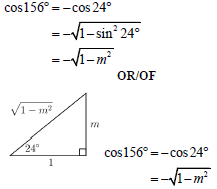 | √ -cos 24º OR √ -cos24º | (3) |
| [13] | |||
Related Items
| QUESTION 4 | |||
| 4.1 | 1 | √ S A | (1) |
| 4.2 | 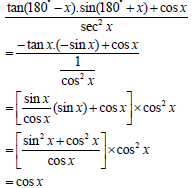 | √ -tanx I A √ -sin I A √ 1 I A cos2x √ tan x = sin x I A cos x √ S CA √ sin2x + cos2x = 1 I A √ S CA | (7) |
| 4.3 | 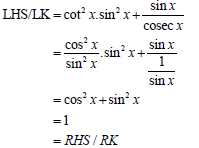 | √ cotx = cosx I A sin x √ 1 I A sin x √ sin2x + cos2x = 1 I A | (3) |
| 4.4.1 | sec 2x = 2 ∴ cos 2x = ½ Ref ∠ = 60º ∴ x - 30º = 180º - 56,3º or x - 30º = 360º - 56,3º ∴ x - 30º = 123,7º or x - 30º = 303,7º ∴ x = 153,7º or x = 333,7º | √ tan(x - 30º) = -3/2 S A √ reference √ 123,7º CA √ 303,7º CA √ 153,7º and 333,7º CA | (4) |
| 4.4.2 | (5) | ||
| [20] | |||
| QUESTION 5 | |||
 | |||
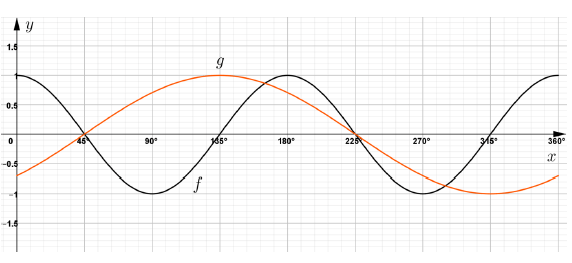| 5.1 | see diagram above | √ x-intercept A √ endpoints A √ turning points A | (3) |
| 5.2.1 | Amplitudeg = 1 | √ A | (1) |
| 5.2.2 | periodf = 360º = 180º 2 | √ A | (1) |
| 5.2.3 | rangeg : y∈ [-1;1] | √ endpoints A √ notation A | (2) |
| 5.2.4 | ƒ(135º) - g(135º) = 0 - 1 - 1 | √ function values A √ CA AO Full marks | (2) |
| 5.2.5 | x∈{0º;180º;360º} | √ A | (3) |
| 5.2.6 | x∈(225º;315º) or 225º < x < 315º | √ endpoints A √ notation A | (2) |
| 5.2.7 | x∈[135º;315º] or 135º ≤ v ≤ 315º | √ endpoints A √ notation A | (2) |
| 5.2.8 | x∈[90º;180º) or 90º < x < 180º | √ endpoints A √ notation A | (2) |
| [18] | |||
| QUESTION 6 | |||
| 6.1 | sin P = sin Q p q | √ A | (1) |
| 6.2 |  | ||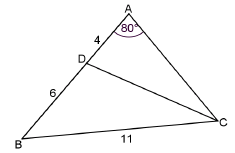
| 6.2.1 | In ΔABC: sin C = sin A c a sin C = sin 80º 10 11 sin C = 0,8952.....º C = 63,534.......º B = 180º - 80º - 63,534....º≈36 | √ SF A √ S CA √ value of c CA √ value of B R | (4) |
| 6.2.2 | In ΔDBC: DC2 = DB2 + BC2 - 2DB.BC cos B = 62 +112 - 2 × 6 × 11 cos 36º = 950,20975...... DC = 7,09cm | √ F A √ SF CA √ S CA √ CA NPU | (4) |
| 6.2.3 | Area ΔDBC = ½DB.BC sin B = ½ × 6 × 11 sin36º = 19,40cm2 | √ F A √ SF CA √ S CA NPU | (3) |
| 6.2.4 | In ΔABC: b = a sin B sin A ∴ b = 11 or sin36º sin80º ∴ b = 11sin36º sin80º ∴ b = 6,57 units In ΔABC: ∴ b = 10 sin36º sin63,53º ∴ b = 10sin36º sin63,53º ∴b = 6,57 units | √ SF CA √ S CA √ value of CA | (3) |
| [15] | |||
| QUESTION 7 | |||
| 7.1 | Bisect the chord | √ A | (1) |
| 7.2 |  | ||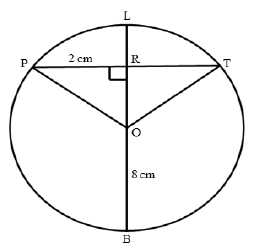
| 7.2.1 | RT = 2cm (line from centre ⊥ to chord) ∴ PT = 4 cm | √ ST √ RE √ ST NPU | (3) |
| 7.2.2 | OR2 = OP2 - PR2 (Pythagoras) = 82 - 22 = 60 OR = 2√15 LR = 8 - 2√15 ∴ LR = 0,25 units | √ M Pythagoras √ ST A √ length of OR S CA √ length of LR S CA NPU | (4) |
| [8] | |||
| QUESTION 8 | |||
| 8.1 | Same point | √ A | (1) |
 | |||
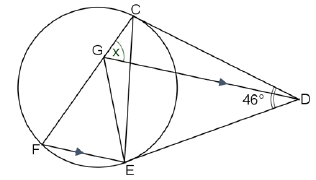| 8.2.1 | DCE = DEC (tangents from common point) DCE = DEC =180º - 46º (∠s of Δ and ∠s opp = sides) 2 = 67º F = 67º (tan-chord) CGD = x = 67º | √ ST √RE √ ST RE √ ST √RE √ ST RE | (6) |
| 8.2.2 | From 8.2.1 DCE = DGC ∴ CGD is a circle (converse tan-chord th) | √ ST √ RE | (2) |
| 8.2.3 | EGD = ECD (∠s in same segment) ∴ EGD = 67º ∴ GEF = 67º (alt ∠ s; GD II FE) | √ ST √ RE √ ST RE | (3) |
| 8.2.4 | FGE = 46º [Int ∠s of Δ or ∠s on str lineor ext ∠ of cyclic quad] | √ ST √ RE √ RE (Any two) | (3) |
| 8.3 |  | ||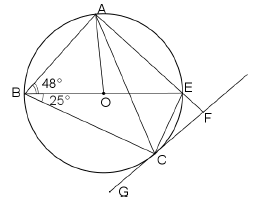
| 8.3.1 | BAE = 90º (∠ in semi-circlce) | √ ST √ RE | (2) |
| 8.3.2 | AOE = 96º (∠ at center = 2 × ∠ at circumf) | √ ST √ RE | (2) |
| 8.3.3 | CEF = 73º (ext ∠ of cyclic quad) | √ ST √ RE | (2) |
| 8.3.4 | ECF = 25º (tan-chord) | √ ST √ RE | (2) |
| 8.3.5 | ACE = 48º (∠s in the same segm) | √ ST √ RE | (2) |
| 8.3.6 | AEC = 107º (∠s on straight line OR opp ∠s of cyclic quad) ACG = 107º (tan-chord) | √ ST √ RE √ ST RE | (3) |
| [28] | ||
| QUESTION 9 | |||
| 9.1 | proportionally | √ A | (1) |
 | |||
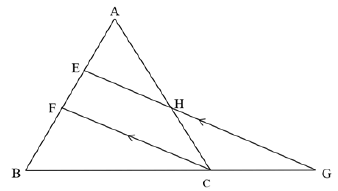| 9.2.1 | AE = AH (line III one side of Δ OR prop th; EH II FC) EF HC | √ ST √ RE | (2) |
| 9.2.2 | AE = AH (from 9.2.1) EF HC 3 = 6 EF 5 EF = 15 6 = 5 2 | √ ST √ CA √ ST √ CA √ ST √ CA | (3) |
| 9.2.3 | BF = 7 - EF = 7 - 5 2 = 9 2 | √ ST √ CA | (1) |
| 9.2.4 | In ΔBEG: BC = BF (line II one side of Δ OR prop th; EH III FC) CG FE = 4,5 2,5 = 1,8 < 3 | √ ST √ RE √ ST √ conclusion | (3) |
| [10] | |||
| QUESTION 10 | |||
 | |||
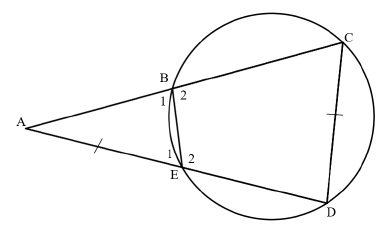| 10.1 | In ΔACD and ΔAEB: 1) A is common 2) C = E1 ( ext ∠ of cyclic quad) 3) D = B1 (Int ∠s of Δ or ext ∠ of cyclic quad) ∴ ΔACD III ΔAEB (AAA) | √ ST √ RE √ ST √ mark is either for 3rd angle or for the reason AAA | (3) |
| 10.2 | AC = CD (ΔACD /// ΔAEB) AE EB ∴ AC = CD (AE = DC; given) CD EB ∴ CD2 = AC.EB | √ ST √ RE √ ST A | (3) |
| 10.3 | CD2 = 13 × 3 CD = √39 ≈ 6,24 cm | √ ST A √ M A √ Value of CD CA | (3) |
| [10] | |||
| Total: | 150 | ||
Published in Grade 12 June 2021 NSC Past Exam Papers and Memos