PHYSICAL SCIENCES PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2021

More in this category: « PHYSICAL SCIENCES PAPER 1 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2021 PHYSICAL SCIENCES PAPER 2 GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2021 »

Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

QUESTION 1
1.1 A ✓✓ (2)
1.2 B ✓✓ (2)
1.3 D ✓✓ (2)
1.4 B ✓✓ (2)
1.5 C ✓✓ (2)
1.6 D ✓✓ (2)
1.7 B or/✓✓ (2)
1.8 A or V1✓✓ (2)
1.9 D ✓✓ (2)
1.10 D ✓✓ (2)
[20]

QUESTION 2
2.1

Marking criteria

If any of the underlined key words/phrases in the correct context is omitted deduct 1 mark

A body will remain in its state of rest or motion at constant velocity unless a non-zero resultant/net force/unbalanced force acts on it. ✓✓

OR
A body will remain in its state of rest or uniform motion in a straight line unless a (non-zero) resultant/net /unbalanced force acts on it. ✓✓ (2)

2.2

Accepted labels
w	F_g / F_w / weight / mg /196 N / gravitational force
F	F_A / Applied force
fk	(kinetic) Friction / F_f / f /18 N / F_w / f_w
N	F_N / Normal / 169,74 N

Notes

Mark awarded for label and arrow, but penalise only once if arrows are omitted
Do not penalise for length of arrows, drawing is not to scale..
Any other additional force(s) deduct 1 mark.
If force(s) do not make contact with body deduct 1 mark.

(4)

2.3

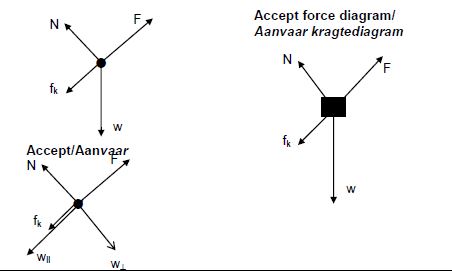
OPTION 1
Positive up the incline
F_net = ma
F+ f_k + w_ll = ma
F+ (-f_k) + (-w_ll) = ma
F - (f_k + w_ll) = ma
F - [18 + (20)(9,8)(sin30º)] ✓ = 0 ✓
F = 116 N ✓

NOTE
F_net = 0
F = f_k + w_II

OPTION 2
Positive up the incline
W_net = ΔEk ✓
FΔxcos0º + fΔxcos180º + wΔxcos120º ✓= 0 ✓
FΔx = 18Δx + (20)(9,8)Δx(0,5)
F = 116 N ✓

NOTE
Wnet = 0
FΔx = fΔx + wΔx(0,5)

(4)

2.4 POSITIVE MARKING FROM QUESTION 2.3

116 N / f + w_|| ✓Down the incline/opposite to direction of motion helling af

ACCEPT
Downwards/down (2)

2.5 POSITIVE MARKING FROM QUESTION 2.4

OPTION 1

Up the incline positive
F_net = ma
-116 = 20a ✓
a = -5,80 m∙s^-2

vf² = vi² + 2aΔx ✓
0 =(2)² + (2)(-5,8)Δx✓
Δx = 0,34 m ✓

v_f = v_i +Δt
0 = 2 + (-5,8)Δt
Δt = 0,34 s

OR
F_netΔt = m(v_f – v_i)
(-116)Δt = (20)(0 – 2)
Δt = 0,34 s
Δx = v_iΔt + ½ aΔt² ✓
=(2)(0,34) + ½(-5,8) (0,34)²✓
= 0,34 m ✓

v_f = v_i +Δt
0 = 2 + (-5,8)Δt
Δt = 0,34 s

OR
F_netΔt = m(v_f – v_i)
(-116)Δt = (20)(0–2)
Δt= 0,34 s

Δx = (vi + vf) Δt
2
= (2 + 0)0,34
2
= 0,34 m ✓

OPTION 1

Down the incline positive
F_net = ma
116 = 20a ✓
a = 5,80 m∙s^-2

vf² = vi² + 2aΔx ✓
0 =(-2)² + (2)(5,8)Δx✓
Δx = -0,34 m
Distance = 0,34 m ✓

v_f = v_i + aΔt
0 = -2 + (5,8)Δt
Δt = 0,34 s
OR
F_netΔt = m(vf – vi)
(116)Δt = (20)(0 – (-2))
Δt = 0,34 s

Δx = viΔt + ½ aΔt2 ✓
= (-2)(0,34) + ½(5,8)(0,34)²✓
= -0,34 m ✓
Distance = 0,34 m ✓

v_f = v_i + aΔt
0 = -2 + (5,8)Δt
Δt = 0,34 s

OR
FnetΔt = m(v_f – v_i)
(116)Δt =(20)(0-(-2))
Δt = 0,34 s

Δx = (v1 + vf)Δt
2
= (-2 + 0)= -0,34 m ✓
2
= -0.34
Distance = 0,34 m ✓

OPTION 2

W_net = ΔE_K
F_netΔxcosθ = ½m(vf² - vi²)
(116)Δxcos180º ✓= ½(20)(0² – 2²) ✓
Δx = 0,34 m ✓

OPTION 3

W_net = ΔEK
W_f + W_wll= ½mvf² - ½mvi²
fΔxcosθ + (mgsin30º)Δxcosθ = ½m(vf² - vi²)
(18)Δxcos180º + (20)(9,8)sin30ºΔxcos180º✓= ½(20)(0² – 2²) ✓
Δx = 0,34 m ✓

OPTION 4

W_net = ΔEK
W_f + W_w = ½mvf² - ½mvi²
fΔxcosθ + mgΔxcos120° = ½m(vf² - vi²)
(18)Δxcos180º + (20)(9,8)Δxcos120º✓= ½(20)(0² – 2²) ✓
Δx = 0,34 m ✓

OPTION 5

W_nc = ΔE_p + ΔE_k
fΔxcosθ = mg(h_f - h_i) + ½m(vf² – vi²)
18Δxcos180º✓ = 20(9,8)Δx + ½(20)(0² – 2²) ✓
-18Δx = 196Δxsin30º - 40
Δx = 0,34 m ✓

(4)
[16]

QUESTION 3
3.1 No

ANY ONE

Gravitational force is not the only force acting on the balloon. /There are other forces acting on the balloon. ✓
Its acceleration is not 9,8 m∙s-2/is zero.
It has constant velocity/no acceleration. (2)

3.2.1

OPTION 1
UPWARDS AS POSITIVE
v_f² = v_i² + 2aΔy ✓
(-62,68)² = vi² + 2(-9,8)(-200) ✓
vi = 2,96 m∙s^-1 ✓

DOWNWARDS AS POSITIVE
vf² = vi² + 2aΔy ✓
(62,68)² = vi² + 2(9,8)(200) ✓
vi = -2,96 m∙s^-1
= 2,96 m∙s^-1 ✓

OPTION 2

(E_mech/meg)200 m = (E_mech/meg)_bottom
(E_P +E_K)_{200 m} = (E_P +E_K)_bottom
(mgh + ½ mv²)200 m = (mgh + ½ mv²)_bottom
m(9,8)(200) + ½m(v²) = 0 + ½m(62,68)² ✓
vi = 2,96 m∙s^-1 ✓

NOTE
Mass may be omitted during substitution.

OPTION 3

W_nc = ΔE_p + ΔE_k
0 = mg(h_f - h_i)+ ½m(vf² – vi²)
0 = m(9,8)(0 - 200) + ½m(62,68² – vi²) ✓
v_i = 2,96 m∙s^-1 ✓

NOTE
Mass may be omitted during substitution.

OPTION 4

W_net = ΔE_k
FnetΔxcos θ = ½m(vf² – vi²)
mgΔxcos θ = ½m(vf² – vi²)
m(9,8)(200) = + ½m(62,68² – v_i²) ✓
v_i = 2,96 m∙s-1 ✓

NOTE
Mass may be omitted during substitution.

(3)

3.2.2 POSITIVE MARKING FROM QUESTION

Marking criteria Formula to calculate Δt of stone A ✓ Substitution to calculate Δt of stone A ✓ Final answer6,70 s ✓ Accept (6,69 to/tot 6,7)
NOTE: The calculation of Δt for A might be split up into two parts.
OPTION 1 UPWARDS AS POSITIVE v_f = v_i + aΔt ✓ -62,68 = 2,96 + (-9,8)Δt ✓ Δt = 6,70 s ✓ (6,698)	DOWNWARDS AS POSITIVE v_f = v_i + aΔt ✓ 62,68 = -2,96 + 9,8Δt ✓ Δt = 6,70 s ✓ (6,698)
OPTION 2 UPWARDS AS POSITIVE Δy = v_iΔt + ½ aΔt² ✓ -200 = (2,96)Δt + ½ (-9,8)Δt²✓ Δt = 6,70 s ✓ (6,697)	DOWNWARDS AS POSITIVE Δy = viΔt + ½ aΔt² ✓ 200 = (-2,96) Δt + ½ (9,8)Δt² ✓ Δt = 6,70 s ✓ (6,697)
OPTION 3 UPWARDS AS POSITIVE Δy= (vi + vf)Δt 2 -200 = (+296 + (-62.68)) Δt 2 Δt = 6,70 s ✓ (6,698)	DOWNWARDS AS POSITIVE Δy = (vi + vf)Δt 2 200 = (- 2,96 + 62,68) Δt✓ 2 Δt = 6,70 s ✓ (6,698)
OPTION 4 UPWARDS AS POSITIVE From 200 m upwards: v_f = v_i + aΔt ✓ 0 = 2,96 + (-9,8)Δt ✓ Δt = 0,3 s (0,302) From max h downwards: v_f = v_i + aΔt -62,68 = 0 + (-9,8)Δt Δt = 6,40 s (6,369) t_A = 0,3 + 6,40 = 6,7 s ✓	DOWNWARDS AS POSITIVE From 200 m upwards: v = v_i + aΔt ✓ 0 = -2,96 + (9,8)Δt ✓ Δt = 0,3 s (0,302) From max h downwards: v_f = v_i + aΔt 62,68 = 0 + (9,8)Δt Δt = 6,40 s (6,369) t_A = 0,3 + 6,40 = 6,7 s ✓
OPTION 5 UPWARDS AS POSITIVE From 200 m upwards: vf = vi + aΔt ✓ 0 = 2,96 + (-9,8)Δt ✓ Δt = 0,3 s (0,302) From 200 m downwards: vf = vi + aΔt -62,68 = -2,96 + (-9,8)Δt Δt = 6,09 s (6,094) tA = 2(0,3) + 6,09 = 6,69 s ✓	DOWNWARDS AS POSITIVE From 200 m upwards: vf = vi + aΔt ✓ 0 = -2,96 + (9,8)Δt ✓ Δt = 0,3 s (0,302) From 200 m downwards: vf = vi + aΔt 62,68 = 2,96 + (9,8)Δt Δt = 6,09 s (6,094) tA = 2(0,3) + 6,09 = 6,69 s ✓
OPTION 6 UPWARDS AS POSITIVE FnetΔt = m(vf – vi) ✓ mgΔt = m(vf – vi) gΔt = vf - vi (-9,8)Δt = (-62,68) – (2,96) ✓ Δt = 6,69 s ✓	DOWNWARDS AS POSITIVE FnetΔt = m(vf – vi) ✓ mgΔt = m(vf – vi) gΔt = vf - vi (9,8)Δt = 62,68 – (-2,96) ✓ Δt = 6,69 s ✓ (3)

3.2.3 POSITIVE MARKING FROM QUESTION 3.2.1 and QUESTION 3.2.2

Marking criteria

Formula to calculate Δy of stone B ✓
Substitution of t = 1,7 s ✓ (tA – 5)
Substitution to calculate Δy of stone B ✓
Substitution to calculate Δy of balloon ✓
Calculating distance between balloon and stone B ✓
Final answer (14,11 to/tot 14,16)

OPTION 1
UPWARDS AS POSITIVE

Stone B
Δy = v_iΔt + ½ aΔt² ✓
= 2,96(6,7 - 5)+ ½(-9,8)(6,7- 5)² ✓
= -9,13 m (-9,09 to/tot -9,13)
Distance travelled by stone B: 9,13 m

Hot-air balloon
Δy = v_iΔt + ½ aΔt²
= 2,96(6,7 - 5) ✓ + 0
= 5,03 m
Distance travelled by hot-air balloon5,03 m
Distance between hot-air balloon and stone
B = 9,13 + 5,03 ✓
= 14,16 m ✓ (14,11 - 14,16)

DOWNWARDS AS POSITIVE

Stone B
Δy = v_iΔt + ½ aΔt²✓
= -2,96(6,7 - 5) + ½(9,8)(6,7 - 5)² ✓
= 9,13 m (9,09 to/tot 9,13)
Distance travelled by stone B: 9,13 m

Hot-air balloon
Δy = v_iΔt + ½ aΔt²
= -2,96(6,7 - 5) ✓ + 0
= -5,03 m
Distance travelled by hot-air balloon 5,03 m
Distance between hot-air balloon and stone
B= 9,13 + 5,03 ✓
= 14,16 m ✓ (14,11 - 14,16)

OPTION 2
UPWARDS AS POSITIVE

Stone B
v_f = v_i + aΔt
= 2,96 + (-9,8)(6,70 – 5)
= - 13,7 m∙s^-1
vf² = vi² + 2aΔy ✓
(-13,7)² = (2,96)² + 2(-9,8)Δy ✓
Δy = -9,13 m
Distance travelled by stone B: 9,13 m

Hot-air balloon
Δy = viΔt + ½ aΔt²
= -2,96(6,70 - 5) + 0 ✓
= -5,03 m
Distance travelled by hot-air balloon/
5,03 m
Distance between hot-air balloon and

= 9,13+ 5,03 ✓
= 14,16 m ✓ (14,11 - 14,16)

DOWNWARDS AS POSITIVE

Stone B
v_f = v_i + aΔt
= -2,96 + (9,8)(6,70 – 5)
= 13,7 m∙s^-1
vf² = vi² + 2aΔy ✓
(13,7)² = (-2,96)2 + 2(9,8)Δy ✓
Δy = 9,13 m
Distance travelled by stone B: 9,13 m

Hot-air balloon
Δy = v_iΔt + ½ aΔt²
= -2,96(6,70 - 5) + 0 ✓
= -5,03 m
Distance travelled by hot-air balloon/

Distance between hot-air balloon and

= 9,13+ 5,03 ✓
= 14,16 m ✓ (14,11 - 14,16)

OPTION 3
UPWARDS AS POSITIVE

Stone B
v_f = v_i + aΔt
= 2,96 + (-9,8)(6,70 – 5)
= - 13,7 m∙s^-1
Δy = (vi + vf)Δt
2
= (+ 2,96 ( 13,7) (6,70 – 5)
2
= -9,13 m
Distance travelled by stone B: 9,13 m

Hot-air balloon
Δy = viΔt + ½ aΔt²
= 2,96(6,70 - 5) + 0 ✓
= 5,03 m
Distance travelled by hot-air balloon/
5,03 m
Distance between hot-air balloon and
stone B
= 9,13 + 5,03 ✓
= 14,16 m ✓ (14,11 - 14,16)

DOWNWARDS AS POSITIVE

Stone B
v_f = v_i + aΔt
= -2,96 + (9,8)(6,70 – 5)
= 13,7 m∙s^-1
Δy = (vI + vf)Δt
2
= (-2,96 + (13,7)) (6,70 – 5)
2
= 9,13 m
Distance travelled by stone B: 9,13 m

Hot-air balloon

Δy = vI Δt + ½ aΔt²
= -2,96(6,70 - 5) + 0 ✓
= -5,03 m
Distance travelled by hot-air balloon/ : 5,03 m
Distance between hot-air balloon and
stone B= 9,13+ 5,03 ✓
= 14,16 m ✓ (14,11 - 14,16)

OPTION 4
UPWARDS POSITIVE

Stone B
v_f = v_i + aΔt
= 2,96 + (-9,8)(6,70 – 5)
= - 13,7 m∙s^-1
Balloon's height after 5 s: 214,8 m

E_mech)214,8 m = (E_mech)1,7 s
(E_P +E_K)_{214,8 m} = (E_P +E_K)1,7 s ✓
(mgh+½ mv²) = (mgh+½ mv²)1,7s
(9,8)(214,9)+½(2,96)² =
(9,8)h+½(13,7)²
∴h = 205,67 m
Distance travelled by stone B/
214,8 – 205,67 = 9,13 m

Hot-air balloon
Δy = v_IΔt + ½aΔt²
= 2,96(6,70 - 5) ✓ + 0
= 5,03 m
Distance travelled by hot-air balloon/
5,03 m
Distance between hot-air balloon and
stone B
B: 9,13 + 5,03 ✓ = 14,16 m ✓
(14,11 to 14,16)

DOWNWARDS POSITIVE

Stone B
v_f = v_i + aΔt
= -2,96 + (9,8)(6,70 – 5)
= 13,7 m∙s^-13
Balloon's height after 5 s: 214,8 m

(E_mech)214,8 m = (E_mech)1,7 s
(E_P +E_K)214,8 m = (E_P +E_K)1,7 s ✓
(mgh +½ mv²) = (mgh + ½ mv²)1,7s
(9,8)(214,8)+½(2,96)² =
(9,8)h+½(13,7)²
∴h = 205,67 m
Distance travelled by stone B/

214,8 – 205,67 = 9,13 m
Hot-air balloon
Δy = v_IΔt + ½aΔt²
= -2,96(6,70 - 5) ✓ + 0
= -5,03 m
Distance travelled by hot-air balloon/
5,03 m
Distance between hot-air balloon and
stone B9,13 + 5,03 ✓ = 14,16 m ✓
(14,11 to/tot 14,16)

OPTION 5
UPWARDS AS POSITIVE

Stone B
v_f = v_i + aΔt
= 2,96 + (-9,8)(6,70 – 5)
= - 13,7 m∙s^-1
W_net = ΔEK ✓
F_netΔxcosθ = ½mvf2 - ½mvi²= ½m(v_f²- v_i²)
(9,8)Δhcos 0° = ½(13,72 – 2,962) ✓
Δh = 9,13 m
Distance travelled by stone B/
9,13 m
Hot-air balloon
Δy = v_IΔt + ½aΔt²
= 2,96(6,70 - 5) ✓ + 0
= 5,03 m
Distance travelled by hot-air balloon/
5,03 m
Distance between hot-air balloon and
stone B/9,13 + 5,03 ✓ = 14,16 m ✓
(14,11 to/tot 14,16)

DOWNWARDS AS POSITIVE

Stone B
v_f = v_i + aΔt
= -2,96 + (9,8)(6,70 – 5)
= 13,7 m∙s^-1
W_net = ΔEK ✓
F_netΔxcosθ = ½mv_f² - ½mv_i²= ½m(v_f^2- v_i²)
(9,8)Δhcos0° = ½(13,72 – 2,962) ✓
Δh = 9,13 m
Distance travelled by stone B/
9,13 m
Hot-air balloon
Δy = v_IΔt + ½aΔt²
= -2,96(6,70 - 5) ✓ + 0
= -5,03 m
Distance travelled by hot-air balloon/
5,03 m
Distance between hot-air balloon and
stone B 9,13+ 5,03 ✓ = 14,16 m ✓
(14,11 to/tot 14,16)

OPTION 6
Using relative velocities

UPWARDS AS POSITIVE

Δy = v_IΔt + ½aΔt²
= (2,96 - 2,96)(1,7) + ½(-9,8)(1,7)²
= -14,16 m
Distance between hot-air balloon and
stone B 14, 16m

DOWNWARDS AS POSITIVE

Δy = v_IΔt + ½aΔt²
= (2,96 - 2,96)(1,7) + ½ (9,8)(1,7)2
= 14,16 m ✓

OPTION 7
UPWARDS AS POSITIVE

Δy = v_IΔt + ½aΔt²
= (2,96)(1,7) + ½ (-9,8)(1,7)2 ✓
= -9,13 m

Distance travelled by stone B: 9,13 m
Δy = viΔt + ½ aΔt²✓
= (-2,96)(1,7) + ½(9,8)(1,7)2 ✓
= 9,13 m
Height of stone B from the ground = 200 + 14,8 – 9,13 = 205,63 m
Height of balloon from the ground = 200 + (6,7)(2,96)✓ = 219,83 m
Distance between B and the balloon = 219,83 – 205,63 ✓ = 14,16 m✓

(6)
3.3

Criteria for graph
Correct shape for stone A not starting from 0 m.	✓
Correct shape and initial position for hot-air balloon.	✓
Gradient for hot-air balloon is higher than that of stone A until stone A reaches the maximum height	✓
Both graphs starting at the same position and ending at the same time.	✓

(4)
[18]

QUESTION 4
4.1

Marking criteria
If any of the underlined key words/phrases in the correct context is omitted deduct
1 mark.
NOTE/
If “total” is omitted: minus 1 mark

A collision in which both the total momentum and total kinetic energy are conserved.✓✓
(2)
4.2

OPTION 1

ΣE_Ki = ΣE_Kf
½m₁v²_1i + ½m₂v²_i2 = ½m₁v²_f1 + ½m₂v²_f2
½mxv²ix + ½myv 2 iy = ½mxv 2fx+ ½myv 2fy
½(10)(2)² + ½(2)v²_iy ✓ = 0 + 36 ✓
v_y = ± 4 m∙s^-1
v_y = 4 m∙s^-1 west✓ACCEPT/ left

OPTION 2

E_Ki = ½ m_Yv_f²
36 = ½ (2) v_f²
vf = 6 m∙s^-1

Σp_i = Σp_f
m₁v_1i + m₂v_2i = m₁v_1f + m₂v_2f
m_xv_xi + m_yv_yi = m_Xv_xf + m_yv_yf
(10)(2) + (2)v_y ✓ = 0 + (2)(6)✓
vy = -4 m∙s^-1
vy = 4 m∙s^-1 ✓ west✓ ACCEPTleft/links

OPTION 3

E_Ki = ½ m_Yv_f²
36 = ½ (2) v_f²
vf = 6 m∙s^-1

Δp_X = -Δp_Y
mx(v_Xf - v_Xi) = - mY(v_Yf – v_Yi)
(10)(0 – 2)✓ = -(2)(6 – v_Y) ✓
vY_f = -4 m∙s^-1
vy = 4 m∙s^-1 ✓west/wes✓ ACCEPT left
(5)

4.3 POSITIVE MARKING FROM QUESTION 4.2 FOR Y; OPTIONS 1, 3 and 6

OPTION 1 EAST POSITIVE: For Y/Vir Y: F_netΔt = Δp F_netΔt = m(v_f – v_i) F_net (0,1) = 2{6 - (-4)} ✓ F_net = 200 N ✓	WEST POSITIVE For Y/Vir Y: F_netΔt = Δp F_netΔt = m(v_f – v_i) F_net (0,1) = 2(-6 - 4) ✓ F_net = -200 N F_net = 200 N ✓
OPTION 2 EAST POSITIVE: For X/Vir X: F_netΔt = Δp F_netΔt = m(v_f – v_i) F_net (0,1) = 10(0 - 2) ✓ F_net = -200 N F_net = 200 N ✓	WEST POSITIVE For X/Vir X: F_netΔt = Δp F_netΔt = m(v_f – v_i) F_net (0,1) = 10{0 - (-2)} ✓ F_net = 200 N ✓
OPTION 3 EAST POSITIVE: For Y/Vir Y: v_f = v_i + aΔt 6 = -4 + a(0,1) a = 100 m∙s^-2 F_net = ma ✓ = 2(100) ✓ = 200 N ✓	WEST POSITIVE For Y/Vir Y: v_f = v_i + aΔt -6 = 4 + a(0,1) a = -100 m∙s^-2 F_net = ma ✓ = 2(-100) ✓ = -200 N F_net = 200 N ✓
OPTION 4/OPSIE 4 EAST POSITIVE: For X/Vir X: v_f = v_i + aΔt 0 = 2 + a(0,1) a = -20 m∙s^-2 F_net = ma ✓ = 10(-20) ✓ = -200 N F_net = 200 N ✓	WEST POSITIVE For X/Vir X: v_f = v_i + aΔt 0 = -2 + a(0,1) a = 20 m∙s^-2 F_net = ma ✓ = 10(20) ✓ F_net = 200 N ✓
OPTION 5 EAST POSITIVE For X/Vir X: vf = vi + aΔt 0 = 2 + a(0,1) a = -20 m∙s^-2 vf² = vi² + 2aΔx 0 = (2)² + 2(-20)Δx Δx = 0,10 m Δx = (vf + vI)Δt 2 (0 + 2)(0,1) 2 = 0,10 m Wnet = ΔEk ✓ F_netΔxcosθ = ½ m(v_f² – v_i²) Fnet(0,1)cos180º = ½ (10)(0² – 2²) ✓ Fnet = 200 N ✓
OPTION 5 WEST POSITIVE For X/Vir X: vf = vi + aΔt 0 = -2 + a(0,1) a = -20 m∙s^-2 vf² = vi² + 2aΔx 0 = (-2)² + 2(-20)Δx Δx = 0,10 m Δx = (vf + vI)Δt 2 (0 + (-2))(0,1) 2 = 0,10 m Wnet = ΔEk ✓ F_netΔxcosθ = ½ m(v_f² – v_i²) Fnet(0,1)cos180º = ½ (10)(0² – 2²) ✓ Fnet = 200 N ✓
OPTION 6/OPSIE 6 EAST POSITIVE/OOS POSITIEF: For X/Vir X: vf = vi + aΔt 6 = -4 + a(0,1) a = 100 m∙s^-2 vf² = vi² + 2aΔx (6)² = (-4)² + 2(100)Δx Δx = 0,10 m Δx = (vf + vI)Δt 2 (6 - 4 )(0,1) 2 = 0,10 m Wnet = ΔEk ✓ F_netΔxcosθ = ½ m(v_f² – v_i²) Fnet(0,1)cos180º = ½ (2)(6² – (-4)²) ✓ Fnet = 200 N ✓
OPTION 6/OPSIE 6 WEST POSITIVE/WES POSITIEF: For X/Vir X: vf = vi + aΔt -6 = 4 + a(0,1) a = -100 m∙s^-2 vf² = vi² + 2aΔx (-6)² = (-4)² + 2(-100)Δx Δx = 0,10 m Δx = (vf + vI)Δt 2 (-6 + 4)(0,1) 2 = 0,10 m Wnet = ΔEk ✓ F_netΔxcosθ = ½ m(v_f² – v_i²) Fnet(0,1)cos180º = ½ (2)((-6)² – (4)²) ✓ Fnet = 200 N ✓

(3)
[10]

QUESTION 5

5.1

Marking criteria
If any of the underlined key words/phrases in the correct context is omitted deduct
1 mark.
ACCEPT
For isolated system:
Closed system
Only conservative forces act on the system/
No external forces act on system

The total mechanical energy in an isolated system remains constant / thesame. ✓✓

OR
The sum of the kinetic and gravitational potential energies in an isolated
system remains constant/the same.

(2)
5.2

NOTE

Mass may be omitted during substitution.
If equations of motion are used. Max 1/3 for correct answer

OPTION 1

E_{P/mech top} = E _{Q/mech ground}
(E_p + E_k)_P/top = (E_p + E_k)Q_/bottom
(mgh + ½mv²)P/top = (mgh + ½mv2)_Q/bottom
(2)(9,8)(5) + 0 = 0 + ½(2)v ²_f ✓
v_f = 9,90 m∙s^-1 ✓ (9,899)

OPTION 2

ΔE_p + ΔE_K = 0
(mgh_f - mgh_i) + ½m(v_f² – v_i²) = 0
0 - (2)(9,8)(5) + ½(2)(v_f² – 0) ✓ = 0
v_f = 9,90 m∙s^-1 ✓ (9,899)

(3)
5.3 POSITIVE MARKING FROM QUESTION 5.2.

OPTION 1

Wnet = ΔEK
Wf = ½mv_f² - ½mv_i²
W_N + W_f + W_w= ½mv_f² - ½mv_i²
fΔxcosθ = ½m(vf²- vi²)
f(10)cos180° ✓= ½(2)(4² – 9,90²) ✓
f = 8,2 N ✓

OPTION 2

Wnc = ΔEK + ΔEp
Wf = ½mv_f² - ½mv_i²
W_N + W_f = ½mv_f² - ½mv_i²
fΔxcosθ = ½m(v_f² – v_i²) + mg(h_f – h_i)
f(10)cos180° ✓= ½(2)(4² – 9,90²) + 0 ✓
f = 8,2 N ✓
(4)

5.4

LEFT NEGATIVE

FnetΔt = Δp
FnetΔt = mvf - mvi
FnetΔt = m(vf - vi)
-14 = 2(v_f – 4) ✓
v_f = -3 m∙s^-1

ΔE_K = ½mv_f² - ½mv_i² ✓
= ½(2)[(-3)2 - 42] ✓
= -7 J ✓
ACCEPT
Impulse= mΔv
Do not penalise if +3 is substituted.

ACCEPT
ΔE_K = ½mv_f² - ½mv_i² ✓
= ½(2)[(0)² – (-3)²] ✓
= -9 J ✓
Do not penalise if +3 is substituted.

RIGHT NEGATIVE
FnetΔt = Δp
FnetΔt = mv_f - mv_i
FnetΔt = m(v_f - v_i)
14 = 2(v_f – (-4)) ✓
vf = 3 m∙s^-1

ΔEK = ½mv_f² - ½mv_i² ✓
= ½(2)[(3)² – (-4)²] ✓= -7 J ✓
ACCEPT
Impulse = mΔv
Do not penalise if +4 is substituted.

ACCEPT
ΔEK = ½mv_f² - ½mv_i² ✓
= ½(2)[(0)²– (-3)²] ✓= -9 J ✓
Do not penalise if +3 is substituted.
(5)
[14]

QUESTION 6

6.1
v = fλ ✓
340 = 680λ ✓
λ = 0,5 m ✓
(3)

6.2

Marking criteria

If any of the underlined key words/phrases in the correct context is omitted deduct 1
mark

The change in frequency/pitch/wavelength of the sound detected by a listener because the sound source and the listener have different velocities relative to the medium of sound propagation. ✓✓

OR
An (apparent) change in observed/detected frequency/pitch/wavelength, as a result of the relative motion between a source and an observer (listener). ✓✓
(2)

6.3.1 Decreased (1)
6.3.2 Increased (1)

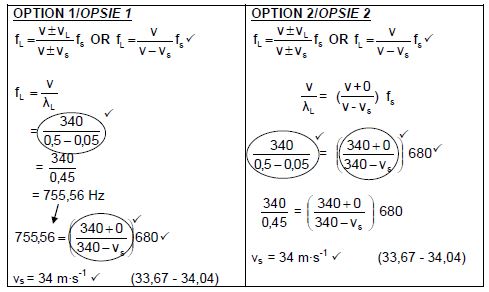
6.4 POSITIVE MARKING FROM QUESTION 6.1

(5)
[12]

QUESTION 7

7.1.1 Added ✓ (1)
7.1.2

NOTE

Ignore signs of the charges

n =Q/q_e
= - 1,95 x10^-6
- 1,6 x10^-19
= 1,22 x 10¹³ ✓ (1,21875 x 10¹³)
(3)

7.1.3

Marking criteria

If any of the underlined key words/phrases in the correct context is omitted deduct
1 mark

The (electrostatic) force experienced per unit positive charge placed at that point.

NOTE(1 mark for:)
An electric field is a region of space in which an electric charge experiences a force. (2)

7.1.4
E = kQ
r²
= (9 x 10⁹)(1,95 x 10¯⁶)
(0,5)²
= 7,02 x 10⁴ N·C^-1 ✓
(3)

7.2

OPTION 1
Marking criteria

Coulomb's Law formula
Correct substitution for F_q1 OR F_q2 into
kQ₁Q₂
r²✓
Correct substitution of 1,38 N for F(net)
Subtracting (vector addition) electrostatic forces
elektrostatiese kragte ✓
Final answer 1,11 x 10^-7 C ✓ (1,106 x 10^-7 C)

FE(net) = F_q2 + F_q1
1,38 ✓= (+ kQ₁Q₂ ) + (- kQ₁Q₂)
r²r^²
1,38 = (+ (9 x 10⁹)(1,95 x 10 )q₂) + (- (9 x 10⁹)(1,95 x 10 )q₂)
(0,03) (0,05)
q² = 1,11 x 10^-7 C ✓ (1,106 x 10^-7 C)

OPTION 2
Marking criteria

E = kQ
r²
Correct substitution of 7,08 x 10⁵ N·C^-1✓
Correct substitution for Eq₁ OR Eq₂ into
kQ₂
r²
Subtracting electric fields
Final answer 1,11 x 10^-7 C ✓ (1,106 x 10^-7 C)

E= F/q = 1,38
1,95 x 10^-6
= 7,08 x 10⁵ N∙C^-1 (707692,30)

Enet = E_q2 + E_q1
7,08 x 10⁵ = (+ kQ₂) + (- kQ₁)
r²r²
= (+ (9 x 10⁹)q₂) + (- (9 x 10⁹)q₁)
(0,03)² (0,05)²
q₂ = 1,11 x 10^-7 C ✓ (1,106 x 10^-7 C)

(5)
[14]

QUESTION 8
8.1.1 12 V ✓ (1)
8.1.2 0 (V) ✓ (1)
8.2

Marking criteria

If any of the underlined key words/phrases in the correct context is omitted deduct
1 mark

The rate at which work is done or energy is expended/transferred.
(2)

8.3

OPTION 1

P = I²R ✓
5,76 = (1,2²)R ✓
R = 4 Ω ✓

OPTION 2
P = VI
5,76 = V(1,2)
V = 4,8 V

P = V²/R✓
5,76 =(4,8)²/R✓
R = 4 Ω ✓

V = IR ✓
4,8 = (1,2)R ✓
R = 4 Ω ✓

(3)

8.4 POSITIVE MARKING FROM QUESTION 8.3

OPTION 1
1 = 1 + 1
R_p R₁ R₂

1 = 1 + 1
Rp 6 8,4

Rp = 3,5 Ω
RT = 3,5 + 4 ✓
= 7,5 Ω ✓

OPTION 2
Rp = R₁R₂
R₁+R₂

Rp = (6)(8,4)✓
6 + 8,4
Rp = 3,5 Ω
RT = 3,5 + 4✓
= 7,5 Ω ✓

(3)

8.5 POSITIVE MARKING FROM QUESTION 8.3

CALCULATE VP
Marking criteria
Formula
V = IR ✓
Substitution to calculate Vp

CALCULATE V2
Marking criteria
Substitution to calculate Ibranch or ratio
of Rbranch
Substitution to calculate V2 /
Final Answer3 V✓

OPTION 1

Vp = IR
= (1,2)(3,5) ✓
= 4,2 V

→

I = V/R
= 4,2 ✓
8,4
= 0,5 A

V₂ = IR ✓
= (0,5)(6) ✓
= 3 V ✓

OR
R_2,4 : R₆ = 2,4 : 6 ✓
= 2 : 5

V_2,4 : V₆ = 1,2 : 3 ✓✓
V₂ = 3 V ✓

OPTION 2

P_x = VI
5,76 = V(1,2)
V_x = 4,8 V
I_{6 Ω} = 8,4 x 1,2
14,4
= 0,7 A

V_{6 Ω} = IR
= (0,7)(6) ✓
= 4,2 V

→

OPTION 3
ε = I(R + r)
12 = 1,2(7,5 + r)
r = 2,5 Ω
Vp = 12 – 1,2(2,5 + 4) ✓= 4,2 V

→

CALCULATION OF I_8,4Ω AND V₂

OPTION 4
I8,4Ω = (6/14,4)(1,2)

OR
(3,5/8,4) (1,2)
= 0,5 A ✓✓

V₂ = IR ✓
= (0,5)(6) ✓
= 3 V ✓

OPTION 5

V_x = IR
= (1,2)(4)
= 4,8 V

V_ext = IR_ext
= (1,2)(7,5)
= 9 V

Vp = 9 – 4,8✓ = 4,2 V

V_8,4Ω = IR
4,2 = I(8,4)✓
I = 0,5 A

V₂ = IR ✓
= (0,5)(6) ✓
= 3 V ✓

(5)

8.6
Decreases
Total resistance decreases.
Current increases.
V_internal /Internal voltage (“lost volts”) increases ✓
V_external /external voltage decreases.

NOTE: Do not penalise if “total” is omitted. (4)
[19]

QUESTION 9

9. 1 Slip rings

ACCEPT
Split ring/slip ring commutator (1)

9. 2 Y to/na X ✓✓ (2)
9.3

Marking criteria

If any of the underlined key words/phrases in the correct context is omitted deduct
1 mark.

The AC potential difference which dissipates the same amount of energy as an equivalent DC potential difference.

ACCEPT
The DC potential difference which dissipates the same amount of energy as an equivalent AC potential difference. (2)

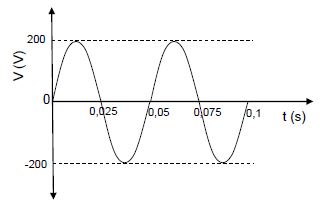
9.4

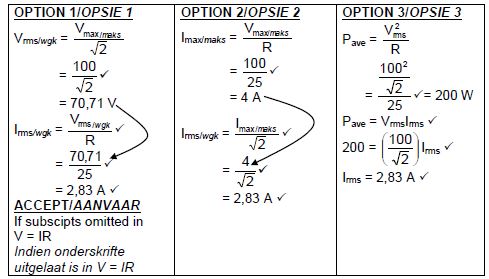
(4)

9.5 POSITIVE MARKING FROM QUESTION 9.4

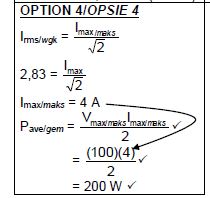
OPTION 1

P_ave = V²ᵣₘₛ
R
= 70,71²
25
= 200,00 W ✓ (200 W)

OPTION 2
P_ave= VᵣₘₛIᵣₘₛ
= (70,71)(2,83) ✓
= 200,11 W ✓

OPTION 3
Pave I²ᵣₘₛR
= (2,83)²(25) ✓
= 200,22 W ✓

9.6|

Marking criteria

2 waves ✓
2 golwe
Period of wave is 0,05 s ✓
Amplitude = 200 V ✓

(3)
[15]

QUESTION 10
10.1

Marking criteria

If any of the underlined key words/phrases in the correct context is omitted deduct
1 mark

The minimum frequency of light needed to eject electrons from a metal / surface. ✓✓(2)

10.2 Greater than ✓✓ (2)
10.3

OPTION 1

E = Wo + E_k(max) ✓
f_x = ( 1 ) (23,01x10^-19) ✓ + 10,40 x 10¹⁴ ✓
6,63 x 10^-34
= 4,51 x 10¹⁵ (Hz)✓ (45,1 x 10¹⁴ Hz )

OPTION 2

m = 1/h
fₓ - 10,4 x 10¹⁴ = 1
23,01 x 10^-19 - 0 6,63 x 10^-34
fx = 4,51 x 10¹⁵ (Hz) ✓(45,1 x 10¹⁴ Hz)

OPTION 3

E = W_o + Ek(max) ✓
hf = hf₀ + Ek(max)
6,63 x 10‾³⁴fₓ ✓= (6,63 x 10‾³⁴)(10,40 x 10¹⁴)✓+ 23,01 x 10^-19 ✓
fx = 4,51 x 1015 (Hz)✓ (45,1 x 1014 Hz )

(5)
10.4

10.4.1 No effect (1)
10.4.2 Increases(1)
10.4.3 No effect(1)

[12]
TOTAL 150

Last modified on Wednesday, 07 December 2022 07:41

Published in Grade 12 November 2021 NSC Past Exam Papers and Memos