PHYSICAL SCIENCE PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS SEPTEMBER 2016
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupPHYSICAL SCIENCE
PAPER ONE (P1)
GRADE 12
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2016
GENERAL GUIDELINES
1 CALCULATIONS
1.1 Marks will be awarded for: correct formula, correct substitution, correct answer with unit.
1.2 No marks will be awarded if an incorrect or inappropriate formula is used, even though there are many relevant symbols and applicable substitutions.
1.3 When an error is made during substitution into a correct formula, a mark will be awarded for the correct formula and for the correct substitutions, but no further marks will be given.
1.4 If no formula is given, but all substitutions are correct, a candidate will forfeit one mark.
1.5 No penalisation if zero substitutions are omitted in calculations where correct formula/principle is correctly given.
1.6 Mathematical manipulations and change of subject of appropriate formulae carry no marks, but if a candidate starts off with the correct formula and then changes the subject of the formula incorrectly, marks will be awarded for the formula and correct substitutions. The mark for the incorrect numerical answer is forfeited.
1.7 Marks are only awarded for a formula if a calculation has been attempted, i.e. substitutions have been made or a numerical answer given.
1.8 Marks can only be allocated for substitutions when values are substituted into formulae and not when listed before a calculation starts.
1.9 All calculations, when not specified in the question, must be done to a minimum of two decimal places.
1.10 If a final answer to a calculation is correct, full marks will not automatically be awarded. Markers will always ensure that the correct/appropriate formula is used and that workings, including substitutions, are correct.
1.11 Questions where a series of calculations have to be made (e.g. a circuit diagram question) do not necessarily always have to follow the same order. FULL MARKS will be awarded provided it is a valid solution to the problem. However, any calculation that will not bring the candidate closer to the answer than the original data, will no count any marks.
2 UNITS
2.1 Candidates will only be penalised once for the repeated use of an incorrect unit within a question.
2.2 Units are only required in the final answer to a calculation.
2.3 Marks are only awarded for an answer, and not for a unit per se. Candidates will therefore forfeit the mark allocated for the answer in each of the following situations:
- Correct answer + wrong unit
- Wrong answer + correct unit
- Correct answer + no unit
2.4 SI units must be used except in certain cases, e.g. V.m-1instead of N.C-1, and cm∙s-1 or km.h-1instead of m∙s-1 where the question warrants this.
3 GENERAL
3.1 If one answer or calculation is required, but two are given by the candidate, only the first one will be marked, irrespective of which one is correct. If two answers are required, only the first two will be marked, etc.
3.2 For marking purposes, alternative symbols (s, u, t etc) will also be accepted.
3.3 Separate compound units with a multiplication dot, no a full stop, for example, m∙s-1. For marking purposes, m∙s-1 and m/s will also be accepted.
4 POSITIVE MARKING
Positive marking regarding calculations will be followed in the following cases:
4.1 Subquestion to subquestion: When a certain variable is calculated in one subquestion (e.g. 3.1) and needs to be substituted in another (3.2 of 3.3), e.g. if the answer for 3.1 is incorrect and is substituted correctly in 3.2 or 3.3, full marks are to be awarded for the subsequent subquestions.
4.2 A multistep question in a subquestion: If the candidate has to calculate, for example, current in die first step and gets it wrong due to a substitution error, the mark for the substitution and the final answer will be forfeited.
5 NEGATIVE MARKING
Normally an incorrect answer cannot be correctly motivated if based on a conceptual mistake. If the candidate is therefore required to motivate in QUESTION 3.2 the answer given in QUESTION 3.1, and 3.1 is incorrect, no marks can be awarded for QUESTION 3.2. However, if the answer for e.g. 3.1 is based on a calculation, the motivation for the incorrect answer could be considered.
MEMORANDUM
QUESTION 1
1.1 C ✓✓ (2)
1.2 D ✓✓ (2)
1.3 C ✓✓ (2)
1.4 C ✓✓ (2)
1.5 B ✓✓ (2)
1.6 B ✓✓ (2)
1.7 A ✓✓ (2)
1.8 C ✓✓ (2)
1.9 D ✓✓ (2)
1.10 B ✓✓(2)
[20]
QUESTION 2
2.1 When a resultant/net force acts on an object, the object will accelerate in the direction of the force at an acceleration that is directly proportional to the force✓and inversely proportional to the mass of the object.✓
OR
The net force acting on an object is equal to the rate of change of momentum✓✓ of the object (in direction of the force). (2 or 0)
2.2 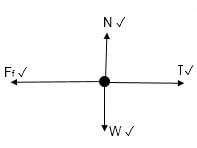 (4)
(4)
Accepted labels/Aanvaarde byskrifte | |
N | FN/ Fnormal/Normal |
T | FT/Tension |
w | Fg /Fw/weight/mg/gravitational force |
Ff | f/ friction |
Notes:
|
2.3 On 6 kg:
Fnet = ma ✓
Fg + (-T) = ma
(6 × 9,8) ✓ – T = 6 × a
58,8 – T= 6a
T = 58,8 – 6a (1)
On 4 kg:
Fnet = ma ✓
(-f) + T = ma
(-32,53) ✓ + T = 4 × a
T = 32,53 + 4a (2)
any one of the 2 above i.e (1) or (2)
(1) - (2): 0 = (58,8 – 6a) – (32,53 + 4a) ✓
a = 2,63 m∙s-2 ✓ (6)
2.4 Positive marking from QUESTION 2.3/
fk = μkN ✓ or fk = μkmg (any one)
32,53 = µk × 4 × 9,8 ✓
µk = 0,83 ✓ (3)
2.5 DECREASE ✓
At an angle of 30° the tension force will have a component in the vertical direction ✓and the block will be slightly lifted up. The normal will decrease and friction is directly proportional normal. ✓
[18]
QUESTION 3
3.1 0 m∙s-1 ✓ (1)
3.2 g = 9,8 m/s2 ✓ downwards ✓ (2)
3.3
3.3.1 (3)
OPTION 1 (downward positive) | OPTION 2 (upwards positive) |
3.3.2 (3)
OPTION 1 (Downwards is positive) | OPTION 2 (Upwards is positive) |
3.3.3
| Downwards is positive | Upwards is positive |
OPTION 1 | OPTION 2 |
OPTION 3 | OPTION 4 (4) |
OPTION 1 |
OPTION 2 |
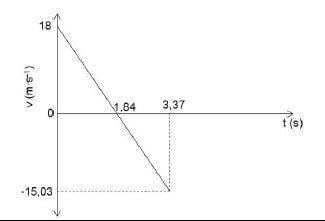
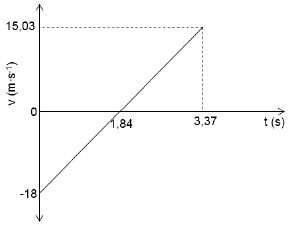
Criteria to mark the graph | Marks |
Correct shape (straight line) | ✓ |
Graph starts at v = 18 m∙s-1/-18 m∙s-1 and t = 0 s | ✓ |
Graph cuts t-axis at 1,84 s at v = 0 m∙s-1 | ✓ |
Graph shows the ball bouncing with v = -15 m∙s-1/15,03 m∙s-1 at t = 3,37 s | ✓ |
(4)
[17]
QUESTION 4
4.1 The total mechanical energy in an isolated (closed) system ✓ remains constant (is conserved). ✓
NOTE
If total or isolated/closed is omitted (max:1/2) (2)
4.2 Emech at A = Emech at B/Emeg by A = Emeg by B ✓
(mgh + ½ mv2)A = (mgh + ½ mv2)B
m (9,8 × 0,5 + ½ × 02) ✓ = m (9,8 × 0 + ½ × v2) ✓
4,9 = ½ v2
v = 3,13 m∙s-1 ✓ (4)
4.3
4.3.1 The net/total work done on an object ✓ is equal to the change in the object’s kinetic energy. ✓
OR
The work done on an object by a resultant/net force is equal ✓ to the change in the object’s kinetic energy. ✓ (2)
4.3.2 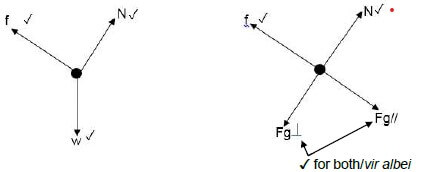 (3)
(3)
4.3.3
Wnet = ∆ EK ✓
Wnet = 0
Wf + Wg//= 0 ✓
f. ∆x ∙ cos θ+ mg. 1/∆x ∆x ∙cos θ= 0
14,7∙ d ∙cos 180°✓ + 3 × 9,8 (1/d cos 0° = 0
-14,7d + 29,4 = 0
d = 2 m ✓ (5)
4.4 REMAINS THE SAME ✓ (1)
[17]
QUESTION 5
5.1 The total( linear) momentum of an isolated (closed) system ✓ remains constant (is conserved) . ✓
OR
In a isolated (closed) system, the total(linear) momentum ✓ before collision is equal to the total linear momentum after colllision. ✓ (2)
5.2 EQUAL TO✓ (1)
5.3 Consider LEFT as positive
∑pi = ∑pf ✓ Any one
(mm + mw)vi = mvf m + mvf w
(80 + 50) × 0 ✓ = (80) vf + 50 × -4✓
vf = 2,5 m∙s-1 left ✓ (4)
5.4 (3)
OPTION 1 OR (either one) = m(vf – vi) | OPTION 2 Fnet. ∆t = ∆p ✓ OR (either one) = m(vf – vi) (3) |
[10]
QUESTION 6
6.1 The (apparent) change in frequency/ pitch of the sound ✓ detected by a listerner because the sound source and the listener have different velocities relative to the medium of sound propagation. ✓
OR
An (apparent) change in (observed/detected) frequency/pitch/wavelength ✓ as a result of the relative motion between a source and the observer /listener. ✓ (2)
6.2 As the police car is moving towards the woman, the wavelengths are compressed ✓ and become more shorter resulting in waves compressed and more waves will reach the listener per unit time, ✓ hence the frequency increases. (2)
6.3 
6.4
- Determine whether arteries are clogged/narrowed ✓
OR - Determine heartbeat of foetus ✓ (1)
6.5 AWAY ✓
Light from the distant star has a lower frequency compared to that of hydrogen. ✓ (Therefore the wavelength of the distant star is longer than the hydrogen which shows that it is shifted towards red.) (2)
[12]
QUESTION 7
7.1 The (electrostatic )force ✓ experienced per unit positive charge ✓( placed at a point) (2)
7.2
EM = kQ
r 2
= 9 × 109. QM✓ = 1 × 1013∙ QM (a)
(0,03)2
OR (either a or b)
EN = kQ
r2
= (9 × 109)(6 × 10-9 ) (b)
(0,03)2
= 540 000∙ N∙C-1
Enet = EM + (-EN ) ✓
5,2 × 105✔= 1x 10 13 ∙Qm – 540 000 ✓
5,2 × 105 + 540 000 = 1 × 1013∙QM
Qm = 2 × 10-9 C east ✓ (7)
7.3
7.3.1 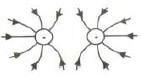 (3)
(3)
Criteria for sketch | Marks |
Correct shape | ✓ |
Correct direction | ✓ |
Field lines not crossing each other | ✓ |
7.3.2 (a) (4)
OPTION 1 |
OPTION 2 |
(b)
F = kQ1 Q2 |
(3)
[19]
QUESTION 8
8.1 Electric motor (DC motor) ✓ (1)
8.2 Electrical energy converted to mechanical energy ✓ (2)
8.3
8.3.1 Increase the strength of the current ✓ (1)
8.3.2 Parallel ✓ (1)
8.4
8.4.1 Maximum voltage✓
Accept: Vmax (1)
8.4.2
OPTION 1 Vrms = Vmax = 330 ✓ = 233,35 V | OPTION 2 Paverage = Vmax × I rms✓ |
For 8.4.2 accept range from Paverage from 2800,14 W to 2800,20 W | |
(4)
[10]
QUESTION 9
9.1
9.1.1 Rext = R1 + R2 = 6 + 6 = 12 Ω
Vext = I R ✓
10,8 ✓ = I × 12 ✓
I = 0,9 A ✓ (4)
9.1.2 POSITIVE MARKING FROM QUESTION 9.1.1 (3)
9.2
9.2.1 (7)
OPTION 1 | OPTION 2 |
OPTION 1 | OPTION 2 = 1 + 1 = 1 ✓ |
9.2.2 Increases. ✓ External resistance decreases ✓ and current increases ✓ (3)
[17]
QUESTION 10
10.1 50 × 10-19 Hz ✓ (1)
10.2 The 45 × 10-19 Hz is less than the threshold frequency of light that can eject/release electrons from the surface of the metal ✓✓ (2)
10.3
hf = W0 + ½ mv2
hf = Wo + EK ✓ ANY one
hf = hf0+ EK
(6,63 × 10-34)(110 × 10-19)✓=(6,63 × 10-34)(50 × 10-19) ✓+( × 9,11 × 10-31.v2)✓
v = 9,35 × 10-11 m∙s-1 ✓ (5)
10.4 STAYS THE SAME. ✓
Increase in the intensity increases the number of electrons emitted with the same kinetic energy. ✓ (2)
[10]
TOTAL 150