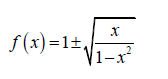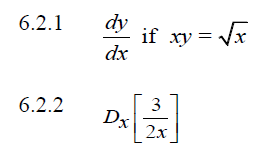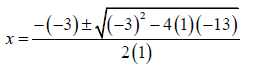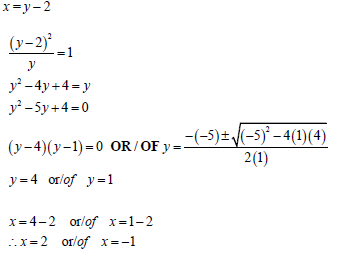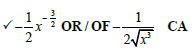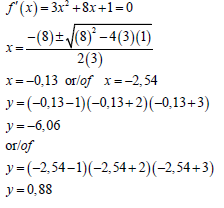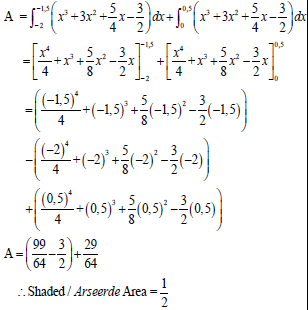MARKS: 150 

TIME: 3 hours 

INSTRUCTIONS AND INFORMATION 

Read the following instructions carefully before answering the questions.

1. This question paper consists of NINE questions. Answer ALL the questions. 

2. Clearly show ALL calculations, diagrams, graphs, etc. which you have used in  determining your answers. 

3. Answer QUESTION 4.1.4 and QUESTION 7.4 on the ANSWER SHEETS provided.  Write your name in the spaces provided and then hand in the ANSWER SHEETS with  your ANSWER BOOK. 

4. You may an use approved scientific calculator (non-programmable and non-graphical)  may be used, unless stated otherwise.  

5. If necessary, answers should be rounded off to TWO decimal places, unless stated  otherwise. 

6. Number the answers correctly according to the numbering system used in this question  paper. 

7. Diagrams are NOT necessarily drawn to scale. 

8. An information sheet with formulae is included at the end of the question paper.

9. Write neatly and legibly.

QUESTION 1 

1.1 Solve for x: 

1.1.1 3x −x²/4= 0(3)

1.1.2 x(x − 3) = 13 (Correct to TWO decimal places) (4)

1.1.3 −2x² − x + 10 ≤ 0 (Represent the solution set on a NUMBER LINE) (4)

1.2 Solve for x and y if: 

y - 2 = 2  and x² = 1
                           ^y

1.3 The diagram below shows a simple electric circuit with a light bulb, connected by a  conducting wire to a small battery.  

If : P = I²R:

1.3.1 Make I the subject of the formula. (2) 

1.3.2 Determine the amount of current flowing through the circuit if the power of  the light bulb is 5 Watts and the resistance of the conducting wire = 20 Ω. (2) 

1.3.3 Write the value of the current obtained in QUESTION 1.3.2 in Scientific  Notation. (1) 

1.4 Determine the value of A = 1010100₂ − 111011₂ in decimal form. (3) [25]

QUESTION 2 

2.1 Given: 

2.1.1 Write down the value of x for which f (x) = 1. (1)

2.1.2 Determine the values of x for which the roots of f (x) will be undefined. (3) 

2.2 Show that the roots of g(x) = 9x² - 12kx + 4k² will always be equal for all values of (4) [8] 

QUESTION 3 

3.1 Simplify the following WITHOUT using a calculator:  

3.1.1 log_xx + log_y1 (2) 

3.1.2 √18 − √128 
            5√2 (3)

3.2 Solve for x WITHOUT using a calculator: 

7^x−1 − 7^x = -2/9         HINT: log₇27 = 1,69 (7)

3.3 The Argand diagram represents the complex: . P (k ; m) is a point on z.

3.3.1 Write down the length of the modulus of z. (1)

3.3.2 Determine the length of k and m. (2)

3.3.3 Hence or otherwise, write z in rectangular form. (1) 

3.4 Solve for x y andif x − iy = 0. (2) [18]

QUESTION 4 

4.1 Given the functions f and g defined by f(x) = 3^x + 1 and g (x) = 3x + 2.

4.1.1 Write down the asymptote of f. (1)

4.1.2 Determine the coordinates of the y-intercept of f. (2)

4.1.3 Determine the x and y-intercepts of g. (3) 

4.1.4 Sketch the graph of f and g on the ANSWER SHEET provided.  
Clearly show all the intercepts with the axes and the asymptote of the graph. (6)

4.1.5 Write the coordinates of a point where the graph of g cuts the asymptote of f. (2)

4.1.6 Hence, determine the values of x for which g(x) < asymptote of f. (2) 

4.2 The diagram below represents the graphs of the functions defined by: 

• The asymptotes of k cut the graph of h at point A, its y-intercept. 
• Point B is the x-intercept of k.  

4.2.1 Write down the y-intercept of h. (1)

4.2.2 Hence, write down the value of q. (1)

4.2.3 Determine the coordinates of B. (2)

4.2.4 Write down the domain of k. (1)

4.2.5 Determine the coordinates of two points on k that are closest to point A. (4)

4.3 The graph of the function defined by: y = (x - p)² is drawn below. x = -4 and B are the x intercepts of f and A (−1 ; −5) is a turning point of f.

4.3.1 Write down the equation of the axis of symmetry. (1)

4.3.2 Determine the values of p and q. (2)

4.3.3 Calculate the coordinates of B. (2) 

4.3.4 Determine the values of x for which f(x) × f ′(x) > 0. (3) [33] 

QUESTION 5 

5.1 November 2023 Black Friday rush dropped the price of a R7 300 stamper by 11%. 

5.1.1 Calculate 11% of R7 300. (1)

5.1.2 Hence or otherwise, determine the discounted price of a stamper. (2) 

5.2 Rusting of metal is an exponential process if not attended to. The car below started  rusting 2 cm2area some years ago.  

Determine the number of years it has taken to rust 60 cm² area if the rate of rusting is  5% per year. (5) 

5.3 Ludwe invests R500 000 into an investment company that pays 7% per annum on simple  interest. At the end of the 5th year Ludwe deposits a further R77 000 into the investment  account and the interest rates changed to x% per annum, compounded monthly.  

Determine the value of x% (interest rates), if at the end of 8 years Ludwe gets a total of  R880 000 from his investment account. (6) [14] 

QUESTION 6 

6.1 Determine the derivative of f(x) = 3ax + 5 by using FIRST PRINCIPLES. (5) 

6.2 Determine: 

6.3 Determine the average gradient between points A(3 ; 5) and B (−2 ; −1). (3) [14]

QUESTION 7 

Consider: f (x) = (x – 1) (x + 2) (x + 3) 

7.1 Write down the coordinates of the x-intercept of f. (1)

7.2 Determine the y-intercept of f. (1)

7.3 Determine the coordinates of the turning point of f. (5) 

7.4 Sketch the graph of f on the ANSWER SHEET provided. Clearly indicate your turning  points and the intercepts with the axes. (4) 

7.5 Hence or otherwise, write down the values of x for which f (x) < 0. (2) [13]

QUESTION 8 

The graph below shows the path of a Boeing plane that is landing after experiencing hydraulics  problems.  

The process of its landing is observed from a certain height, in metres, over time, in seconds.

The landing path in terms of time (t) is: h(t) = h₀(0,09)^t

h(t) = Final height of descend, in metres.  
h₀ = Initial height of observation, in metres. 
t = Time of observation, in seconds. 

8.1 Write down the height of the plane, in metres, at the start of its landing observation. (1)

8.2 Determine the height of the plane after 1 second. (1)

8.3 Determine the time the plane took to drop to a height of 8,1 metres. (4)

8.4 Calculate the plane’s average speed of descend between 1 000 m to 8,1 m. (2) 

8.5 If the maximum landing speed of a plane is 290 km/h, indicate whether this plane’s  landing speed in QUESTION 8.4 was a normal speed or not. (Show your calculations.) (2) [10]

QUESTION 9 

9.1 Determine the following integrals: 

9.1.1 ∫ (−3x² + 2x^-1) dx (3)

9.1.2 ∫(x − 3) (x − 5) dx (4) 

9.2 The sketch below shows the shaded area bounded by the function g defined by: 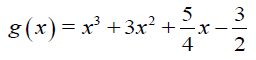 and the axis between the points where  x = − 2 and x = 1,5 together with x = 0 and x=0.5. 

Determine the area of the shaded region of the graph of g bounded by the graph and  the x-axis, between x = -2 and x = -1,5 and x = 0 and  x = 0,5. (8) [15] 

TOTAL: 150

INFORMATION SHEET: TECHNICAL MATHEMATICS 

Angular velocity =  ω = 2 π n             where n = rotation frequency

Angular velocity =  ω = 360° n            where n = rotation frequency 

Circumferential velocity= v = π Dn      where D = diameter and n = rotation frequency

Circumferential velocity= ν = ωr            where ω= Angular velocity and r = radius  

Arc length s = rθ                  where r = radius and θ = central angle in radians 

Area of a sector 2r/s      =    where r = radius, s = arc length  

MARKING GUIDELINE

MARKS/PUNTE: 150 

• If a candidate answers a question TWICE, only mark the FIRST attempt. 
• If a candidate has crossed out an attempt of a question and not redone the question, mark the crossed out version. 
• Consistent accuracy (CA) applies to ALL aspects of the marking guideline. 
• Assuming answers/values to solve a problem is NOT acceptable. 

QUESTION/VRAAG 1
1.1	1.1.1		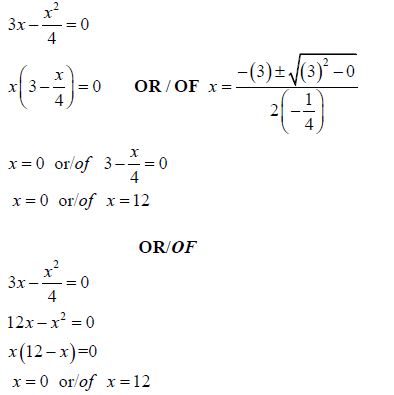✓ Factors / Substitution  Faktore / Vervanging A  ✓x = 0 CA ✓x =12 CA  (3)
	1.1.2	x (x - 3) = 13 x2 - 3x - 13 = 0  therefore: x = 5,41 or/of x = -2,41	✓ Standard Form /   Standaardvorm A ✓ SF          CA  ✓x = 5,41 CA ✓x = −2,41 CA (4)

QUESTION/VRAAG 3
3.1	3.1.1	logxx + logx 1  = 1 + 0 = 1	✓ Log property/eienskap A ✓ Log property/eienskap A (2)
	3.1.2		✓ Prime factors / Square   factors / Priemfaktore /  Vierkant faktore A  ✓ Simplification /   Vereenvoudiging CA  ✓ ‒1 CA (3)
3.2		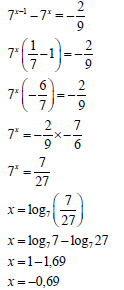	✓ Common factor / Gemene  faktor A  ✓ Simplification / Vereenvoudiging CA     ✓7xsubject / onderwerp CA  ✓ Logarithm/ Logaritme A  ✓ Log Property / eienskap CA  ✓ Substitution / Vervanging   CA  ✓ Correct value of x / Korrekte  waarde van x CA  (7)

4.2	4.2.1	y = −2	✓ y = −2 A  (1)
	4.2.2	q= −2	✓ q = −2 A (1)
	4.2.3	0 = 1/x - 2 x = 1/2	✓ y = 0 A ✓x = 1/2 CA (2)
	4.2.4	− ∞ < x < ∞ or/of  0 <  x < ∞  OR / OF  x ∈ (− ∞,0) or/of x ∈ (0,  ∞)  x ∈ R but/maar x ≠ 0	✓ Domain / def versameling A (1)
	4.2.5	x - 2 = 1/x - 2 x2 = 1 x = ±1 y = 1 - 2 or y = -1-2 y = -1 or y = -3	✓ Equating / Gelykstel A ✓ Simplification / Vereenvoudiging CA ✓ Both x values / Beide x waardes CA  ✓ Both y values / Beide y waardes CA  (4)
4.3	4.3.1	y = ‒1	✓ y = ‒1 A  (1)
	4.3.2	p = 1  en/and q = -5	✓ p = 1 A ✓ q = ‒5 A  (2)
	4.3.3		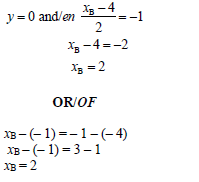✓ y = 0 A  ✓ x = 2 A  OR/OF  ✓ Equation / Vergelyking A ✓ x = 2 A   (2)
	4.3.4	‒4 < x < ‒1 or/of x > 2   OR/OF  x ∈ (-4, -1) or/of x ∈ (2,∞)   OR/OF  x > ‒ 4 and/en x < ‒1 or/of x > 2	✓ Critical values / Kritiese waardes  ✓ Notation / Notasie  ✓ x > 2   (3)
			[33]

QUESTION/ VRAAG 5
5.1.1	11% of R7 300 = R803	✓ Answer / Antwoord A (1)
5.1.2	Discounted/Afslag Stamper = R7 300 – R803 Discounted/ Afslag Stamper = R6 497	✓ M CA ✓ Answer / Antwoord CA (2)
5.2	A = P(1+ i )n 60 = 2 (1+ 0,05 )n 30 = 1.05n n = log1.0530 n = 69.71	✓ F A ✓ SF A ✓ Simplification / vereenvoudiging  CA  ✓ Logarithm / Logaritme A  ✓ n = 69,71 CA (5)
5.3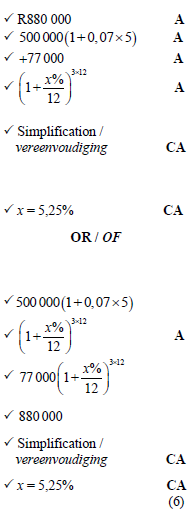
		[14]

QUESTION/VRAAG 6
6.1		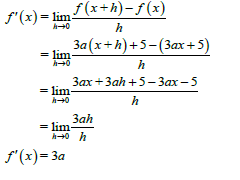	✓ Definition / Definisie A ✓ Substitution / Vervanging CA  ✓ Simplification /  Vereenvoudiging CA  ✓ Simplification /  Vereenvoudiging CA  ✓f ′ (x)= 3a  CA (5)
6.2	6.2.1		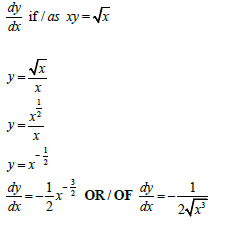✓ y subject / onderwerp A  ✓ Exponential form /  Eksponensiële vorm A  ✓ Simplification /  Vereenvoudiging CA
	6.2.2		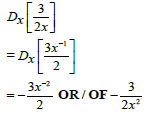✓ Simplification /  Vereenvoudiging A
6.3	Average Gradient = (y2 - y1)/(x2-x1) Average Gradient = (-1-5)/(-2-3) Average Gradient = 6/5 = 1.2		✓ F A ✓ Substitution /Vervanging A ✓6/5 OR/OF =1.2
			[14]

QUESTION/VRAAG 8
8.1	h0 =1000 m	✓ h0 =1 000 A (1)
8.2	h1 = 1000 (0.09)t h1 = 90m	✓ h1 = 90 A  (1)
8.3		✓Substitution / Vervanging A  ✓ Simplification / Vereenvoudiging CA  ✓ Logarithm / Logaritme CA  ✓ t = 2s CA (4)
8.4	Average speed = (1000 - 8.1)/(0-2) Gemiddelde spoed = 496m/s	✓ F A  ✓496 m/s A  (2)
8.5	Ave speed / = 496m/s =1786,6 km/h The plane is in a crisis of falling from the sky.	✓ 1786,6 km/h CA ✓ Conclusion / Gevolgtrekking  CA   (2)
		[10]