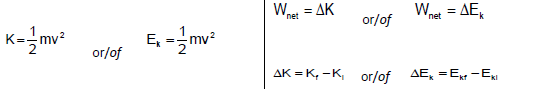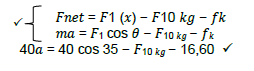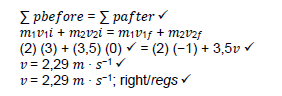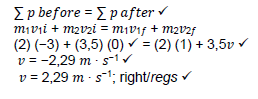MARKS: 150 

TIME: 3 hours 

INSTRUCTIONS AND INFORMATION 

Read the following instructions carefully before answering the questions.

1. Answer ALL the questions in the ANSWER BOOK. 

2. Start EACH question on a NEW page. 

3. You may use a non-programmable calculator. 

4. You may use appropriate mathematical instruments. 

5. Number the answers correctly according to the numbering system used in  this question paper. 

6. Show ALL formulae and substitutions in ALL calculations. 

7. Round off your FINAL numerical answers to a minimum of TWO decimal  places. 

8. Give brief motivations, discussions et cetera where required.

9. You are advised to use the attached DATA SHEETS. 

10. Write neatly and legibly.

QUESTION 1: MULTIPLE-CHOICE QUESTIONS 

Various options are provided as possible answers to the following questions. Choose the answer and write only the letter (A–D) next to the question numbers (1.1 to 1.10)  in the ANSWER BOOK, for example 1.11 D. 

1.1 Which ONE of the following is the best definition of acceleration?

A The rate of change of speed. 
B The rate of change of velocity.  
C The rate of change of position. 
D The rate of change of distance. (2)

1.2 The inertia of a body can be defined as … 

A the rate of change of its velocity. 
B a force acting on a string or a rope. 
C a force acting parallel to the surface and opposing motion. 
D the property of a body to resist any change in its state of motion or rest. (2) 

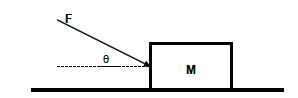
1.3 Block M is resting on a table. Force F is applied to the block as shown in the  diagram below and the block remains at rest. 

Which ONE of the following factors will NOT influence the magnitude of the  frictional force on block M? 

A The angle θ between force F and the horizontal is decreased. 
B The contact area of the block on the table is increased. 
C The magnitude of force F is decreased. 
D The mass of M is increased. (2) 

1.4 The linear momentum of an object is a … 

A vector quantity with the same direction as the velocity of the object.
B scalar quantity with the same direction as the velocity of the object. 
C scalar quantity with a direction opposite to that of the velocity of the  object. 
D vector quantity with a direction opposite to that of the velocity of the  object. (2) 

1.5 The momentum of car A changes with time just before and just after a head on collision with car B. The masses of the two cars are the same. Assume that  the system is isolated. The velocity of car B DECREASES after the collision.  

Which ONE of the following combinations about the momentum and kinetic  energy of the system is correct? 

(2) 

1.6 Power is defined as the … 

A ability to do work. 
B rate at which work is done. 
C product of mass and acceleration. 
D product of force and displacement. (2) 

1.7 A ball is thrown vertically upwards and returns to the ground. Work done by  the gravitational force on the ball is … 

A positive on its way upwards and negative on its way downwards.
B negative on its way upwards and negative on its way downwards.
C negative on its way upwards and positive on its way downwards.
D positive on its way upwards and positive on its way downwards. (2)

1.8 Which ONE of the following statements is correct? If the stress applied to a body is more than the elastic limit of the body and is  then removed, the body …  

A becomes hot.  
B opposes the stress. 
C cannot return to its original shape and size. 
D returns to its original shape and size. (2)

1.9 The pressure at a point in a liquid DOES NOT depend on the ...

A area. 
B depth. 
C density. 
D gravitational acceleration. (2) 

1.10 A light ray is directed from water to air with an angle of incidence of 0°. Which  ONE of the following is true? 

A The light ray is refracted along the normal. 
B The light ray undergoes total internal reflection. 
C The light ray is refracted towards the normal. 
D The light ray is refracted away from the normal. (2) [20]

QUESTION 2 

2.1 Mpho is pulling a suitcase with a mass of 10 kg at a CONSTANT velocity. She  pulls the suitcase over a rough, horizontal surface with a force F of 50 N at an  angle of 60° to the horizontal. 

2.1.1 State Newton’s First Law of Motion in words. (2)

2.1.2 Name the non-contact force acting on the suitcase. (1)

2.1.3 Calculate the coefficient of friction of the frictional force on the suitcase. (5) 

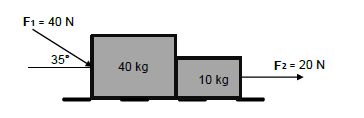
2.2 A force (F1) with a magnitude of 40 N is applied at an angle of 35° with the  horizontal on a 40 kg block standing on a ROUGH surface. The 40 kg block is  attached to a 10 kg block and a force (F2) of 20 N is applied, parallel to the  surface, on the 10 kg block. The frictional force between the 10 kg block and the  surface is 2,5 N and the frictional coefficient between the 40 kg block and the  surface is 0,04. 

2.2.1 State Newton’s Second Law of Motion in words. (2) 

2.2.2 Draw a labelled free body diagram to indicate ALL the forces acting on  the 10 kg block. (5) 

2.2.3 Calculate the magnitude of the vertical component of F1. (2)

2.2.4 Calculate the magnitude of the normal force acting on the 40 kg block. (2)

2.2.5 Calculate the frictional force acting on the 40 kg block. (4)

2.2.6 Calculate the magnitude of the acceleration of the system. (5) 

2.2.7 What will the influence be on the acceleration of the system if F2 is  applied at an angle of 30˚ with the horizontal? Only write INCREASE,  DECREASE or REMAINS THE SAME. (2) 

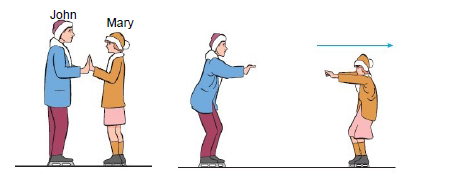
2.3 John with a mass of 70 kg, and Mary with a mass of 50 kg, are standing on an  ice rink as shown below. Then John pushes Mary away with a force of 50 N to  the right and they glide away from each other. 

2.3.1 What is the direction and magnitude of the force experienced by John  while he is pushing against Mary? (2) 

2.3.2 Explain in terms of inertia and other applicable concepts why John and  Mary would not cover equal distances from their starting points. (3) [35] 

QUESTION 3 

3.1 A cricket ball, mass 175 g, is thrown directly towards a batsman at a horizontal  velocity of 12 m∙s-1. He hits it back in the opposite direction with a velocity of  30 m∙s-1. The ball is in contact with the bat for a period of 0,05 s. 

3.1.1 Define the term impulse in words. (2) 

3.1.2 Calculate the change in momentum of the ball in magnitude and  direction. (5) 

3.1.3 Calculate the magnitude of the force exerted by the bat on the ball. (3) 

3.1.4 Modern cars use crumple zones on the front and the sides as a safety  measure to reduce injuries during a collision. Explain, by using the concept of impulse, how crumple zones reduce  injuries. (4) 

3.2 Block X, mass 2 kg, slides at 3 m∙s-1to the right and collides with a stationary  block Y, mass 3,5 kg. Block X rebounds at a velocity of 1 m∙s-1to the left. 

3.2.1 Write down the principle of conservation of linear momentum in  words. (2) 

3.2.2 Calculate the velocity of block Y after the collision. (5) [21]

QUESTION 4 

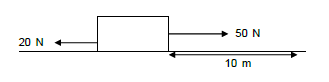
4.1 An applied force of 50 N acts on a block and it moves a distance of 10 m in a  straight line. The force of friction on the block during the motion is 20 N. 

4.1.1 Define the term work in words. (2) Calculate the: 

4.1.2 Work done by the applied force (4)

4.1.3 Work done by friction (3)

4.1.4 Net work done on the block (3) 

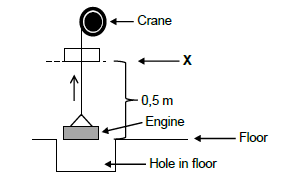
4.2 A motor mechanic stores an engine in a hole in the floor of his workshop. He  uses a crane to lift the engine out of the hole. The mass of the engine is  1 500 kg. From floor level to point X the engine moves to a height of 0,5 m at  CONSTANT velocity. The power dissipated by the crane during this distance is  7,35 kW. Ignore the mass of the cable and the effects of friction. 

4.2.1 Draw a free-body diagram to show all the forces acting on the engine  when moving between the floor and point X. (2) 

Calculate the: 

4.2.2 Speed at which the engine is lifted (4) 

4.2.3 Work done by the applied force on the engine between the floor and  point X. (3) 

4.2.4 Gravitational potential energy of the engine at point X with respect to  the floor. (3) [24] 

QUESTION 5 

A wire, length 335 cm, with a cross-sectional area of 5 x 10-5 m2, is used to  suspend a 3,5 kN weight from a horizontal beam. The weight causes the length  of the wire to increase by 12 mm. 

5.1 State Hooke’s law in words. (2)

5.2 Calculate the: 

5.2.1 Stress (3)

5.2.2 Strain (3)

5.2.3 Modulus of elasticity (3) 

5.3 Give TWO examples of perfect plastic bodies. (2) [13] 

QUESTION 6 

6.1 A 250 kg metal cylinder stands (vertically) upright on a workshop floor and the  cross-sectional area in touch with the floor is 3,15 x 104 mm². 

6.1.1 Define the term pressure. (2)

6.1.2 Calculate the pressure the cylinder exerts on the floor. (4) 

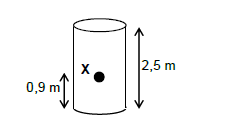
6.2 A water tank has a height of 2,5 m and is filled with water. The density of the  water is 1 000 kg·m^-3. 

6.2.1 Calculate the pressure of the water at point X in the tank. Point X is  0,9 m from the bottom of the tank. (4) 

6.2.2 The water is replaced with petrol, which has a lower density than water. Will the fluid pressure in petrol at X be GREATER THAN, LESS THAN  or the SAME AS before? Explain your answer. (4) 

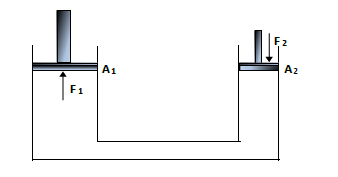
6.3 In the hydraulic lift shown below, the large piston has a cross-sectional area  (A1) of 200 cm² and the small piston has a cross-sectional area (A2) of 5 cm².  A force of 250 N is applied to the small piston. 

6.3.1 State Pascal’s law in words. (2)

6.3.2 Calculate the force F1 on the large piston. (4) 

6.3.3 Give TWO reasons why liquids, and not gasses, are preferred for use  in hydraulic systems. (2) [22] 

QUESTION 7 

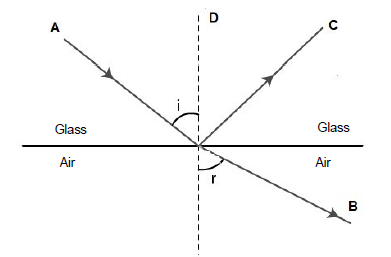
The path of a ray of light which is directed from glass to air, is shown in the diagram  below. The critical angle of the glass is 55˚. 

7.1 Define the term refraction. (2)

7.2 Label the following: 

7.2.1 A (1)

7.2.2 D (1)

7.3 Define critical angle. (2) 

7.4 What is the phenomenon called which occurs when the angle of incidence (i) is  greater than 55˚? (1) 

7.5 Will the angle of refraction (r) be GREATER THAN, SMALLER THAN or EQUAL  TO the angle of incidence (i)? (1) 

7.6 Give a reason for your answer to QUESTION 7.5. (2) 

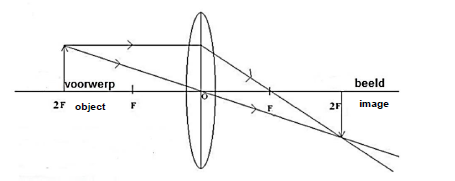
7.7 Draw a beam/ray diagram to determine the position and size of the image that  will be formed when the focal point distance F for a convex lens and an object  with a height of 3 cm is placed at a distance of 2F. (5) [15] 

TOTAL: 150 

TABLE 1: PHYSICAL CONSTANTS/TABEL 1: FISIESE KONSTANTES 

TABLE 2: FORMULAE/TABEL 2: FORMULES 

FORCE/KRAG

WORK, ENERGY AND POWER/ARBEID, ENERGIE EN DRYWING 

WAVES, SOUND AND LIGHT/GOLWE, KLANK EN LIG 

MARKING GUIDELINE

QUESTION/VRAAG 1 

1.1 B ✓✓ (2)

1.2 D ✓✓ (2)

1.3 B ✓✓ (2)

1.4 A ✓✓ (2)

1.5 A ✓✓ (2)

1.6 B ✓✓ (2)

1.7 C ✓✓ (2)

1.8 C ✓✓ (2)

1.9 A ✓✓ (2) 

1.10 A ✓✓ (2) [20]

QUESTION/VRAAG 2 

2.1

2.1.1 An object continues in its state of rest or uniform (moving with constant)  velocity ✓ unless it is acted upon by a net (resultant) force.✓ ʼn Voorwerp bly in rus of bly beweeg teen ʼn uniforme (konstante) snelheid ✓ tensy ʼn netto (resultante) krag daarop dit inwerk. ✓ (2)

2.1.2 Gravitational force/Gravitasiekrag ✓ (1) 

2.1.3 

2.2

2.2.1 When a force is exerted on an object, the object will accelerate in the  direction of the force. ✓ This acceleration is directly proportional to the  force, and indirectly proportional to the mass of the object. ✓ Indien ʼn krag op ʼn voorwerp inwerk sal die voorwerp versnel in die  rigting van die krag. ✓ Hierdie versnelling is direk eweredig aan die  krag op die voorwerp en omgekeerd eweredig aan die massa van die  voorwerp. ✓ (2) 

2.2.2 

(5) 

2.2.3

F1 (x) = F1 sin θ  = 40 sin 35 ✓ = 22,94 N ✓ (2)

2.2.4 POSITIVE MARKING FROM 2.2.3/POSITIEWE MERK VAN 2.2.3 

FN = Fg + F1 (y)  

 = mg + F1 (y) 

 = (40) (9,8) + 22,94 ✓ 

 = 414,94 N ✓ (2) 

2.2.5 POSITIVE MARKING FROM 2.2.4/POSITIEWE MERK VAN 2.2.4 

f_k = µ_k F_N

= µ_k (F_g − F1(y))  

 = (0,04) (414,94) ✓ 

 = 16,60 N ✓ left/links ✓ (4) 

2.2.6 For 40 kg block/Vir 40 kg blok 

For 10 kg block/Vir 10 kg blok 

Fnet = F40 kg + F2 - fk

ma = F40 kg + F2 - fk

10a = F40kg + 20 - 2.5

2.2.7 Increase/Neem toe ✓✓ (2)

2.3

2.3.1 50 N ✓to the left/na links ✓ (2) 

2.3.2 John’s mass is greater than Mary’s mass.  

Therefore, John’s inertia is greater than Mary’s inertia. ✓ 

John’s force on Mary is equal to Mary’s force on John ✓ 

Therefore, John’s acceleration is less than Mary’s acceleration ✓ 

QUESTION/VRAAG 3 

3.1

3.1.1 The product of the net force acting on an object ✓ and the time the force  acts on the object./ ✓ 

3.1.2 OPTION 1 Away from batsman / OPSIE 1 Weg van die kolwer

∆p = mv_f − v_i ✓ 

 = (0,175) (−30 − 12) ✓ 

 = −7,35 N ∙ s ✓ 

 = 7,35 N ∙ s ✓ away from the batsman/weg van die kolwer ✓ 

OPTION 2 Towards the batsman / OPSIE 1 Na die kolwer 

∆p = mv_f − v_i ✓ 

 = (0,175) (30 − (−12))✓ 

 = 7,35 N ∙ s ✓  

 = 7,35 N ∙ s ✓ away from the batsman/weg van die kolwer ✓ (5)

3.1.3 POSITIVE MARKING FROM 3.1.2/POSITIEWE MERK VAN 3.1.2 FnetΔt = Δp ✓ 

Fnet(0,05) = 7,35 ✓ 

FnetΔt = 147 N ✓ 

OR /OF 

FnetΔt = Δp ✓ 

Fnet(0,05) = − 7,35 ✓ 

FnetΔt = −147 N ✓ (3) 

3.1.4 ✓ if Δp is constant ✓ crumple zones increase the time ✓ Fnet decreases. ✓ 
✓ as Δp konstant is. ✓ 

3.2

3.2.1 The total linear momentum of an isolated system ✓ remains constant (in  magnitude and direction). ✓ 

3.2.2 OPTION 1 Right + / OPSIE 1 Regs + 

OPTION 2 Left + / OPSIE 2 Links + 

QUESTION/ VRAAG 4 

4.1 4.1.1 The product of the force applied on an object ✓ and the displacement in  the direction of the force. ✓ 

4.1.2 W_f = FΔxcosθ = (50) ✓(10) cos 0° ✓ = 500 j ✓ (4) 

4.1.3 W_f = FΔxcosθ = (20) ✓(10) cos180°✓ = −200 j ✓ (3) 

4.1.4 POSITIVE MARKING FROM 4.1.2 TO 4.1.3 FOR OPTION 1 

OPTION/OPSIE 1 

= 500 ✓ + (−200) ✓ 

 = 300 j ✓ 

OPTION/OPSIE 2 

Fnet = 50 − 20 = 30 N

W_net = F_net∆xcosθ

 = (30) ✓(10) cos0° ✓ 

 = 300 j✓ (3)

4.2 4.2.1 

4.2.2 P_ave = F_avev ✓ 

P_ave = mgv

7350 ✓ = (1 500)(9,8)v✓ 

v = 0,5 ms⁻¹ ✓ (4) 

4.2.3 W_f = F∆x cos θ ✓ 

W_f  = (1 500)(9,8)✓ cos 00 ✓ 

W_f = 7350 j ✓ (3) 

4.2.4 E_p = mgℎ✓ 

 E_p = (1 500)(9,8)(0,5)✓ 

 E_p = 7 350 j ✓ (3) [24] 

QUESTION/VRAAG 5 

5.1 Within the limit of elasticity, stress is directly proportional to strain ✓✓/ Binne die grense van elastisiteit is druk eweredig aan rekking ✓✓ (2) 

5.2

5.2.1 δ = F/A✓ 

δ = 3 500
     5 × 10^-5 ✓ 

δ = 7 × 10⁷Pa ✓ (3)

5.2.2 ε =∆lL✓ 

ε =12 

3 350✓ 

ε = 3,582 ×10^-3 ✓ (3) 

5.2.3 POSITIVE MARKING FROM /POSITIEWE MERK VAN 5.2.1 and/en 5.2.2 

K =∂ε✓ 

K =7 × 10⁷ 
    3,582 ×10^-3 ✓ 

K = 1,95 × 10¹⁰ Pa ✓ (3) 

5.3 Clay, putty, wax, bread dough (any TWO) ✓✓/ 

QUESTION/VRAAG 6 

6.1

6.1.1 It is the thrust acting on the unit area around that point. ✓✓/ Dit is die stukrag op die eenheidsoppervlakte rondom daardie punt ✓✓ (2) 

6.1.2 P =FA✓ 

P =(250)(9,8) ✓ 
 (3,15 ×10⁴)(10)⁶ ✓ 

P = 7,78 × 10⁴Pa ✓ (4)

6.2

6.2.1 P = ρgh ✓ 

P = (1 000)(9,8) ✓ (2,5 − 0,9) ✓ 

P = 1,57 ×10⁴Pa ✓ (4) 

6.2.2 Less Than / Minder as ✓ 

From/Van P = h ✓ 

P α ρ ✓ if g and h are constant/Indien g en h konstant is 

ρ_petrol < ρ_water ✓ (4) 

6.3

6.3.1 In a continuous liquid at equilibrium, the pressure applied at a point ✓ is transmitted equally to the other parts of the liquid. ✓ 
In ʼn kontinue vloeistof by ewewig is die druk wat by enige punt toegepas word ✓ eweredig na die ander dele van die vloeistof versprei. ✓ (2) 

6.3.2 F1    F2 
         A1=  A2✓ 

       F1                 250       
200 × 10^-4 ✓ =  5 × 10^-4 ✓ 

F1 = 10 000 N ✓ (4) 

6.3.3 Liquid adapts to the form of the container.  

Liquid is not compressible. (Any TWO ✓✓) 

Liquid applies pressure in all directions.  

QUESTION/VRAAG 7 

7.1 The bending of light when it passes from one medium to another. ✓✓

7.2

7.2.1 Incident ray/Invalsstraal ✓ (1)

7.2.2 Normal/Normaal ✓ (1) 

7.3 The angle of incidence in the denser medium ✓such that the refracted ray just passes through the surface of separation of the two mediums. ✓ 

OR 

The angle of incidence in the optically dense medium ✓ for which the angle  of refraction is 90˚. ✓ 

7.4 Total Internal Reflection/Totale Interne Weerkaatsing ✓ (1)

7.5 GREATER THAN / GROTER AS ✓ (1) 

7.6 The ray moves from a more dense to a less dense medium ✓and will therefore  be refracted away from the normal ✓ which will increase the angle. 

7.7 

Marking guidelines/Nasienriglyne 

• Object at 2F / Voorwerp by 2F ✓ 
• Image at 2F / Beeld by 2F ✓ 
• Ray goes through optic centre / Straal gaan deur optiese middelpunt ✓
• Ray parallel with main axis / Straal parallel aan die hoof-as ✓ 
• Image the same size as object / Beeld net so groot soos die voorwerp ✓ (5) [15] 

TOTAL/TOTAAL: 150