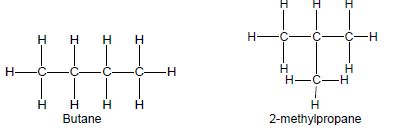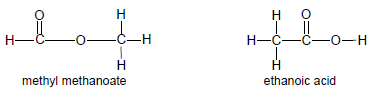TECHNICAL SCIENCES GRADE 12 - EXAMINATION GUIDELINES 2021
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupTECHNICAL SCIENCES
EXAMINATION GUIDELINES
GRADE 12
2021
| TABLE OF CONTENTS | Page |
| 1. INTRODUCTION | 3 |
| 2. ASSESSMENT IN GRADE 12 2.1 Grade 12 Programme of Assessment for Technical Sciences 2.2 Format of final examination question papers 2.3 Numbering and sequence of questions 2.4 Weighting and description of cognitive levels 2.5 Weighting of topics for Final and Preparatory (Trial) Examinations in Grade 12 2.6 Skills in Technical Sciences 2.7 Prior knowledge from Grades 10 and 11 | 4 4 5 6 6 6 7 7 |
| 3. ELABORATION OF THE CONTENT FOR GRADE 12 (CAPS) 3.1 Paper 1 3.2 Paper 2 | 8 8 17 |
| 4. GENERAL INFORMATION 4.1 Quantities, symbols and units 4.2 Information sheets – Paper 1 4.3 Information sheets – Paper 2 4.4 Assessment taxonomy for Technical Sciences | 25 25 27 29 33 |
| 5. MARKING GUIDELINES: PAPER 1 5.1 Calculations 5.2 Units 5.3 General 5.4 Positive marking 5.5 Negative marking | 35 |
| 6. MARKING GUIDELINES: PAPER 2 6.1 Calculations 6.2 Units 6.3 General 6.4 Positive marking 6.5 Negative marking | 37 37 37 37 38 39 |
| 7. CONCLUSION | 39 |
1. INTRODUCTION
The Curriculum and Assessment Policy Statement (CAPS) for Technical Sciences outlines the nature and purpose of the subject. This guides the philosophy underlying the teaching and assessment of the subject in Grade 12.
The purpose of these Examination Guidelines is to:
- Provide clarity on the depth and scope of the content to be assessed in the Grade 12 National Senior Certificate (NSC) Examination in Technical Sciences.
- Assist teachers to prepare learners adequately for the examinations.
This document deals with the final Grade 12 external examinations. It does not deal in any depth with the School-Based Assessment (SBA).
These examination guidelines should be read in conjunction with the following document:
- The National Curriculum Statement (NCS) Curriculum and Assessment Policy Statement (CAPS): Technical Sciences
2. ASSESSMENT IN GRADE 12
2.1 Grade 12 Programme of Assessment for Technical Sciences
| Programme of Assessment for Technical Sciences Grade 12 | ||||||||
| Assessment Tasks | Term 1 | Term 2 | Term 3 | Term 4 | % of Final Promotion Mark | Marks | ||
| SBA | Control Test 1 (35% of SBA) | 1 paper | 8.8 | 25% | The marks of all three tasks are converted according to the weighting to give a total mark out of 100 | |||
| Preparatory examination (65% of SBA) | 2 papers | 16.2 | ||||||
| PAT | Experiment 1 (40% of PAT) | 1 | 10 | 25% | The marks of all three tasks are converted according to the weighting to give a total mark out of 100. | |||
| Experiment 2 (30% of PAT) | 1 | 7,5 | ||||||
| Experiment 3 (30% of PAT) | 1 | 7,5 | ||||||
| External Examination | 2 Final Examination papers | 2 papers | 50 | 50% | 2 papers Paper 1 of 150 marks for 3 hours. Paper 2 of 75 marks for 1,5 hours. 150 marks + 75 marks give a total of 225 marks overall for Papers 1 and 2. The 225 marks are converted to 200 marks. | |||
| Final Promotion Mark | 100% | SBA + PAT + Final Examination = 100 + 100 + 200 = 400 | ||||||
Weighting for the SBA, PAT and Final Examinations for Grade 12
Formal assessment marks
| Description | Weighting | Maximum Marks (after conversion) |
| SBA | 25% | 100 marks |
| PAT | 25% | 100 marks |
| Final Examinations | 50% | 200 marks |
| Programme of Assessment | 100% | 400 marks |
The table below shows the compilation of the mark for school-based assessment (SBA).
| Description | Time frame | Weighting in terms of final SBA mark | Marks |
| Control Test 1 | Term 1 | 35% | 100 converted to 35 |
| Trial Examinations | Term 3 | 65% | 225 converted to 65 |
| Total SBA mark | 100% | 100 marks |
2.2 Format of final examination question papers
| Paper | Type of questions | Duration | Maximum Marks | Date | Marking |
| 1 | 10 multiple-choice questions (20 marks) Either 8 matching items questions or 8 one-word questions (8 marks) Structured questions (122 marks) | 3 hours | 150 | October/November | External |
| 2 | 5 multiple-choice questions (10 marks) Either 4 matching items questions or 4 one-word questions (4 marks) Structured questions (61 marks) | 1,5 hours | 75 | October/November | External |
- 2.3 Numbering and sequence of questions
QUESTION 1 for PAPER 1: Multiple-choice questions
Subquestions numbered 1.1 to 1.10 (2 marks each)
Questions will be arranged from lower to higher cognitive levels (easier to more challenging) and may cover all cognitive levels. - QUESTION 1 for PAPER 2: Multiple-choice questions
Subquestions numbered 1.1 to 1.5 (2 marks each)
Questions will be arranged from lower to higher cognitive levels (easier to more challenging) and may cover all cognitive levels. - QUESTION 2 onwards for both PAPER 1 and PAPER 2:
Longer questions assessing skills and knowledge across cognitive levels. These questions may include 8 one-word questions or matching items questions (8 marks) in Paper 1 and 4 one-word questions or matching items questions (4 marks) in Paper 2.
Numbering starts with QUESTION 2 and will be continuous. Subquestions will be numbered with two digits, e.g. 2.1, 2.2. Numbering is restricted to a maximum of three digits, e.g. 2.1.1, 2.1.2.
2.4 Weighting and description of cognitive levels
Papers 1 and 2 will include questions across four cognitive levels. The distribution of cognitive levels in Paper 1 and Paper 2 is given below. (Ref: 2021 Grade 12 CAPS Amendments Abridged Section 4.)
All assessment tasks should comply with the cognitive levels given in the table below.
| Cognitive levels | Description | % Weighting for Paper 1 | % Weighting for Paper 2 |
| 1 | Remembering | 25 | 30 |
| 2 | Understanding | 30 | 35 |
| 3 | Analysing and applying | 40 | 30 |
| 4 | Creating and evaluating | 5 | 5 |
2.5 Weighting of topics for Final and Preparatory (Trial) Examinations in Grade 12
(Ref.: 2021 Grade 12 CAPS Amendments Abridged Section 4)
| Paper 1 | ||||||||
| Content | Marks | % Weighting | Total | Duration | Weighting of questions across cognitive levels | |||
| Mechanics | 93 | 62 | 150 marks | 3 hours | 25 | 30 | 40 | 5 |
| Electricity and Magnetism | 33 | 22 | ||||||
| Waves, Sound and Light | 24 | 16 | ||||||
| Paper 2 | ||||||||
| Content | Marks | % Weighting | Total | Duration | Weighting of questions across cognitive levels | |||
| Matter and Materials | 47 | 62 | 75 marks | 1,5 hours | 30 | 35 | 30 | 5 |
| Chemical Change | 28 | 35 | ||||||
Marks and duration for examination papers in Grade 12
| Examination | Maximum marks | Duration |
| Mid-year Examinations | ||
| Paper 1 | 150 | 3 hours |
| Paper 2 | 75 | 1,5 hours |
| Preparatory Examinations | ||
| Paper 1 | 150 | 3 hours |
| Paper 2 | 75 | 1,5 hours |
| Final Examinations | ||
| Paper 1 | 150 | 3 hours |
| Paper 2 | 75 | 1,5 hours |
2.6 Skills in Technical Sciences
The main skills are practical application and observing simulations.
These skills can be acquired through:
- Classifying
- Communicating
- Measuring
- Designing an investigation
- Drawing and evaluating conclusions
- Formulating models
- Hypothesising
- Describing, explaining, arguing the validity of a statement/event using scientific principles
- Identifying and controlling variables
- Observing and comparing
- Interpreting, e.g. graphs, results, patterns, relationships, etc.
- Predicting
- Problem-solving and reflecting
2.7 Prior knowledge from Grades 10 and 11
All skills and application of knowledge learnt in Grades 10 and 11 are applicable to assessment in Grade 12. In addition to content from Grades 10 and 11 included under examinable content for Grade 12, skills, and knowledge from Grades 10 and 11 that may be assessed in Grade 12 include the following:
- The use of equations in solving problems
- Content knowledge acquired in Grades 10 and 11
- Context applicable to Technology
NOTE: Although there might be no direct questions about these aspects, applications thereof maybe assessed.
3. ELABORATION OF THE CONTENT FOR GRADE 12 (CAPS)
The final examination in Technical Sciences will cover the topics outlined below. This section must be read in conjunction with the Technical Sciences Curriculum and Assessment Policy Statement.
3.1 Paper 1
| Newton's Laws and Application of Newton's Laws (This section must be read in conjunction with the CAPS, p. 19, 30 and 40.) |
Different kinds of forces: weight, normal force, frictional force, applied force (push, pull), tension (strings or cables)
- Describe weight as the gravitational force the Earth exerts on any object on or near its surface.
- Calculate weight using the expression w = mg.
- Define normal force, N, as the perpendicular force exerted by a surface on an object that lies on that surface. (Grade 10)
- Define frictional force, Ff, as the force parallel to the surface that opposes the motion of object and acts in the direction opposite motion the object. (Grade 10)
- The static (limiting) frictional force acts between the two surfaces when the object is stationary. It is given by s s N f F . (Grade 11)
- The kinetic (dynamic) frictional force acts between the two surfaces when the object is moving. It is given by k k N f F . (Grade 11)
- Define tension, T, as a force acting on a string or rope. (Grade 10)
- Distinguish between mass and weight.
- Given a force, F, acting at an angle to the horizontal axis, resolve the force into its parallel and perpendicular components (Rectangular components) (Grade 11)
Force diagrams, free-body diagrams
- Define a force diagram.
- Define a free-body diagram.
- Draw force diagrams.
- Draw free-body diagrams.
- Draw force diagrams and free-body diagrams for objects that are in equilibrium or accelerating.
- Determine the resultant or net force of two or more forces.
Newton's First, Second and Third Laws
- State Newton's First Law: An object continues in a state of rest or uniform (moving with constant) velocity unless it is acted upon by a net (resultant) force.
- Define inertia as the property of a body to resist any change in its state of motion or rest.
- Define mass as a measure of the inertia of a body.
- Give examples to illustrate Newton's Fist Law.
- Discuss why it is important to wear seatbelts, using Newton's First Law.
- Define acceleration as the rate of change of velocity.
- State Newton's Second Law: When a net/resultant force is applied to an object of mass, m, it accelerates the object in the direction of the net force. The acceleration is directly proportional to the net/resultant force and inversely proportional to the mass of the object.
- Use the equation, Fnet = ma, to solve problems involving force, mass and acceleration in the content of technology. (Do not include pulley problems and lift problems.)
- Apply Newton's laws to a variety of equilibrium and non-equilibrium problems including:
- A single object:
- Moving on a horizontal plane with or without friction
- Moving in the vertical plane
- Two-body systems (joined by a light inextensible string):
- Both on a flat horizontal plane with and without friction
- A single object:
- State Newton's Third Law: When object A exerts a force on object B, object B
simultaneously exerts an oppositely directed force of equal magnitude on object A. - Identify and give examples of action-reaction pairs.
- List the properties of action-reaction pairs.
| Momentum and Impulse (This section must be read in conjunction with the CAPS, p. 41) |
Momentum
- Define momentum as the product of an object's mass and its velocity.
- Describe linear momentum as a vector quantity with the same direction as the velocity of the object.
- Calculate the momentum of a moving object using p = mv, in the context of technology.
Newton's Second Law in terms of momentum
- State Newton's Second Law of Motion in terms of momentum: The net (or resultant) force acting on an object is equal to the rate of change of momentum of the object in the direction of the net force.
- Net force is equal to the rate of change in momentum, Fnet= Δp
Δt - Calculate the change in momentum when a resultant force acts on an object and its velocity:
- Increases in the direction of motion, e.g. 2nd stage rocket engine fires
- Decreases, e.g. brakes are applied
- Reverses its direction of motion, e.g. a soccer ball kicked back in the direction it came from
Impulse
- Define impulse as the product of the net force acting on an object and the time the net force acts on the object.
- Impulse is equal to the change in momentum.
- Use the impulse-momentum theorem: FnetΔt = mΔV, to calculate the force exerted, the time for which the force is applied and the change in momentum for a variety of situations involving the motion of an object in one dimension in the context of technology.
- Explain how the concept of impulse applies to road safety considerations in everyday life, e.g. airbags, seatbelts, crumple zones and arrestor beds.
- Conservation of momentum and elastic and inelastic collisions
- Explain what is meant by:
- An isolated system (in Physics): An isolated system is one on which the net external force acting on the system is zero.
- Internal and external forces
- State the principle of conservation of linear momentum: The total linear momentum of an isolated system remains constant (is conserved) in magnitude and direction.
- Use the conservation of momentum to solve problems involving momentum in the context of technology (restrict problems to two objects moving in one dimension along a straight line with the aid of an appropriate sign convention).
- Distinguish between elastic collisions and inelastic collisions using:
- Word statements
- Calculations
| Work, Energy and Power (This section must be read in conjunction with the CAPS, p 21, p. 41– 42.) |
Work
- Define the work done as the product of the applied on an object and the displacement in the direction of the force.
- Work is a scalar quantity (as it is the product of two vector quantities).
- Use the equation, W = FΔXcosθ to solve problems involving force, work done and displacement (where a force, F, and the displacement, ΔX are at an angle, Δ, to each other).
- Explain that no work is done when a force acts at right angles to the direction of motion.
- Draw a force diagram and free-body diagrams.
- Calculate the net work done on an object using the equation, Wnet = FnetΔXcosθ.
- Define energy as the ability to do work.
- Emphasise that both work and energy are scalar quantities and have a SI unit, joule (J).
Energy and conservation of mechanical energy
- Define gravitational potential energy of an object as the energy it has because of its position from the surface of the Earth. (Grade 10)
- Do calculations using Ep = mgh or U = mgh.
- Define kinetic energy as the energy of an object due to its motion. (Grade 10)
- Do calculations using Ek = ½ mv2 or K = ½ mv2.
- Define mechanical energy as the sum of the gravitational potential energy and kinetic energy. (Grade 10)
- Solve energy problems using the equation: ME = Ek + Ep (where ME is mechanical energy, Ek is kinetic energy and Ep is potential energy).
- State the principle of conservation of mechanical energy: The total mechanical energy (sum of gravitational potential energy and kinetic energy) in an isolated system remains constant. A system is isolated when the net external force (excluding the gravitational force) acting on the system is zero.
- Solve conservation of mechanical energy problems using the equation: ME = Ek + Ep (where ME is mechanical energy, Ek is kinetic energy and Ep is potential energy).
- Use the equation above to solve problems involving kinetic energy, potential energy and velocity in one dimension only.
Power
- Define power as the rate at which work is done or energy is expended.
In symbols: P = W where P is power, W is work done and Δt is change in time or time taken. Also P = E where E is energy.
Δt Δt - Power has the SI unit, watt, W.
- Calculate the power involved when work is done.
- Practical units of power in the context of technology:
- kW = 1000 W
- Horse power (hp) = 746 W
- Solve problems involving work, power and time, with the emphasis on conversions of the practical units.
- Perform calculations using Pave= F·vave when an object moves at a constant speed. Calculate the power output for a pump lifting a mass (e.g. lifting water through a height at constant speed).
- Solve problems involving power, force and velocity, with the emphasis on conversions of the practical units.
| Elasticity, Viscosity and Hydraulics (This section must be read in conjunction with the CAPS, p. 43–44.) |
- Elasticity
- Define a deforming force as a force that changes the shape and size of a body.
- Define restoring force as a force that is equal and opposite to the deforming force applied (to a body).
- Explain that when a deforming force is applied to a body, the restoring force develops inside the body to oppose the effect of the deforming force, thus restoring its original size and shape of that body.
- Elasticity of a body is a property of the body by virtue of the body regains its original shape and size when the deforming force is removed.
- Define a perfectly elastic body as a body which regains its original shape and size completely when the deforming force is removed. Some of the examples of a perfectly elastic body are quartz fire in guitar strings and phosphorus bronze in springs and cables.
- Define a perfectly plastic body is a body that does not show a tendency to regain its original shape and size when the deforming force is removed. Examples of a perfectly plastic body are wax, putty, etc.
- Elastic limit is the maximum force that can be applied to the body so that the body regains its original form completely on removal of the force.
- Stress is internal restoring force per unit area of a body.
Stress has the SI unit Pa or N·m-2.
σ= F where σ is stress, F is force and A is area.
A - Use the equation above to calculate stress, force and area or diameter.
- Strain is the ratio of change in dimension to the original dimension.
ε = ΔL where ε is strain, ΔL is the change in length and L is the original length.
L
Strain does not have a unit. - Hooke's law states that, within the limit of elasticity, stress is directly proportional to the strain.
- Stress α strain.
∴ σ = K where K is a constant known as Young's modulus of elasticity of a material of a body. (Young's modulus of elasticity referred to as modulus of elasticity.)
ε
K has the unit N·m-2 or Pa. - Use the equation above to calculate stress, strain and modulus of elasticity.
- Young's modulus of elasticity is measure of the ability of material to withstand changes in length when subjected to lengthwise tension or compression. It is a measure of stiffness.
Explain that materials with higher modulus will be less deformed under load compared to those with lesser modulus. During repairs, use materials with similar modulus like the original material to allow uniform load transfer across the repaired section.
Viscosity
- Define viscosity as the property of the fluid to oppose relative motion between the two adjacent layers.
- Discuss the effect of temperature on viscosity in the field of technology.
- Explain that, as the temperature of the fluid increases, its viscosity decreases. The liquids used as the lubrication fluid and for number of other applications should be selected properly considering the operating temperatures.
- Discuss motor oil viscosity grades.
Hydraulics
- Hydraulics (fluid mechanics) is a field in applied sciences and engineering dealing with mechanical properties of liquids.
- Applications of hydraulics principles include:
- Designing hydraulic systems, steering systems, brake systems, power-assisted steering, etc.
- Presses: metal presses, wood presses, ceramic presses, plastic presses, etc.
- Machines for industries: metal, wood, textile, paper, etc.
- Processing machinery: wood processing machinery, sheet metal processing machinery, etc.
- Casting: foaming, blowing, extruding machines, etc.
- Component finishes: circular tables, revolving distributors, clamping systems, etc.
- Define thrust as the normal force exerted by a liquid at rest on a given surface in contact with it.
- Define pressure at a particular point as the thrust acting on the unit area around that point.
The SI unit for pressure is N·m-2 or Pascal (Pa). - Use the equation, Pressure = Thrust = F to calculate pressure, thrust and area.
Area A - Use the following conversions in all calculations:
- 1 atmosphere (atm) = 1,0110 x 105 Pa
- bar: 1 bar = 105 Pa
- torr: 1 torr = 133 Pa
- Fluid pressure is given by the following equation: P =ρ g h, where P is pressure, ρ is density, g is gravitational acceleration and h is height.
- Use the equation, P = g h to calculate fluid pressure, height and density.
- The pressure exerted by a static fluid depends only upon the depth of the fluid, the density of the fluid, and the acceleration of gravity. The fluid pressure at a given depth does not depend upon the total mass or total volume of the liquid.
- Pascal's law states that in a continuous liquid at equilibrium, the pressure applied at a point is transmitted equally to the other parts of the liquid. This law is the basic principle that causes hydraulic power in heavy construction machines to work.
- Applications of Pascal's law include: bulldozer's working system, hydraulic power brakes on automobiles, dentists' chairs, hydraulic lifts used to lift heavy loads, car jacks, etc.
- The equation for hydraulic lifts: F1 = F2 where A is the area and F is the force A2 > A1.
A1 A2 - Use the equation above to calculate force, area and radius of the piston.
| Electricity and Magnetism: Electrostatics (This section must be read in conjunction with the CAPS, p. 50.) |
Capacitors and capacitance
- Define a capacitor as a device for storing electrical charge.
- The capacitor is made of two plates separated by a dielectric (insulating) material.
- Examples of capacitors used in technology:
- Filter circuits in power supplies
- Separation of frequencies between the woofer (base) speaker and tweeter (high pitch) speaker/electronic noise filtering
- Power factor correction/improvement in electrical transmission systems
- Capacitance, C, of a capacitor is the amount of charge it can store per volt.
The SI unit for capacitance is F (farad). - 1 F = 1 C·V-1
- The relationship between the capacitance, C, charge, Q, and voltage, V, is: C = Q where C represents capacitance, Q is the charge, and V is the voltage.
V - Use the equation above to calculate the capacitance, charge and voltage between the plates.
- The capacitance can also be expressed as: C = κεoA where A is the area of the plates, d is the distance between the plates, κ is relative permittivity of free space d
(or dielectric constant of material used) and εo is the permittivity for free space. - In case dielectric material is air, vacuum or is not mentioned, the equation can be rewritten as follows: C =εoA where κ = 1 and εo = 8,85 x 10-12 F·m-1.
d - Use the equation above to calculate the capacitance, area and distance between the plates.
- Discuss the factors affecting capacitance.
| Electric Circuits (This section must be read in conjunction with the CAPS, p. 25, 26, 36 and 51.) |
Grade 10
- Define current, I, as the rate of flow of charge. It is measured in Ampere (A).
- Define terminal potential difference in terms of work done and charge. V = W/Q
- Give the difference between emf and terminal potential difference.
- Define resistance as the opposition to the flow of electric current.
- State and explain factors that affect the resistance of a substance.
Ohm's law (Grade 11)
- State Ohm's law in words: The potential difference across a conductor is directly proportional to the current in the conductor at constant temperature.
- Determine the relationship between current, voltage and resistance at constant temperature using a simple circuit.
- State the difference between ohmic and non-ohmic conductors and give examples of each.
- Solve problems using R = V for series and parallel circuits (maximum four resistors).
I - Use series and parallel resistors in combination with Ohm's law.
- Define emf as the potential difference across a cell when the circuit is open.
- Define internal resistance as the resistance inside the cell when current flows through it. (No calculations needed).
- Power, energy
- Define power as the rate at which electrical energy is converted in an electric circuit.
The SI unit for power is watt, W.
The practical unit of power is kWh. - Solve problems using P = W , P= VI, P = 12R or P =V2 to calculate power, work/energy, time, voltage, current and resistance.
Δt R - Deduce that the kilowatt hour (kWh) refers to the use of 1 kilowatt of electricity for 1 hour.
- Calculate the cost of electricity usage given the power specifications of the appliances used as well as the duration if the cost of 1 kWh is given.
- The heat produced by the resistor in a circuit is given by: W = I2Rt
Electromagnetism (This section must be read in conjunction with the CAPS, p.52–54.) |
- A current carrying conductor produces a magnetic field around it.
- Determine the direction of the magnetic field around the current carrying conductor (using the right-hand rule).
- Draw the magnetic field lines around a:
- Straight current carrying wire/conductor
- Current carrying loop (single) of wire
- Define electromagnetic induction as the production of an electromotive force (emf) or voltage across an electrical conductor due to relative motion between the conductor and magnetic field OR the process of generating electricity from motion.
- Define magnetic flux as the number of field lines perpendicular to the given surface.
- The SI unit for magnetic flux is weber, Wb.
- Φ= B A, where Φ is magnetic flux, B is magnetic flux density and A is the area of a loop.
- Use the equation above to calculate magnetic flux, magnetic flux density and area of a loop.
- Define magnetic flux density as the number of field lines per unit area.
The SI unit for magnetic flux density is tesla, T.
1 T = 1 Wb·m-2 - B = Φ where Φ is magnetic flux, B is magnetic flux density and A is the area of a loop
A - Faraday's law states that when the magnetic flux linked with the coil changes, an emf is induced in the coil. The magnitude of the induced emf is directly proportional to the rate of change of the magnetic flux.
- ε = -N ΔΦ, where is generated/induced emf, N is the number of coils (turns), Φ is magnetic flux and t is time.
Δt
NOTE: The negative sign indicates that the emf is in the opposite direction to the effect that produces it. - Use the equation above to calculate the emf, number of turns/coils, magnetic flux and time.
- Lenz's law states that the direction of the induced emf in the coil opposes the effect that produces it.
- Use examples from technology to demonstrate Lenz's law.
- Define a transformer as a device used to set up or step down the voltage.
- The output voltage is determined by the number of turns in the primary and secondary coils as well as the input voltage: VS = NS
Vp Np - Use the equation above to determine the input voltage, output voltage and number of turns in the primary and secondary coils.
- A transformer that increases the voltage is called a step-up transformer.
In a step-up transformer, Np < Ns. - A transformer that decreases the voltage is called a step-down transformer.
In a step-down transformer, Np > Ns. - Define a generator as the device that converts mechanical energy into electrical energy.
- State the energy conversion in generators.
- Explain the basic operational principles of an AC generator (alternator).
- Explain how a DC generator works and how it differs from AC generator.
- State the advantages of alternating current over direct current.
- Sketch graphs of voltage vs. time and current vs. time for an AC circuit.
- Use the principle of electromagnetic induction to explain how a generator works.
- Explain the functions of the components of an AC and a DC generator.
- State examples of the uses of AC and DC generators.
- Define a motor as a device that converts electrical energy into mechanical energy.
- State the energy conversion in motors.
- Explain the basic operational principles of an electric motor.
- Use the motor effect to explain how a motor works.
- Explain the functions of the components of a motor.
- State examples of the use of a motor.
| Waves, Sound and Light (This section must be read in conjunction with the CAPS, p. 48–49.) |
Light
Define the following terms:
- Wave: a disturbance that transfers energy through matter or space
- Reflection: the change in direction of a wave upon striking the interface between two materials
- Refraction: the bending of light when it passes from one medium to another
- Critical angle: the angle of incidence in the denser medium such that the refracted ray just passes through the surface of separation of the two media OR the angle of incidence in the optically dense medium for which the angle of refraction is 90°.
- Dispersion: the phenomenon whereby light breaks up into its component colours
Discuss the following:
- Laws of reflection
- Laws of refraction
- The relationship between the speed of light and the wavelength when it passes through media of different optical densities
- Total internal reflection: When the angle of incidence is greater than the critical angle, the ray of light reflects into the original medium.
- Discuss the conditions of total internal reflection.
- State uses of total internal reflecting prisms.
Lenses
- Discuss the frequency and wavelength of the various components of light.
- Differentiate between a concave and a convex lens.
- Discuss and draw the ray diagram to show the transmission of light through convex and concave lenses. The ray diagrams should indicate: principal axis, optic axis, focal length and focal point. Principal axis is a straight line perpendicular to the surface of the lens and passes through the optic axis. The central horizontal line that passes through centres of curvature of lens surfaces is called the optic axis.
- The focal length is the distance between the focal point (f) and the centre of the lens. It is always of the same length on both sides of the lens. The focal point of a lens is the point in space where parallel light rays meet after passing through the lens.
- Discuss applications of convex and concave lenses.
- Give the properties of images formed by concave and convex lenses.
Electromagnetic radiation
- Define an electromagnetic wave as a changing magnetic and electric field mutually perpendicular to each other and the direction of propagation of the wave.
- Discuss properties of electromagnetic waves.
- Use the equation, c = f λ, to solve problems involving speed, frequency and wavelength of light.
- Discuss the electromagnetic spectrum in terms of frequency and wavelength.
- Arrange the spectrum in order of increasing/decreasing frequency and wavelength.
- State uses of electromagnetic radiation.
- Describe a photon of light as a quantum of energy.
- Use the equation, E = hf, to do calculations involving energy, frequency and wavelength of light.
- 3.2 Paper 2
| Representing Chemical Change (Grade 10) (This section must be read in conjunction with the CAPS, p. 22.) |
Balanced chemical equations
- Represent reactions in equations balancing equations.
Intermolecular forces
Intermolecular and interatomic forces (chemical bonds)
- Name and explain the different intermolecular forces (Van der Waal's forces):
- Dipole-dipole forces: forces between two polar molecules
- Induced dipole forces or London forces: forces between non-polar molecules
- Hydrogen bonding: forces between molecules in which hydrogen is covalently bonded to nitrogen, oxygen or fluorine – a special case of dipole-dipole forces
- Describe the difference between intermolecular forces and interatomic forces using a diagram of a group of small molecules, and in words.
Example:
- State the relationship between intermolecular forces and molecular size. For non-polar molecules, the strength of induced dipole forces increases with molecular size.
- Explain the effect of intermolecular forces on boiling point, melting point and vapour pressure.
- Boiling point: The temperature at which the vapour pressure equals atmospheric pressure. The stronger the intermolecular forces, the higher the boiling point.
- Melting point: The temperature at which the solid and liquid phases of a substance are at equilibrium. The stronger the intermolecular forces, the higher the melting point.
- Vapour pressure: The pressure exerted by a vapour at equilibrium with its liquid in a closed system. The stronger the intermolecular forces, the lower the vapour pressure.
- Define viscosity as the resistance of a fluid (liquid or gas) to flow. The greater a fluid's viscosity, the more slowly is flows.
| Matter and Material: Organic Chemistry (This section must be read in conjunction with the CAPS, p. 46–47.) |
Molecular and structural functional groups, saturated and unsaturated structures, isomers
- Define organic molecules as molecules containing carbon atoms.
- Hydrocarbons are organic compounds containing only carbon atoms and hydrogen atoms.
- Write down molecular and structural formulae of organic compounds of up to six carbons for:
- Alkanes (no ring structures)
- Alkenes (no ring structures)
- Alkynes
- Alkyl halides (Haloalkanes) (primary, secondary and tertiary haloalkanes; no ring structures)
- Aldehydes
- Ketones
- Alcohols (primary, secondary and tertiary alcohols)
- Carboxylic acids
- Esters
Distinguish between:
- Different homologous series
- Saturated and unsaturated hydrocarbons
- Identify compounds up to six carbon atoms that are saturated, unsaturated and are structural isomers.
- Know the general formulae of different homologous series.
- Hydrocarbons are organic compounds that consist of hydrogen and carbon only.
- Saturated hydrocarbons contain only single covalent bonds between carbon atoms.
- Unsaturated compounds contain covalent double or triple bonds between the carbon atoms.
Define the following terms/concepts:
- Functional group: An atom or a group of atoms that determine the chemistry of a molecule OR an atom or a group of atoms that determine(s) the physical and chemical properties of a group of organic compounds.
- Homologous series: A series of organic compounds that can be described by the same general formula and where each member differs from the next by a CH2 group.
| Homologous series | Structure of functional group | |
| Structure | Name/Description | |
| Alkanes | | Only C-H and C-C single bonds |
| Alkenes | | Carbon-carbon double bond |
| Alkynes | | Carbon-carbon triple bond |
| Haloalkanes | 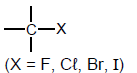 | - |
| Alcohols |  | Hydroxyl group bonded to a saturated C atom |
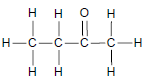
| Aldehydes | | Formyl group |
| Ketones | 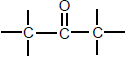 | Carbonyl group bonded to two C atoms |
| Carboxylic acids | | Carboxyl group |
| Esters | 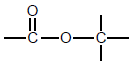 | - |
- Write structural formulae for given isomers and name them.
- A structural formula of a compound shows which atoms are attached to which within the molecule. Atoms are represented by their chemical symbols and lines are used to represent ALL the bonds that hold the atoms together.

- Structural isomers are organic molecules with the same molecular formula, but different structural formulae.
- Restrict structural isomers to chain isomers, positional isomers and functional isomers.
- Chain isomers have the same molecular formula, but different types of chains, e.g. butane and 2-methylpropane.

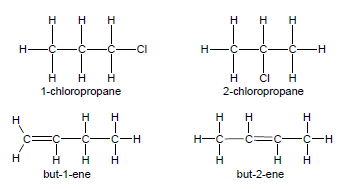
- Positional isomers have the same molecular formula, but different positions of the side chain, substituents or functional groups on the parent chain, e.g. 1-chloropropane and 2-chloropropane or but-2-ene and but-1-ene.
- Functional isomers have the same molecular formula, but different functional groups, e.g. methyl methanoate and ethanoic acid.

IUPAC naming and formulae
- Write down the IUPAC name when given the structural formula for alkanes, alkenes, alkynes, alkylhalides (haloalkanes), aldehydes, ketones, alcohols, carboxylic acids and esters, restricted to one functional group per compound, except for haloalkanes. For haloalkanes, a maximum two functional groups per molecule.
- Write down the structural formula when given the IUPAC name for alkanes, alkenes, alkynes, alkylhalides (haloalkanes), aldehydes, ketones, alcohols, carboxylic acids and esters.
- Identify alkyl substituents (methyl- and ethyl-) in a chain to a maximum of TWO alkyl substituents on the parent chain.
- When naming haloalkanes, the halogen atoms do not get preference over alkyl groups – numbering should start from the end nearest to the first substituent, either the alkyl group or the halogen. In haloalkanes, where e.g. a Br and a Cℓ have the same number when numbered from different ends of chain, Br gets alphabetical preference. When an alkyl group is a substituent in a molecule, it should be treated as a substituent.
- When writing IUPAC names, substituents appear as prefixes written alphabetically (bromo-, chloro-, ethyl-, methyl-), ignoring the prefixes di- and tri-.
Physical properties (boiling point, melting point, vapour pressure and viscosity), relationships
- Discuss relationships in physical properties of alkanes, alkenes, alkynes, alkylhalides (haloalkanes), aldehydes, ketones, alcohols, carboxylic acids and esters.
- Compare physical properties of different homologous series.
- For a given example (from the above functional groups), explain the relationship between physical properties and:
- Strength of intermolecular forces, i.e. hydrogen bonds, dipole-dipole forces, induced dipole forces
- Type of functional groups
- Chain length
- Branched chains
Reactions of organic compounds
Oxidation (combustion of hydrocarbons)
- Write down an equation for the combustion of hydrocarbons in excess oxygen.
Substitution and addition reactions
- Identify reactions as substitution or addition.
- Write down, using structural formulae, equations and reaction conditions for the following addition reactions of alkenes:
- Hydrohalogenation: The addition of a hydrogen halide to an alkene
- Halogenation: The reaction of a halogen (Br2, Cℓ2) with a compound
- Hydration: The addition of water to a compound
- Hydrogenation: The addition of hydrogen to an alkene
- Write down, using structural formulae, equations and reaction conditions for the following substitution reactions:
- Hydrolysis of haloalkanes
- Hydrolysis: The reaction of a compound with water
- Reactions of HX (X = Cℓ, Br) with alcohols to produce haloalkanes
- Halogenation of alkanes. The reaction of a halogen (Br2, Cℓ2) with a compound
Plastics and polymers (ONLY BASIC POLYMERISATION as application of organic chemistry)
Describe the following terms:
- Macromolecule: a molecule that consists of a large number of atoms.
- Polymer: a large molecule composed of smaller monomer units covalently bonded to each other in a repeating pattern
- Monomer: small organic molecules that can be covalently bonded to each other in a repeating pattern
- Polymerisation: a chemical reaction in which monomer molecules join to form a polymer
- Plastics: synthetic materials derived from organic compounds.
- Identify monomers from given addition polymers.
- Discuss the industrial uses of polythene.
| Matter and Materials (This section must be read in conjunction with the CAPS, p. 45.) |
Electronic properties of matter
- A semiconductor is a material that has electrical conductivity between that of a conductor and an insulator.
- Examples of semiconductors:
| Group | Element | Material |
| IV | carbon | diamond |
| IV | silicon | silico |
| IV | germanium | germanium |
| IV | grey tin, α -tin | grey tin, α -tin |
- An intrinsic semiconductor is a pure semiconductor. For example: diamond, Si, Ge and Sn.
- Doping is the process of adding impurities to intrinsic semiconductors.
- The elements of group 3 (e.g. boron and gallium) and 5 (e.g. phosphorus and arsenic) can be used for doping.
- Discuss the:
- n-type semiconductor
- p-type semiconductor
- Construction and working of a p-n junction diode
- Know the characteristics of the p-n junction diode.
| Chemical change (Grade 11)(This section must be read in conjunction with the CAPS, p. 39.) |
Oxidation and reduction
Know the following definitions/terms:
- Oxidation: the loss of electrons
- Reduction: the gain of electrons
- Oxidising agent: a substance that is reduced/gains electrons OR a substance that undergoes reduction
- Reducing agent: a substance that is oxidised/loses electrons OR a substance that undergoes oxidation
- Electrolysis: the decomposition of a substance when an electric current is passed through it OR the chemical process in which electrical energy is converted to chemical energy OR the use of electrical energy to produce a chemical change
- Cathode: the electrode where reduction takes place
- Anode: the electrode where oxidation takes place
Write down the following reactions:
- Oxidation half-reaction
- Reduction half-reaction
- The overall cell reaction by combining two half-reactions
Assigning oxidation numbers
- Know the rules for assigning oxidation numbers.
- Assign oxidation numbers to various molecules.
| Chemical Change (Grade 12) Electrochemical cells (This section must be read in conjunction with the CAPS, p. 55.) |
Electrolytic cells and galvanic cells
- Define the electrolytic cell as an electrochemical cell that converts electrical energy to chemical energy. It is a non-spontaneous.
- Define the galvanic (voltaic) cell as an electrochemical cell that converts chemical energy to electrical energy. It is spontaneous.
- Define an electrolyte as a solution/liquid/dissolved substance that conducts electricity through the movement of ions.
Understanding the processes and redox reactions taking place in electrolytic cells
- Describe the movement of ions in the solution.
- State the direction of electron flow in the external circuit.
- Write equations for the half-reactions taking place at the anode and cathode.
- Write down the overall cell reaction by combining two half-reactions.
- Describe, using half-reactions and the equation for the overall cell reaction as well as the layout of the particular cell using a schematic diagram, the following electrolytic process:
- The decomposition of copper (II) chloride
- Electroplating a metal by another metal
Understanding the processes and redox reactions taking place in galvanic cells
- Describe the movement of ions in the solutions and through the salt bridge.
- State the direction of electron flow in the external circuit.
- Write down the half-reactions that occur at the electrodes.
- State the function of the salt bridge.
- Name the components of a galvanic cell.
- State the functions of all components of a galvanic cell.
- Use cell notation or diagrams to represent a galvanic cell.
- When writing cell notation, the following convention should be used:
- Cell terminals (electrodes) are written on the outside of the cell notation.
- Active electrodes: reducing agent | oxidised species || oxidising agent | reduced species
- Predict the half-cell in which oxidation will take place when two half-cells are connected.
- Predict the half-cell in which reduction will take place when connected to another half-cell.
- Write down the overall cell reaction by combining two half-reactions.
- Use the Table of Standard Reduction Potentials to calculate the emf of a standard galvanic cell.
- Use a positive value of the standard emf as an indication that the reaction is spontaneous under standard conditions.
- Determine the electrode potential of a galvanic cell, e.g. Cu-Zn cell or any other galvanic cell.
Standard conditions
- Write down the standard conditions under which standard electrode potentials are determined.
Alternate Energies
Discuss the following alternate energies:
- Biodiesel
- Fuel cell
- Photovoltaic cell
- Discuss the use of alternate energies and their environmental impact.
4. GENERAL INFORMATION
4.1 Quantities, symbols and units
The most common quantities, symbols and SI units used in introductory Technical Sciences are listed below. A quantity should not be confused with the unit in which it is measured.
| Quantity | Preferred symbol | Alternative symbol | Unit name | Unit symbol |
| mass | m | kilogram | kg | |
| position | x,y | metre | m | |
| displacement | Δx, Δy | s | metre | m |
| velocity | vx, vy | u,v | metre per second | m·s-1 |
| initial velocity | vi | u | metre per second | m·s-1 |
| final velocity | vf | v | metre per second | m·s-1 |
| acceleration | a | metre per second per second | m·s-2 | |
| acceleration due to gravity | g | metre per second per second | m·s-2 | |
| time (instant) | t | second | s | |
| time interval | Δt | second | s | |
| energy | E | joule | J | |
| kinetic energy | K | Ek | joule | J |
| potential energy | U | Ep | joule | J |
| work | W | joule | J | |
| work function | W0 | joule | J | |
| power | P | watt | W | |
| momentum | p | kilogram metre per second | kg·m·s-1 | |
| force | F | newton | N | |
| weight | w | Fg | newton | N |
| normal force | N | FN | newton | N |
| tension | T | FT | newton | N |
| friction force | f | Ff | newton | N |
| coefficient of friction | μ,μs,μk | (none) | ||
| torque | τ | newton metre | N.m | |
| wavelength | λ | metre | m | |
| frequency | f | v | hertz per second | Hz or s-1 |
| period | T | second | s | |
| speed of light | c | metre per second | m·s-1 | |
| refractive index | n | (none) | ||
| focal length | f | metre | m | |
| object distance | s | u | metre | m |
| image distance | s' | v | metre | m |
| magnification | m | (none) | ||
| charge | Q,q | coulomb | C | |
| electric field | E | newton per coulomb or volt per metre | N·C-1 or V·m-1 | |
| electric potential at point P | VP | volt | V | |
| potential difference | ΔV, V | volt | V | |
| emf | E | ε | volt | V |
| current | I, i | ampere | A | |
| resistance | R | ohm | Ω | |
| internal resistance | r | ohm | Ω | |
| magnetic field | B | tesla | T | |
| magnetic flux | Φ | tesla.metre2 or weber | T·m2 or Wb |
Conventions (e.g. signs, symbols, terminology and nomenclature)
The syllabus and question papers will conform to generally accepted international practices.
NOTE:
- For marking purposes, alternative symbols will also be accepted.
- Separate compound units with a multiplication dot, not a full stop, e.g. m·s-1.
For marking purposes, m.s-1will also be accepted. - Use the equal sign only when it is mathematically correct, e.g.
Incorrect: 1 cm = 1 m (on a scale drawing)
Correct: 1 cm = 10-2 m 1 cm represents 1 m (on a scale drawing)
4.2 Information sheets – Paper 1
TABLE 1: PHYSICAL CONSTANTS
| NAME | SYMBOL | VALUE |
| Acceleration due to gravity | g | 9,8 m·s-2 |
| Speed of light in a vacuum | c | 3,0 x 108 m·s-1 |
| Planck's constant | h | 6,63 x 10-34 J·s |
| Permittivity of free space | εº | 8,85 x 10 -12 F·m-1 |
TABLE 2: FORMULAE
FORCE
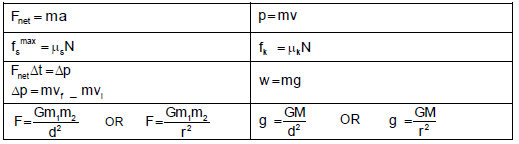
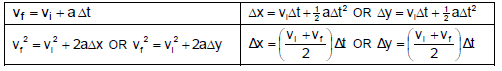
WORK, ENERGY AND POWER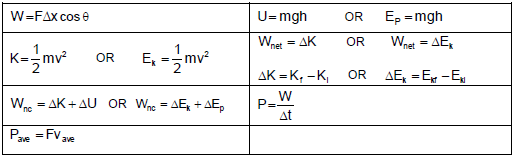
ELASTICITY, VELOCITY AND HYDRAULICS
| σ = F A | ε = Δl L |
| σ = K ε | F1 = F2 A1 A2 |
ELECTROSTATICS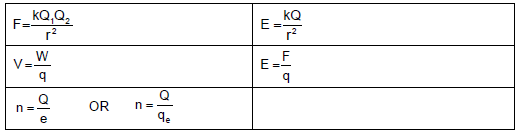
CURRENT ELECTRICITY
ELECTROMAGNETISM
WAVES, SOUND AND LIGHT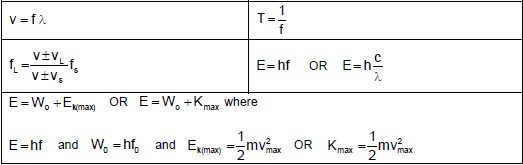
4.3 Information Sheets – Paper 2
TABLE 1: PHYSICAL CONSTANTS
| NAME | SYMBOL | VALUE |
| Standard pressure | pθ | 1,013 x 105 Pa |
| Standard temperature | Tθ | 0ºC/ 273 K |
TABLE 2 ; FORMULAE
TABLE 3 ; THE PERODIC TABLE OF ELEMENTS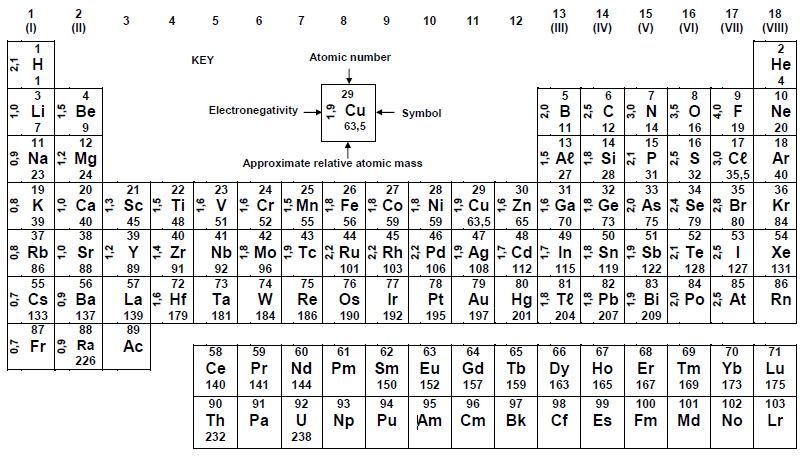
TABLE 4A: STANDARD REDUCTION POTENTIALS
TABLE 4B: STANDARD REDUCTION POTENTIALS

4.4 Assessment taxonomy for Technical Sciences
The following table provides a possible hierarchy of cognitive levels that must be used to ensure tasks include opportunities for learners to achieve at various levels and tools for assessing the learners at various levels. The verbs given in the fifth column below could be useful when formulating questions associated with the cognitive levels given in the first column.
| DESCRIPTION OF COGNITIVE LEVEL | LEVEL | EXPLANATION | SKILLS DEMONSTRATED | ACTION VERBS |
| CREATING | 4 | The learner creates new ideas and information using the knowledge previously learned or at hand. At the extended abstract level, the learner makes connections not only within the given subject area but also beyond it and generalises and transfers the principles and ideas underlying the specific instance. The learner works with relationships and abstract ideas. |
| Devise, predict, invent, propose, construct, generate, make, develop, formulate, improve, plan, design, produce, forecast, compile, originate, imagine |
| EVALUATING | The learner makes decisions based on in-depth reflection, criticism, and assessment. The learner works at the extended abstract level. |
| Combine, integrate, modify, rearrange, substitute, compare, prepare, generalise, rewrite, categorise, combine, compile, reconstruct, organise, justify, argue, prioritise, judge, rate, validate, reject, appraise, judge, rank, decide, criticise | |
| ANALYSING | 3 | The learner appreciates the significance of the parts in relation to the whole. Various aspects of the knowledge become integrated, the learner shows a deeper understanding and the ability to break down a whole into its component parts. Elements embedded in a whole are identified and the relations among the elements are recognised. |
| Analyse, separate, order, explain, connect, classify, arrange, divide, compare, select, infer, break down, contrast, distinguish, draw, illustrate, identify, outline, point out, relate, question, appraise, argue, defend, debate, criticise, probe, examine, investigate, experiment |
| APPLYING | The learner has the ability to use (or apply) knowledge and skills in other familiar situations and new situations. |
| Apply, demonstrate, calculate, complete, illustrate, show, solve, examine, modify, relate, change, classify, experiment, discover, construct, manipulate, prepare, produce, draw, make, compile, compute, sequence, interpret | |
| UNDERSTANDING | 2 | The learner grasps the meaning of information by interpreting and translating what has been learned. |
| Summarise, describe, interpret, calculate, contrast, associate, distinguish, estimate, differentiate, discuss, extend, comprehend, convert, explain, give example, rewrite, infer, review, observe, give main idea |
| REMEMBERING | 1 | The learner is able to recall, remember and restate facts and other learned information. |
| List, define, tell, describe, identify, show, know, label, collect, select, reproduce, match, recognise, examine, quote, name |
5. MARKING GUIDELINES: PAPER 1
5.1 Calculations
5.1.1 Marks will be awarded for: correct formula, correct substitution, correct answer with unit
5.1.2 No marks will be awarded if an incorrect or inappropriate formula is used, even though there may be relevant symbols and applicable substitutions.
5.1.3 When an error is made during substitution into a correct formula, a mark will be awarded for the correct formula and for the correct substitutions, but no further marks will be given.
5.1.4 If no formula is given, but all substitutions are correct, the candidate will forfeit one mark.
5.1.5 No penalisation if zero substitutions are omitted in calculations where correct formula/principle is given correctly.
5.1.6 Mathematical manipulations and change of subject of appropriate formulae carry no marks, but if a candidate starts off with the correct formula and then changes the subject of the formula incorrectly, marks will be awarded for the formula and the correct substitutions. The mark for the incorrect numerical answer is forfeited.
5.1.7 Marks are only awarded for a formula if a calculation has been attempted, i.e. substitutions have been made or a numerical answer given.
5.1.8 Marks can only be allocated for substitutions when values are substituted into formulae and not when listed before a calculation starts.
5.1.9 Final answers to all calculations, when not specified in the question, must be rounded off to a minimum of TWO decimal places.
5.1.10 If a final answer to a calculation is correct, full marks will not automatically be awarded. Markers will always ensure that the correct/appropriate formula is used and that workings, including substitutions, are correct.
5.1.11 Questions in which a series of calculations have to be made (e.g. a circuit-diagram question) do not necessarily always have to follow the same order. FULL MARKS will be awarded, provided it is a valid solution to the problem. However, any calculation that will not bring the candidate closer to the answer than the original data, will not count any marks.
5.2 Units
5.2.1 Candidates will only be penalised once for the repeated use of an incorrect unit within a question.
5.2.2 Units are only required in the final answer to a calculation.
5.2.3 Marks are only awarded for an answer, and not for a unit per se. Candidates will therefore forfeit the mark allocated for the answer in each of the following situations:
- Correct answer + wrong unit
- Wrong answer + correct unit
- Correct answer + no unit
5.2.4 SI units must be used, except in certain cases, e.g. V∙m-1 instead of N∙C-1, and cm∙s-1 or km∙h-1 instead of m∙s-1 where the question warrants this.
5.3 General
5.3.1 If one answer or calculation is required, but two are given by the candidate, only the first one will be marked, irrespective of which one is correct. If two answers are required, only the first two will be marked, etc.
5.3.2 For marking purposes, alternative symbols (s, u, t, etc.) will also be accepted.
5.3.3 Separate compound units with a multiplication dot, not a full stop, e.g. m·s-1. For marking purposes, m.s-1 and m/s will also be accepted.
5.4 Positive marking
Positive marking regarding calculations will be followed in the following cases:
5.4.1 Subquestion to subquestion: When a certain variable is incorrectly calculated in one subquestion (e.g. 3.1) and needs to be substituted into another subquestion (3.2 or 3.3), full marks are to be awarded for the subsequent subquestions.
5.4.2 A multistep question in a subquestion: If the candidate has to calculate, for example, current in the first step and gets it wrong due to a substitution error, the mark for the substitution and the final answer will be forfeited.
5.5 Negative marking
Normally an incorrect answer cannot be correctly motivated if based on a conceptual mistake. If the candidate is therefore required to motivate in QUESTION 3.2 the answer given to QUESTION 3.1, and QUESTION 3.1 is incorrect, no marks can be awarded for QUESTION 3.2. However, if the answer to, for example, QUESTION 3.1 is based on a calculation, the motivation for the incorrect answer in QUESTION 3.2 should be considered.
6. MARKING GUIDELINES: PAPER 2
6.1 Calculations
6.1.1 Marks will be awarded for: correct formula, correct substitution, correct answer with unit
6.1.2 No marks will be awarded if an incorrect or inappropriate formula is used, even though there may be relevant symbols and applicable substitutions.
6.1.3 When an error is made during substitution into a correct formula, a mark will be awarded for the correct formula and for the correct substitutions, but no further marks will be given.
6.1.4 If no formula is given, but all substitutions are correct, the candidate will forfeit one mark.
6.1.5 Marks are only awarded for a formula if a calculation has been attempted, i.e. substitutions have been made or a numerical answer has been given.
6.1.6 Marks can only be allocated for substitutions when values are substituted into formulae and not when listed before a calculation starts.
6.1.7 The final answer to all calculations, when not specified in the question, must be rounded off to a minimum of TWO decimal places.
6.1.8 If a final answer to a calculation is correct, full marks will not automatically be awarded. Markers will always ensure that the correct/appropriate formula is used and that workings, including substitutions, are correct.
6.1.9 Mathematical manipulations and change of the subject of appropriate formulae carry no marks, but if a candidate starts off with the correct formula and then changes the subject of the formula incorrectly, marks will be awarded for the formula and the correct substitutions. The mark for the incorrect numerical answer is forfeited.
6.2 Units
6.2.1 Candidates will only be penalised once for the repeated use of an incorrect unit within a question.
6.2.2 Units are only required in the final answer to a calculation.
6.2.3 Marks are only awarded for an answer and not for a unit per se. Candidates will therefore forfeit the mark allocated for the answer in each of the following situations:
- Correct answer + wrong unit
- Wrong answer + correct unit
- Correct answer + no unit
6.2.4 Separate compound units with a multiplication dot, not a full stop, e.g. mol·dm-3. Accept mol.dm-3 (or mol/dm3) for marking purposes.
6.3 General
6.3.1 If one answer or calculation is required, but two are given by the candidate, only the first one will be marked, irrespective of which one is correct. If two answers are required, only the first two will be marked, etc.
6.3.2 When a chemical FORMULA is asked, and the NAME is given as answer, the candidate forfeits the marks. The same rule applies when the NAME is asked, and the FORMULA is given.
6.3.3 When redox half-reactions are to be written, the correct arrow should be used. If the equation
H2S → S + 2H+ + 2e- (2)
2
is the correct answer, the marks must be given as follows:
H2S S + 2H+ + 2e- (1)
2
H2S ← S + 2H+ + 2e- (0)
2
S + 2H+ + 2e- ← H2S (2)
2
S + 2H+ + 2e- ← H2S (0)
2
6.3.4 When candidates are required to give an explanation involving the relative strength of oxidising and reducing agents, the following will not be accepted:
- Stating the position of a substance on Table 4 only (e.g. Cu is above Mg).
- Using relative reactivity only (e.g. Mg is more reactive than Cu).
- The correct answer would be for instance: Mg is a stronger reducing agent than Cu, and therefore Mg will be able to reduce Cu2+ ions to Cu. The answer can also be given in terms of the relative strength as electron acceptors and donors.
6.3.5 One mark is forfeited when the charge of an ion is omitted per equation (not for the charge on an electron).
6.3.6 The error-carrying principle does not apply to chemical equations or half-reactions. For example, if a learner writes the wrong oxidation/reduction half-reaction in the subquestion and carries the answer to another subquestion (balancing of equations or calculation of (Eθcell), then the learner will not be credited for this substitution.
6.3.7 In the structural formula of an organic molecule all hydrogen atoms must be shown. Marks must be deducted if hydrogen atoms are omitted.
6.3.8 When a structural formula is required, marks must be deducted if the candidate writes the condensed formula.
6.3.9 When a IUPAC name is asked and the candidate omits the hyphen (e.g. instead of pent-1-ene or 1-pentene the candidate writes pent 1 ene or 1 pentene), marks will be forfeited.
6.3.10 When a chemical reaction is asked, marks are awarded for correct reactants, correct products and correct balancing.
If only a reactant(s) followed by an arrow, or only a product(s) preceded by an arrow, is/are written, marks may be awarded for the reactant(s) or product(s). If only a reactant(s) or only a product(s) is/are written, without an arrow, no marks are awarded for the reactant(s) or product(s).
Examples:
N2 + 3H2 → 2NH3 bal 3
3
N2 + H2 → 1
3
→ NH3 1
3
N2 + H2 0
3
NH3 0
3
6.4 Positive marking
Positive marking regarding calculations will be followed in the following cases: 6.4.1 Subquestion to subquestion: When a certain variable is calculated in one subquestion
(e.g. QUESTION 3.1) and needs to be substituted in another (QUESTION 3.2 or QUESTION 3.3), e.g. if the answer for QUESTION 3.1 is incorrect and is substituted correctly in QUESTION 3.2 or QUESTION 3.3, full marks are to be awarded for the subsequent subquestions.
6.4.2 A multistep question in a subquestion: If the candidate has to calculate, for example, the current in the first step and gets it wrong due to a substitution error, the mark for the substitution and the final answer will be forfeited.
6.5 Negative marking
Normally an incorrect answer cannot be correctly motivated if based on a conceptual mistake. If the candidate is therefore required to motivate in QUESTION 3.2 the answer given to QUESTION 3.1, and QUESTION 3.1 is incorrect, no marks can be awarded for QUESTION 3.2. However, if the answer for, for example, QUESTION 3.1 is based on a calculation, the motivation for the incorrect answer in QUESTION 3.2 could be considered.
7. CONCLUSION
This Examination Guidelines document is meant to articulate the assessment aspirations espoused in the CAPS document. It is therefore not a substitute for the CAPS document, which teachers should teach to.
Qualitative curriculum coverage as enunciated in the CAPS cannot be over-emphasised.