GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS FEBRUARY/MARCH 2017
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupGRADE 12 MATHEMATICS
PAPER 2
NSC PAST PAPERS AND MEMOS
FEBRUARY/MARCH 2017
NOTE:
- If a candidate answered a question TWICE, mark only the FIRST attempt.
- If a candidate has crossed out an attempt to answer a question and did not redo it, mark the crossed-out version.
- Consistent accuracy applies in ALL aspects of the marking memorandum. Stop marking at the second calculation error.
- Assuming answers/values in order to solve a problem is NOT acceptable.
MEMORANDUM
QUESTION 1
Ogive 
An incomplete frequency table is also given for the data.
| Amount of money (in R) | 10 ≤ x < 20 | 20 ≤ x < 30 | 30 ≤ x < 40 | 40 ≤ x < 50 | 50 ≤ x < 60 |
| Frequency | a | 13 | 20 | b | 4 |
1.1 | 65 learners | ✔ answer (1) |
1.2 | Modal class: 30 ≤ x < 40 | ✔ answer (1) |
1.3 | a = 12 | ✔ answer |
1.4 | No. of learners = 65 – 54 OR 65 – 55 | ✔ 54 or 55 [6] |
QUESTION 2
2.1 
2.1.1 | IQR of Class B/IKV van Klas B = Q3 − Q1 = 72 – 51 = 21 marks/punte | ✔72 and 51 |
2.1.2 | Although the boxes contain the same number of data points, the marks for Class A are more widely spread | ✔✔ Class A is more widely spread (2) |
2.1.3 | Medians are the same | ✔✔any TWO of the 3 reasons mentioned (2) |
2.2
COUPLE | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
JUDGE 1 | 18 | 4 | 6 | 8 | 5 | 12 | 10 | 14 |
JUDGE 2 | 15 | 6 | 3 | 5 | 5 | 14 | 8 | 15 |
2.2.1 | a = –0,03 | ✔ value a |
2.2.2 | yˆ= –0,03 + 0,93(15) | ✔ substitution |
2.2.3 | Yes OR they are consistent, because r = 0,9. (r = 0,89567…) | ✔ statement [13] |
QUESTION 3 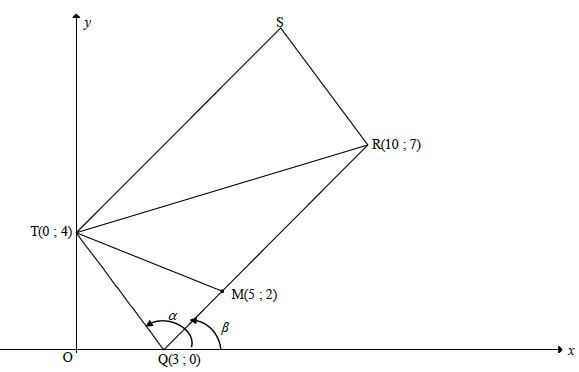
3.1 | mTQ = 4 - 0 | ✔ answer (1) |
3.2 | d = √(x2 - x1)2 + (y2 - y1)2 | ✔substitution |
3.3 | mFQ = mTQ 4k −12 = 24 | ✔ equating gradient
✔ gradient |
| 3.4 | Using transformation: | ✔✔ x–value
|
| 3.5 | TSR = TQR [opp∠ s of ΙΙ] OR TQ = SR = 5 | ✔TQR = α −β ✔ tanα = mTQ ✔ α ✔ tan β = mRQ
✔ length of TQ OR SR |
| 3.6.1 | MQ = √(5 - 3)2 + (2 - 0)2 MQ = √8 MQ = √8 RQ √98 =2/7 OR 0,29 Answer only; full marks | ✔substitution |
| 3.6.2 | area of ΔTQM = ½.QM. ⊥h [⊥h same] OR area of ΔTQM = QM OR area of ΔTQM = ½.QM. ⊥h OR area of ΔTQM = ½.QT.QM. sin(α - β) | ✔ area of ΔTQM = 2
✔ ½.QM. ⊥h [23] |
QUESTION 4 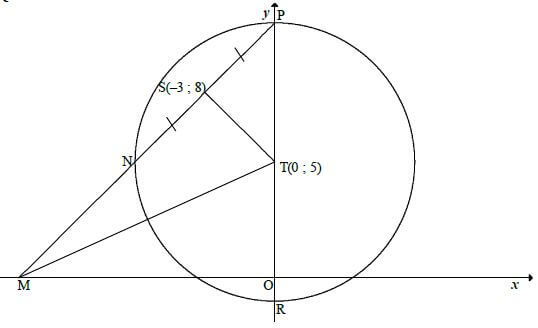
QUESTION 6
4.1 | line from centre to midpt of chord | ✔ answer (1) |
4.2 | mST = 8 - 5 | ✔ subst (–3 ; 8) and (0 ; 5) into gradient formula |
4.3 | P(0 ; 11) [y-intercept of chord NP] | ✔ coordinates of P |
4.4 | M(–11 ; 0) [x–intercept of NP] | ✔✔ coordinates of M |
| 4.5 | MT = diameter [conv ∠ in ½ circle] radius = √146 units 2 Centre of circle = midpoint MT =[ -11 ; 5] [ 2 2 ] Equation of circle through S, T and M: =[ x + -11 ]2 + [ x - 5 ]2 = 146 [ 2 ] [ 2] 4 OR =[ x + 5½ ]2 + [ x - 2½]2 = 73 2 =6,04 | ✔ radius of circle |
| [19] | ||
| QUESTION 5 | ||
| 5.1 | a = −1 | ✔ answer |
| 5.2 | f(3x)= – sin 3x | ✔360º |
| 5.3 | x ∈ [90º ; 135º) ∪ {180º} | ✔ 90º and 135º in interval form |
| [7] | ||
| QUESTION 6 | ||
| 6.1.1 | sin (360º – 36º) = – sin 36º | ✔ answer (1) |
| 6.1.2 | cos 72º = cos(2×36º) | ✔ double angle |
| 6.2 | R.T.P.: 1 - tan2θ = cos2θ OR LHS = 1 + tan2θ - tan2θ OR LHS = 1 - [sin2θ ÷ (1 + sin2θ)] | ✔writing as a single fraction
✔writing as a single fraction
✔ quotient identity |
| 6.3 | cos2½x = ¼ OR | ✔✔ cos2½x = ¼ |
| 6.4.1 | sin(A −B)= cos[90º − (A − B)] OR sin(A −B)= cos[90º − (A − B)] | ✔ co–ratio
|
| 6.4.2 | sin(x + 64º)cos(x + 379º) + sin(x + 19º)cos(x + 244º) = sin(x + 64º)cos(x + 19º) + sin(x + 19º)[-cos(x + 64º)] = sin(x + 64º)cos(x + 19º) - cos(x + 64º)sin(x + 19º) = sin[x + 64º - (x + 19º)] = sin 45º = 1 √2 | ✔cos(x + 379º) = cos(x +19º) |
| [23] | ||
QUESTION 7
7.1 | sin 27º = CD | ✔ substitution in correct trig ratio |
7.2 | cos 40º = 10 | ✔substitution in correct trig ratio |
7.3 | AC2 = CE2 + AE2 - 2CE.AE(cos AEC) | ✔ correct use of cosine rule in ΔACE
|
| [8] |
QUESTION 8 
8.1 | ˆQ = 72° [opp ∠s of cyclic quad] | ✔ S |
8.2 | R2 = P1 [∠s opp equal sides] | ✔ S/R |
8.3 | P2 = 42° | ✔ S |
8.4 | R3 = P1 + P2 OR R1 =180° −108° − 42° = 30° | ✔ R ✔ R1 = 30°
|
| [8] |
QUESTION 9 
9.1.1 | ST = SW [prop theorem ; TW || QP] | ✔ S |
9.1.2 | SV = SW | ✔ answer (1) |
9.2 | ST= SV [both equal WS /PW ] | ✔ S |
9.3 | ΔVWS ||| ΔRPS | ✔ ΔRPS (any order) (1) |
9.4 | WV = SW [ ΔVWS ||| Δ RPS] OR WV = SV [ ΔVWS ||| Δ RPS] | ✔ ratio |
| [10] |
QUESTION 10
10.1 
| 10.1 | Constr : | ✔ construction |
10.2 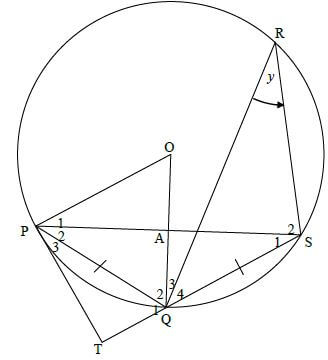
10.2.1 | ∠s in the same segment | ✔ R (1) |
10.2.2 | P2 = S1 = y [∠s opp equal sides] | ✔ S ✔ R |
10.2.3 | POQ = 2S1 = 2y | ✔ S ✔ R (2) |
10.2.4 | TPA = P2 + P3 = 2y [proved in 11.2.2] | ✔TPA = POQ |
| 10.2.5 | OPQ + OQP = 180º - 2y [sum of∠ s/e in Δ] OR OTP = 90º [radius ⊥ tangent] OR POSQ is a kite OR In ΔOAP and ΔOAS | ✔ S ✔ S ✔ R ✔✔✔ S ✔ S |
| [19] |
QUESTION 11 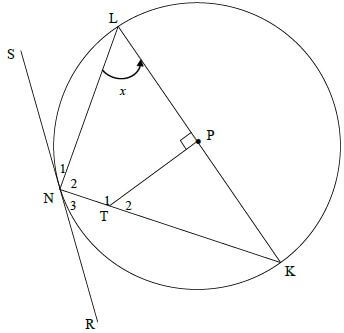
11.1 | N2 = 90° [∠ in semi-circle] OR N2 = 90° [∠ in semi-circle] | ✔ S ✔ R ✔ S ✔ R |
11.2 | T2 = PLN = x [ext ∠ of cyclic quad] OR K = 90° − x [sum of ∠s/e in ∆] OR N3 = x [tan chord theorem] | ✔ R ✔ R ✔ R |
| 11.3.1 | In ΔKTP and ΔKLN: OR In ΔKTP and ΔKLN: | ✔ S ✔ S |
| 11.3.2 | KT= KP [||| Δs] | ✔ S/R |
| [14] | ||
| TOTAL | [150] | |