GRADE 12 MATHEMATICS
PAPER 1 
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017

INSTRUCTIONS AND INFORMATION 
Read the following instructions carefully before answering the questions.

1. This question paper consists of ELEVEN questions. Answer ALL the questions.
2. Clearly show ALL calculations, diagrams, graphs, et cetera that you have used in  determining your answer. 
3. You may use an approved scientific calculator (non-programmable and non graphical), unless stated otherwise. 
4. Answers only will not necessarily be awarded full marks.
5. If necessary, round off answers to TWO decimal places, unless stated otherwise.
6. Diagrams are NOT necessarily drawn to scale.
7. Number the answers correctly according to the numbering system used in this  question paper. 
8. Write neatly and legibly.
9. An information sheet with formulae is included at the end of the question paper.

QUESTIONS

QUESTION 1 
Solve for x: 
1.1 2x(x+ 1) − 7(x + 1) = 0 (3)
1.2 x² − 5x − 1 = 0 , correct to two decimal places. (3)
1.3 4x² + 1 ≥ 5x (4)
1.4 5^4x+3_. 100^−2x+1 = 50 000 (4)
1.5 Solve for x and y simultaneously. 
x = 2y and x² + 2x − y − y² = 36 (5) 
1.6 Show that the roots of x² − kx + k − 1 = 0 are real and rational for all real  values of k. (4)

[23] 

QUESTION 2 
2.1 Given the following linear series: 3 + 7 + 11 + … … … + 483

2.1.1 How many terms does the above series have? (3)
2.1.2 Write the above series in sigma notation. (2) 

2.2 2t − 4 ; t − 3 ; 8 − 2t are the 10th , 11th and 12th terms of an arithmetic  sequence. 

2.2.1 Determine the value of t . (3)
2.2.2 Calculate the value of the first term. (3) 

2.3 The following information of a geometric pattern is given:  

T₁ + T₂ = −1 and T₃ + T₄ = −4 
Determine the numerical values of the first three terms if r > 0. (6)

[17]

QUESTION 3 
Given the following list of numbers in a quadratic sequence:  
41 ; 43 ; 47 ; 53 ; 61 ; 71 ; 83 ; 97 ; 113 ; 131 
3.1 Determine the general term of the above sequence if it has a constant second  difference. (5) 
3.2 Calculate T₄₁ and show that it is not a prime number. (3) 
3.3 Determine the unit digit of the 49 999 998^th term of the above sequence. (3)

[11] 

QUESTION 4 

4.1 Wayde invest R500 000 at 7,2% per annum compounded monthly. 

4.1.1 Write down an expression for the value of his investment after n full  years. (2) 
4.1.2 Determine the value of his investment after 5 full years. (2) 
4.1.3 If the investment exceeds R1 million rand after nfull years, calculate  the value of n . (3) 

4.2 Mr Jones wants to purchase a new car. The car cost R350 000 and he wants to  pay R10 000 per month for three years. The interest rate on a financed loan,  payable monthly, is 15% p.a. compounded monthly. 

4.2.1 Calculate how much he will have to give as a deposit, to the auto dealer. (5) 
4.2.2 Calculate his monthly payment if he pays no deposit and the car is  financed over 5 years, at an interest rate of 18,5% p.a. compounded  monthly. (4)

[16]

QUESTION 5 
The sketch shows the graph of f(x) = x(x + 3) and g(x) = −½x + 2.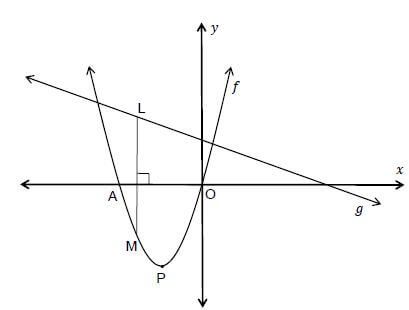 

5.1 Determine the coordinates of A. (1)
5.2 Calculate the coordinates of P, the turning point of f . (3)
5.3 Determine the average gradient of f between x = −5 and x = −3 . (3)
5.4 Determine the value(s) of x for which f(x) > 0. (2)
5.5 Determine the coordinates of the turning point of ℎ if ℎ(x) = f(x − 2). (2) 
5.6 L is a point on the straight line and M is a point on the parabola. LM is  perpendicular to the x-axis. Show that the length LM can be written as:  
LM =  - [x + ⁷/₄]²   + ⁸¹/₁₆    (4)

[15] 

QUESTION 6 
Given: ℎ(x) = 2^−x 

6.1 Draw a neat sketch of ℎ . (3) 
6.2 Determine the equation of q, the graph obtained by reflecting ℎ in the line  y = 0 . (1) 
6.3 Write down the equation of ℎ⁻¹, the inverse of ℎ, in the form y = … (2)
6.4 Write down the range of ℎ . (1)
6.5 Sketch the graph of ℎ−1 on the same set of axes as ℎ . (2) 
6.6 Determine the x-value(s) for which ℎ⁻¹(x) ≥ −3 . (2)

[11] 

QUESTION 7 
A sketch of the hyperbola f(x ) =  d - f
                                                     x - p ,  where p and d are constants, is given below.  
The dotted lines are the asymptotes. The point A(5; 0) is given on the graph of f.  

7.1 Determine the values of d and p . (2)
7.2 Show that the equation can be written as  y =         3        - 1
                                                                                  x - 2                               (2)
7.3 Write down the image of A if A is reflected about the axis of symmetry  y = x − 3. (2)

[6] 

QUESTION 8 
8.1 Given: f(x) = −2x² + p
Determine f′(x) from first principles. (5) 
8.2 Determine:    (4)

[9] 

QUESTION 9 
Given: f(x) = (x − 1)²(x + 3) 
9.1 Determine the turning points of f. (5) 
9.2 Draw a neat sketch of f showing all intercepts with the axes as well as the  turning points. (4) 
9.3 Determine the coordinates of the point where the concavity of f changes. (3)
9.4 Determine the value(s) of k, for which f(x) = k has three distinct roots. (2) 
9.5 Determine the equation of the tangent to f that is parallel to the line y = −5x if x < 0 . (6)

[20] 

QUESTION 10 
A closed rectangular box, with a rectangle as base, has a length (2x) cm and width  (x) cm. The total surface area (all 6 sides) is 243 cm^2. 
10.1 Show that the height, ℎ , is equal to [ 81 - 2x] cm
                                                                 [ 2x    3 ]
10.2 Show that the volume of the box, in terms of x , is given by the formula: 
V = 81x − ⁴/₃x³     (2) 
10.3 Calculate the value of x if the volume of the box is a maximum. (3) 

[7]

QUESTION 11 
11.1 You have to select a new password for your “Dropbox” account on your  computer. The password must consist of 3 digits and 2 letters of the alphabet in  that order. The digit 0(zero) is not allowed and no consonants are allowed. Any  digit may be repeated but the vowels may not be repeated. How many different  passwords are possible? (3) 
11.2 Using the letters in the word FUNDAMENTALS , determine: 

11.2.1 The number of unique 12 letter arrangements that can be formed (3) 
11.2.2 The probability that a new arrangement will start and end with the  letter N (3) 
11.3 In a city where the ratio of male to female is 1 : 2, one person is selected to flip a fair coin for the kick-off of a soccer tournament. 
11.3.1 Draw a tree diagram to show all possible outcomes of the coin toss. (3) 11.3.2 Determine the probability that it will be a woman who flips the coin. (1) 
11.3.3 Determine the probability that it will be a man who flips a head. (2)

[15] 
TOTAL: 150