GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS SEPTEMBER 2017
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupGRADE 12 MATHEMATICS
PAPER 2
NSC PAST PAPERS AND MEMOS
SEPTEMBER 2017
INSTRUCTIONS AND INFORMATION
- This question paper consists of 10 questions.
- Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
- Clearly show ALL calculations, diagrams graphs, et cetera which you have used in determining the answers.
- Answers only will NOT necessarily be awarded full marks.
- If necessary, round off your answers to TWO decimal places, unless stated otherwise
- Diagrams are not necessarily drawn to scale.
- You may use an approved scientific calculator (non-programmable and non-graphical) unless stated otherwise.
- An information sheet with formulae is included at the end of the question paper. 9. Write neatly and legibly.
QUESTIONS
QUESTION 1
A training company wants to know if there is a link between the hours spent in training by a particular category of employee and their productivity (units produced per day). The following data was extracted from files of 10 employees.
Employee | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Hours in training | 16 | 36 | 20 | 38 | 40 | 30 | 35 | 22 | 40 | 24 |
Productivity (units produced per day) | 45 | 70 | 44 | 56 | 60 | 48 | 75 | 60 | 63 | 38 |
1.1 Draw a scatter plot of the data on the grid provided in the ANSWER BOOK. (3)
1.2 Determine the equation of the least squares regression line. (3)
1.3 Draw the least squares regression line on the scatter plot drawn in QUESTION 1.1. (2)
1.4 Use the least squares regression line to predict the productivity (units produced per day), if a particular category of employee spent 25 hours in training. (2)
1.5 Determine the correlation coefficient of the data. (1)
1.6 Comment on the strength of relationship between the hours spent in training and the number of units produced per day. (1)
[12]
QUESTION 2
The marks obtained by learners of a certain school in a Mathematics test is represented in the histogram below: 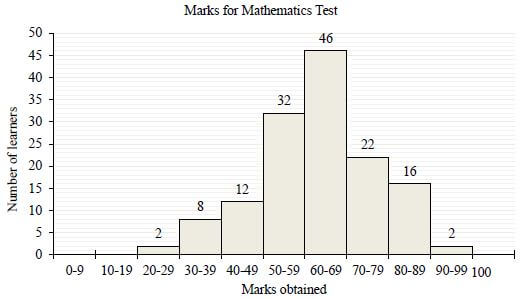
2.1 How many learners wrote the test? (1)
2.2 Write down the modal class. (1)
2.3 Draw the ogive for the given information. (4)
2.4 Use the ogive to estimate the interquartile range. (2)
[8]
QUESTION 3
In the diagram below, A (-1 ; 5), B (2 ; 6), C and D are the vertices of parallelogram ABCD. Vertex D lies on the x-axis. The equation of BC is x + 2y = 14. 
3.1 Determine the equation of line AD in the formy = mx + c. (3)
3.2 Determine the coordinates of D. (2)
3.3 If the coordinates of F are (10 ; 2), show that DF is perpendicular to BC. (3)
3.4 Calculate the length of AD. (Leave your answer in surd form.) (2)
3.5 Hence, or otherwise, calculate the area of parallelogram ABCD. (4)
3.6 Calculate the size of AB̂C. (6)
[20]
QUESTION 4
In the diagram below, the circle with centre S, passes through the origin, O, and intersects the x-axis at R and y-axis at T. The tangent to the circle at P(4 ; -6) intersects the x-axis at Q and the y-axis at U. 
4.1 Calculate the coordinates of S, the centre of the circle. (2)
4.2 Calculate the length of the radius of the circle. (Leave your answer in surd form.) (2)
4.3 Determine the equation of the circle in the form of (x − a)2 + (y − b)2 = r2. (2)
4.4 Why is QP̂U = 90°? (1)
4.5 Show that the equation of the tangent UQ is: y =2/3x −26/3. (4)
4.6 Determine the coordinates of T. (4)
4.7 Determine the ratio of Area △OTP in its simplest form. (5)
Area △PTU
[20]
QUESTION 5
5.1 Given: sin 2x =√15 and 0° ≤ 2x ≤ 90°.
x
Determine with the aid of a diagram and without using a calculator the value of cos x. (5)
5.2 Simplify the following expression to one trigonometric ratio of θ:
sin(180° − θ) . sin(540° − θ). cos(θ − 90°)
tan(−θ). sin2(360° − θ) (7)
5.3 Given the identity: sin 5x.cos 3x.−cos 5x .sin3x − 1 = −2 sin2x.
tan 2x
5.3.1 Prove the above identity. (4)
5.3.2 For which value(s) of x will the above identity be undefined for 0° ≤ x ≤ 180°. (4)
[20]
QUESTION 6
Given f(x) = tan 1/2x and g(x) = sin(x − 30°) for x ∈ [−90°; 180°]
6.1 On the same set of axes draw the graphs of f and g. Show clearly on your graphs the turning points and asymptotes, if any. (6)
6.2 Write down the period of f. (2)
6.3 For what values of x is f(x). g(x) < 0 for x ∈ [−90°; 120°]? (2)
6.4 Write down the equation(s) of the asymptotes of h if ℎ(x) = f(x + 10°) for x ∈ [−90°; 180°] (1)
[11]
QUESTION 7
In the diagram below, ABCD is a quadrilateral with diagonal AC drawn.
AB = BC = 17 m
AD = 13 m
D̂ = 75°
B̂ = 105° 
Calculate:
7.1 The area of △ ABC. (3)
7.2 The length of AC. (3)
7.3 The size of AĈD. (3)
7.4 Give a reason why ABCD is a cyclic quadrilateral. (1)
[10]
Give reasons for ALL statements in QUESTION 8, 9, 10 AND 11.
QUESTION 8
8.1 PR is a diameter of the circle PRSU. QU is drawn parallel to RS and meets SP in T.
8.1.1 Write down, with a reason, the size of Ŝ. (2)
8.1.2 If the diameter is 20 cm and SP = 16 cm, calculate the length of TU. (6)
8.2 ABC is a tangent to circle BPQRS at B. PQ ∥ BS. QR = RS. Ŝ1 = 30° and B̂3 = 70°. 
Calculate, with reasons, the size of the following angles:
8.2.1 B̂1(2)
8.2.2 P̂2(2)
8.2.3 R̂ (2)
8.2.4 Q̂2(3)
[17]
QUESTION 9
9.1 A, B and P are the points on the circle with centre O. AO, BO, AP and BP are drawn. 
Prove the theorem which states that AÔB = 2AP̂B. (4)
9.2 TV and VU are tangents to the circle with centre O at T and U respectively. TSRUY are points on the circle such that RT is the diameter. X is the midpoint of chord TU. T̂3 = y. 
Prove that:
9.2.1 RU ∥ SY (5)
9.2.2 T̂1=½y (5)
9.2.3 TOUV is a cyclic quadrilateral (5)
[19]
QUESTION 10
In the diagram below, D and E are points on sides AC and AB respectively of △ ABC such that DE ∥ BC. F is a point on BC such that EF ∥ AC. AB produced and DF produced meet in G. 
10.1 Prove that: BC = AC
FC DA(4)
10.2 Prove that: Δ BFE ||| Δ EDA(3)
10.3 It is further given that EF = 2, BF = 3,5 and ED = 10, determine the length of:
10.3.1 AD (4)
10.3.2 DC (2)
[13]
TOTAL: 150
